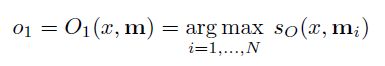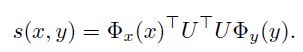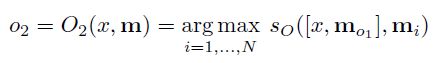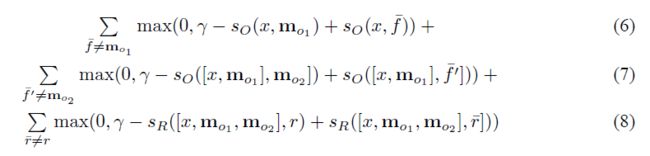论文|记忆网络之Memory Networks
欢迎直接到我的博客查看最近文章:www.pkudodo.com。更新会比较快,评论回复我也能比较快看见,排版也会更好一点。
原始blog链接: http://www.pkudodo.com/2019/06/14/1-13/
Memory NetWorks介绍
在文本的处理上,由于很多地方对记忆的需要,因此诞生了RNN及LSTM。但RNN和LSTM也只能用于短时间内的记忆(一般来说也就十几个step)。所以如果文本较长的话,RNN和LSTM也无能为力了。
当然也有一种方法,就是直接扩大RNN和LSTM的隐状态大小,让其可以存储更多的信息。但相对于这种方式,我们更希望能够任意地增加记忆量,同时能够对模型做尽可能小的改变。
Memory Networks正是从这一角度出发得到的产物。直观来讲,Memory Networks可以理解成正常的model额外加一个记忆模块。
就好像我们使用的CPU(普通的model),它内部是有一个很小的ram的(我本科阶段是嵌入式方向,目前见过cpu内部最小的ram只是kb的量级),但如果要运行操作系统或软件的话,内部ram就不够了(memory不够),所以通常会外扩一个ram芯片(Memory Networks),这样cpu的运行并没有什么改变,只不过在需要memory来配合推理的时候,直接从Memory Networks中存取就可以了。
memory network在提出后又经历了几次变体,这次先写《memory networks》,这是memory networks被facebook首次提出的原始论文。后续又经历了几次变体。下一篇就会讲它end-to-end 的memory network,这是对于原始MemNN的一次改进。
《Memory Networks》
Memory Networks一共有5个部分,分别是memory m、I、G、O、R,其中
memory m:m由一系列的mi组成,其中mi是单个向量,每个mi都表示某一个方面的记忆存储。当要更新记忆的时候,就操作使用新记忆去更新相应的mi,要写入记忆时直接写入mi即可。至于i的范围则依据实际的使用策略不同而作相应的修改。
I:输入特征映射,它负责将输入转换成内部的特征表示形式。比如说输入的是文本,就需要它将其转换成model可以看懂的数学形式(比如说word转换成embedding形式、文本转换成向量等),也可以认为是数据的预处理的一个过程。用I(x)表示运算过程,其中x是输入。
G:更新记忆,根据当前的memory状态(m)、当前的输入(I(x))、要更新的记忆(mi),得到更新后的记忆,并更新mi。用mi=G(mi, I(x), m)表示,其中i为m的数目范围内的任意数,具体怎么指定i的值,后续会解释。
O:输出映射,根据当前的记忆状态以及当前的输入,确定当前的输出,但输出是内部特征表示形式(比如说一个稠密的向量),因此还需要一个步骤作转换。用o=O(I(x), m)表示。
R:回应,负责将O步骤输出的o转换成系统交互的形式,例如文本或系统动作。用r=R(o)表示,最简单的理解就是把o输入一个rnn,使用seq2seq或者类似的结构输出对应的文本或动作即可。
一个文本的例子——最基本的模型应用
怎么把数据存到memory
最简单的一个方法就是顺序存,比如说定义有n个m,即mi中i的取值范围为0-999。那么每次要往memory存的时候,就找到下一个空着的memory,将输入x原封不动地放进去(这是最简单的策略,比如说x是个句子,就把句子直接放到memory中),之后N+1,下次就会往下一个memory存。
![]() 由于G是负责更新memory的,所以在这种策略中,G只是很简单的原封不动地输出x。
由于G是负责更新memory的,所以在这种策略中,G只是很简单的原封不动地输出x。
怎么提取指定记忆
那么存记忆已经搞定了,另一个主要的问题是取记忆,比如说下面这段小故事:
- Joe去了厨房。
- Fred去了厨房。
- Joe拿起了牛奶。
- Joe去了办公室。
- Joe放下了牛奶。
- Joe上了厕所。
提问:牛奶现在在哪里?
一共6句话,根据当前的存储策略,6句话直接以原始形式存在了m中,这个时候根据提问怎么知道哪句话是和提问相关的呢?
如果我们自己做这个题,就会把每个句子再看一遍,定位到了第五句——Joe放下了牛奶。memory network做的也是这件事情,它使用了O模块,去计算当前输入x和每一个m的相关程度,找到最相关的句子mi,公式如下:
其中so是一类计算相关程度的函数,它最后会输出一个得分,x和所有的m遍历计算,直到找到得分最高的即为最相关的句子i。
其中score函数如下:
U的大小为[n,D],Φx和Φy是D维向量,Φ(x)负责将x映射到内部向量表示形式(比如说最简单的就是词袋模型)。所以最后的s(x,y)的结果是一个实数,表示了分数。
但是这其中存在一个问题,比如说我们找到了最相关的i是5,放下了牛奶,但牛奶在哪里我们仍然不知道。所以对于人来说,会往前看一句,发现第4句“Joe去了办公室”直接暗示了牛奶在办公室。第4句和第5句结合才能得到牛奶在办公室的答案。
因此不光要找到最相关的句子,还应该找到第二相关的句子(paper中用k来定义一共找前k个相关的句子,这里k=2)。
值得注意的是,并不是简单地找到前2个相关句子,在找第2个句子时,需要以找到的第一个句子为条件。像上面的式子中,需要以x和m01为条件去找mo2。作者没有提到这么做的原因,但我认为是为了能够在有了第一个句子的情况下,再去找到一个另外的能够有最强代表性的句子,而不是说两个句子其实指代的是同一个方面,这样跟找一个句子也没什么差别。
输出
在这个例子中,输出并不要求是字符串,只要一个word即可,比如说“办公室”(这里引用的是原文中的例子,在英文中是单个的“office”,如果是中文情况下,可以加一个rnn来生成字符串)。
所以输出函数的输入是当前输入、m01,m02和字典,输出是字典当中最有可能的那个单词,公式如下:
训练
k=2时的目标函数如下:
(6)表示挑出来的句子是否是正确的句子,(7)表示在第一个句子被正确挑出来的情况下,第二个句子是否是正确的句子。(8)最后输出的是否是正确的答案。
可以看到loss其实对train的各个方面都做了一个约束,最后的performance效果也是非常好。
其他
论文的后半部分补充了很多小技巧,例如memory如果非常大的解决方法、遇到新词等。这里就不再过多展开了。