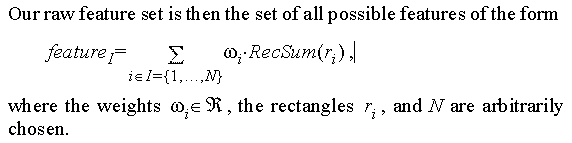特征提取之——Haar特征
本文有自己的原创,也有转载摘录的文章,转载部分在这里这里这里等等。
特征提取方法有很多种,比如说Haar特征,edgelet特征,shapelet特征,HOG特征,HOF特征,小波特征,边缘模板等等
Haar特征最开始源自Papageorgiou的文章 这里 A general framework for object detection
P. Viola and M. Jones.在此基础上,使用3种类型4种形式的特征。论文:
P. Viola and M. Jones. Rapid object detection using a boosted cascade of simple features.
Rainer Lienhart和Jochen Maydt用对角特征,即Haar-like特征对检测器进行了扩展,论文如下:
R. Lienhart and J. Maydt. An Extended Set of Haar-like Features for Rapid Object Detection.
OpenCV中参考文献中自带的人脸检测算法即基于此检测器,称为“Haar分类器”。引用自这里
确切地说:
Haar分类器 = Haar-like特征 + 积分图方法 + AdaBoost +级联
所以,先学习Haar-like特征
2001年,Viola和Jones两位大牛发表了经典的《Rapid Object Detection using a Boosted Cascade of Simple Features》和《Robust Real-Time Face Detection》,在AdaBoost算法的基础上,使用Haar-like小波特征和积分图方法进行人脸检测,他俩不是最早使用提出小波特征的,但是他们设计了针对人脸检测更有效的特征,并对AdaBoost训练出的强分类器进行级联。这可以说是人脸检测史上里程碑式的一笔了,也因此当时提出的这个算法被称为Viola-Jones检测器。又过了一段时间,Rainer Lienhart和Jochen Maydt两位大牛将这个检测器进行了扩展,最终形成了OpenCV现在的Haar分类器。
Haar分类器算法的要点如下:
① 使用Haar-like特征做检测。
② 使用积分图(Integral Image)对Haar-like特征求值进行加速。
③ 使用AdaBoost算法训练区分人脸和非人脸的强分类器。
④ 使用筛选式级联把强分类器级联到一起,提高准确率。
本文重点讲 Haar-like特征Papageorgiou等提出的只有三种特征
P. Viola and M. Jones等增加了Line features等等
接着是R. Lienhart and J. Maydt等
综上,这些Haar特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。
特征模板内有白色和黑色两种矩形,定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况。
例如:脸部的一些特征能由矩形特征简单的描述,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构,如边缘、线段较敏感,所以只能描述特定走向(水平、垂直、对角)的结构。如下图所示:
上图中两个矩形特征,表示出人脸的某些特征。比如中间一幅表示眼睛区域的颜色比脸颊区域的颜色深,右边一幅表示鼻梁两侧比鼻梁的颜色要深。同样,其他目标,如眼睛等,也可以用一些矩形特征来表示。使用特征比单纯地使用像素点具有很大的优越性,并且速度更快。
在给定有限的数据情况下,基于特征的检测能够编码特定区域的状态,而且基于特征的系统比基于象素的系统要快得多。
在给定有限的数据情况下,基于特征的检测能够编码特定区域的状态,而且基于特征的系统比基于象素的系统要快得多。
矩形特征对一些简单的图形结构,比如边缘、线段,比较敏感,但是其只能描述特定走向(水平、垂直、对角)的结构,因此比较粗略。如上图,脸部一些特征能够由矩形特征简单地描绘,例如,通常,眼睛要比脸颊颜色更深;鼻梁两侧要比鼻梁颜色要深;嘴巴要比周围颜色更深。
常用的矩形特征有三种:两矩形特征、三矩形特征、四矩形特征,如图:
![]()
由图表可以看出,两矩形特征反映的是边缘特征,三矩形特征反映的是线性特征、四矩形特征反映的是特定方向特征。
特征模板的特征值定义为:白色矩形像素和减去黑色矩形像素和。
现在的关键问题是1:求出每个待检测子窗口中的特征个数。2:求出每个特征的特征值。
子窗口中的特征个数即为特征矩形的个数。训练时,将每一个特征在训练图像子窗口中进行滑动计算,获取各个位置的各类矩形特征。在子窗口中位于不同位置的同一类型矩形特征,属于不同的特征。可以证明,在确定了特征的形式之后,矩形特征的数量只与子窗口的大小有关。在24×24的检测窗口中,矩形特征的数量约为160,000个。
特征模板可以在子窗口内以“任意”尺寸“任意”放置,每一种形态称为一个特征。找出子窗口所有特征,是进行弱分类训练的基础。
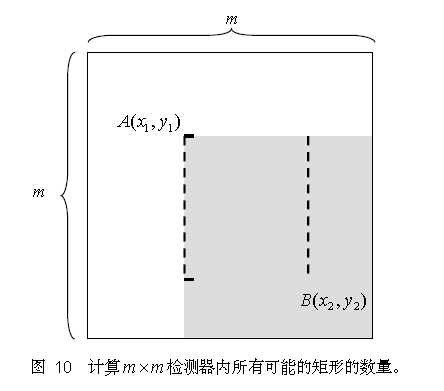
子窗口内的条件矩形以 m×m 像素分辨率的检测器为例,其内部存在的满足特定条件的所有矩形的总数可以这样计算:
对于 m×m 子窗口,我们只需要确定了矩形左上顶点 A(x1,y1) 和右下顶点(B(x2,y2),即可以确定一个矩形;如果这个矩形还必须满足下面两个条件(称为
(s, t)条件,满足(s, t)条件的矩形称为条件矩形):
1) x 方向边长必须能被自然数s 整除(能均等分成s 段);
2) y 方向边长必须能被自然数t 整除(能均等分成t 段);
则 , 这个矩形的最小尺寸为s×t 或t×s, 最大尺寸为[m/s]·s×[m/t]·t 或[m/t]·t×[m/s]·s;其中[ ]为取整运算符。
条件矩形的数量
我们通过下面两步就可以定位一个满足条件的矩形:
![]()
由上分析可知,在m×m 子窗口中,满足(s, t)条件的所有矩形的数量为:
![]()
实际上,(s, t)条件描述了矩形特征的特征,下面列出了不同矩形特征对应的(s, t)条件:
![]()
![]()
下面以 24×24 子窗口为例,具体计算其特征总数量:
![]()
下面列出了,在不同子窗口大小内,特征的总数量:
![]()
每个特征由2~3个矩形组成,在这些小波示意图中,白色区域表示“累加数据”,黑色区域表示“减去该区域的数据”。
分别检测边界、线、中心特征,这些特征可表示为:
其中wi表示矩形的权重,RectSum(ri) 为矩形 ri 所围图像的灰度积分, N 是组成 featurej 的矩形个数。