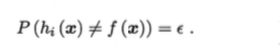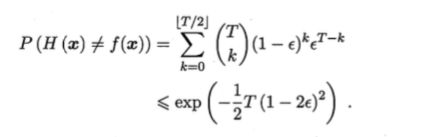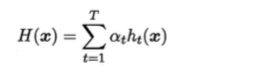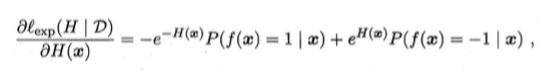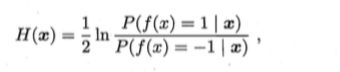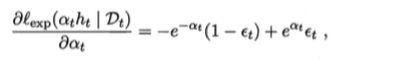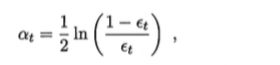Adaboost 算法
本文结构:
- 什么是集成学习?
- 为什么集成的效果就会好于单个学习器?
- 如何生成个体学习器?
- 什么是 Boosting?
- Adaboost 算法?
什么是集成学习
集成学习就是将多个弱的学习器结合起来组成一个强的学习器。
这就涉及到,先产生一组‘个体学习器’,再用一个策略将它们结合起来。
个体学习器可以选择:决策树,神经网络。
集成时可以所有个体学习器属于同一类算法:全是决策树,或全是神经网络;也可以来自不同的算法。
结合策略:例如分类问题,可以用投票法,少数服从多数。
之所以用这种集成的思想,是因为单独用一个算法时,效果往往不容易达到很好,但如果多个个体算法结合在一起,取长补短,整体效果就会比单独一个要强。
什么时候集成的效果就会好于单个学习器
当然集成并不是不管怎么选择学习器,怎么组合都一定会获得更好的效果,最好的情况是,每个学习器都不是特别差,并且要具有一定的多样性,否则可能集成后的会没有效果,或者起负作用:
来证明一下:
假设个体学习器的错误率为 ε,
假设错误率相互独立,由 Hoeffding 不等式可得到整体学习器的错误率为:
由不等式的右边可知,如果将学习器的数目 T 逐渐增大,那么整个学习器的错误率将指数级下降,甚至最终趋向于零。
这里提到了‘错误率相互独立’的假设,这就是集成学习的一个核心问题:
如何生成准确性又不是很差,并且还能保证多样性的个体学习器呢
目前主要有两种生成方式:
Boosting:个体学习器间存在强依赖关系,必须串行生成。
Bagging,随机森林:个体之间不存在强依赖关系,可并行生成。
Boosting 思想:
给定初始训练数据,由此训练出第一个基学习器;
根据基学习器的表现对样本进行调整,在之前学习器做错的样本上投入更多关注;
用调整后的样本,训练下一个基学习器;
重复上述过程 T 次,将 T 个学习器加权结合。
根据 Boosting 的定义,它有三个基本要素:
基学习器
组合方式
目标函数
Boosting 的代表是 Adaboost:
AdaBoost方法相对于大多数其它学习算法而言,不会很容易出现过拟合现象。
Adaboost 算法
第 1 行,初始化样本权重分布,此时每个数据的权重是一样的,所以是 1/m;
以分类问题为例,最初令每个样本的权重都相等,对于第 t 次迭代操作,我们就根据这些权重来选取样本点,进而训练分类器C_t。第 2 行,进入 for 循环 T 次,即基学习器的个数为 T 个;
第 3 行,根据具有当前权重分布
D_t的数据集,学习出h_t;
前一个分类器分错的样本会被用来训练下一个分类器。
h_t是分量分类器C_t给出的对任一样本点 xi 的标记(+1或-1),h_t(xi) = yi时,样本被正确分类。第 4 行,计算当前学习器的误差;
第 5 行,如果误差大于 0.5,就停止;
AdaBoost 方法中使用的分类器可能很弱(比如出现很大错误率),但只要它的分类效果比随机好一点(比如两类问题分类错误率略小于0.5),就能够改善最终得到的模型。第 6 行,计算当前学习器的权重
α_t;
权值是关于误差的表达式,当下一次分类器再次错分这些点之后,会提高整体的错误率,这样就导致分类器权值变小,进而导致这个分类器在最终的混合分类器中的权值变小,也就是说,Adaboost算法让正确率高的分类器占整体的权值更高,让正确率低的分类器权值更低,从而提高最终分类器的正确率。第 7 行,得到下一时刻的权重分布
D_t+1.
如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它被选中的概率就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。通过这样的方式,AdaBoost 方法能“聚焦于”那些较难分(更富信息)的样本上。
最后的总体分类的判决可以使用各个分量分类器加权平均来得到,
再取符号,这样,最后对分类结果的判定规则是:
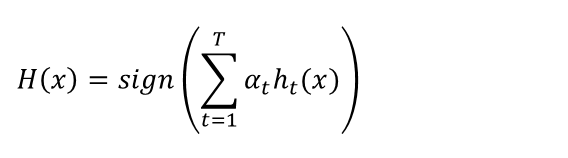
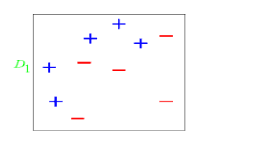
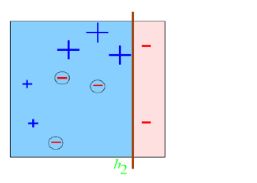
举个例子
图中“+”和“-”表示两种类别,
共10个样本,故每个样本权值为0.1,
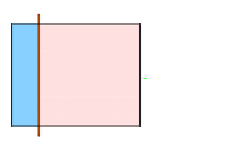
第一次划分有3个点划分错误,根据误差表达式得到误差:e1=(0.1+0.1+0.1)/1.0=0.3
分类器权重:
根据算法,对于正确分类的7个点,权值不变,仍为0.1, 对于错分的3个点,权值为:
D1=D0*(1-e1)/e1=0.1*(1-0.3)/0.3=0.2333
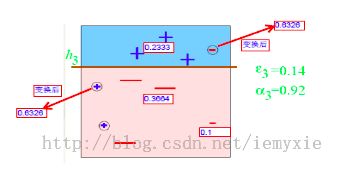
第二次分类,有3个 “-” 分类错误,按照算法计算如下:
上轮分类后权值之和为:0.17+0.23333=1.3990
分类误差:e2=0.1*3/1.3990=0.2144
分类器权重 a2=0.6493
错分的3个点权值为:D2=0.1*(1-0.2144)/0.2144=0.3664
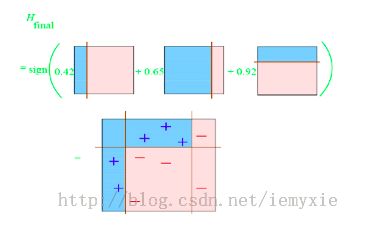
第三次:
接下来看 α_t , D_t 是怎么推导出来的
我们最后学习出来的预测数据的模型为 H:
即强学习器是基学习器的线性组合形式。
目标函数用指数损失函数:
为什么目标函数用指数损失函数?
当我们用指数损失函数时,
我们需要求得 H 使得损失函数达到极小,那么就想到求偏导,
并使其为 0,得到 H 的形式:
那么最终的判定规则为:
说明若指数损失达到最小,则分类错误率也将最小化,也就是说指数损失可以作为分类任务 0 1 损失的替代函数,因为它连续可微,就用它来替代 0 1 损失函数作为优化目标。
第一个基学习器由初始数据得到,之后的 α_t , h_t 都是迭代产生。
第 6 行: α_t
想要求得 α_t 使得 α_t*h_t 最小化指数损失函数:
那就需要对 α_t 求导:
使导数为 0 后得到 α_t 的解为:
第 4,5 行: h_t 的条件
学习到 H_t-1 后,希望下一个 h_t 可以纠正 H_t-1 的全部错误,即使下面的目标函数达到最小:
经过一系列推导后,可得到理想的基学习器为:
即理想的 h_t 将在分布 D_t 下最小化分类误差,也就是在用 D_t 训练 h_t 时,分类误差应小于 0.5。
第 7 行:再推导一下 D_t 和 D_t-1 之间的关系
这样就推导出了 Adaboost 算法。
参考:
《机器学习》
https://zh.wikipedia.org/wiki/AdaBoost
http://blog.csdn.net/iemyxie/article/details/40423907
推荐阅读
历史技术博文链接汇总
也许可以找到你想要的