2020年全国大学生数学建模竞赛ABC题怎么分析？

至少花两个小时用来确定题目。
A 题 炉温曲线
B 题 穿越沙漠
C 题 中小微企业的信贷决策

一贯继承我之前的风格，在这里和大家分享一下我的题目剖析结果。

仔细看了一下ABC三道题，A题是热力学仿真方向的题目，其本质是优化问题，B题也可以看作是优化的题目，至少第一问是这样，后面的题目涉及到博弈心理方面的知识，C题是常见的信贷决策类大数据分析题目。

依据开放性由大到小进行排序：C>B>A。C题最终的目标是给出合理的信贷策略，这个策略是依据数据分析结果合理给出的即可。B题除第一问要求玩家最佳策略及最终结果外，之后的每一问只要求给出最佳策略和具体讨论，这里的讨论就有很大的发挥空间。A题延续了以往优化题目的有合理答案区间的特点，故而开放性最小。

依据难易度偏好由低到高进行选题：C>A>B。可以肯定，这次选C题的人必然最多，因为C题是常规题型，且较为简单。其次是A题，虽然A题是物理热力学与优化问题的结合，但只需查阅几篇文献对热量传递有所了解，就可以通过假设将这个问题转化为完全的数学优化问题，从而进行求解。B题可能在一部分人看起来挺简单的，但随着题目的深入，便会发现其不如表面表现得那么有趣和人畜无害，其涉及到图论求最短路径，背包问题，博弈论等诸多方面。

依据我的兴趣由高到低进行选题：B>A>C。这次的B题让我想起了去年国赛的多人颠小球问题，同样都是这样有趣，甚至这次的B题更加有趣，因为游戏设计是我挺感兴趣的一个方面，如有同好，可以考虑选这道题。A题涉及物理热力学方面，因为在之前的比赛中总是没选过这类题（油罐散热、浴缸保温），所以好想尝试一下的，嘿嘿。C题嘛，这类题之前做过不少，兴趣乏乏。

下面逐题进行分析：

C题 中小微企业的信贷决策

**背景：**中小微企业规模相对较小，也缺少抵押资产，因此银行通常是依据信贷政策、企业的交易票据信息和上下游企业的影响力，向实力强、供求关系稳定的企业提供贷款，并可以对信誉高、信贷风险小的企业给予利率优惠。银行首先根据中小微企业的实力、信誉对其信贷风险做出评估，然后依据信贷风险等因素来确定是否放贷及贷款额度、利率和期限等信贷策略。

数据分析题最重要的就是观察数据、理解数据，而后再动手解题。

问题 1： 对123家企业的信贷风险进行量化分析，给出该银行在年度信贷总额固定时对这些企业的信贷策略。

**思路：**查看附件1发现有3个表格，分别是企业信息、进项发票、销项发票。如何对信贷风险进行量化分析，其实在题目中已经指出了方向——“根据中小微企业的实力、信誉”做出评估。实力由企业的交易票据信息和上下游企业的影响力体现，信誉由信誉评级体现。此时可以给出银行的信贷策略。

**问题 2：**在问题1的基础上，对302家企业的信贷风险进行量化分析，并给出该银行在年度信贷总额为1亿元时对这些企业的信贷策略。

思路：这里需要解决的问题是302家企业无信贷记录，自然无信誉评级，那么企业的信誉如何刻划？或者说信贷风险是否采取不一样的量化方式，取消信誉评级所占比重。这个问题解决了，问题二就解决了。

问题 3：综合考虑附件2中各企业的信贷风险和可能的突发因素对各企业的影响，给出该银行在年度信贷总额为1亿元时的信贷调整策略。

**思路：**此问的关键是找到指标来刻划企业抵御突发因素影响的能力，将其纳入到信贷风险评价体系中，重新确定信贷策略。

B题 穿越沙漠

**背景：**小游戏，玩家凭借一张地图，利用初始资金购买一定数量的水和食物（包括食品和其他日常用品），从起点出发，在沙漠中行走。途中会遇到不同的天气，也可在矿山、村庄补充资金或资源，目标是在规定时间内到达终点，并保留尽可能多的资金。有8条游戏的基本规则。需要根据游戏的不同设定，建立数学模型，解决问题。

这个题目看着着实有趣，但细细思来，所需要考虑的多种因素相互制约，需要共同优化才能求的满意的结果，整体难的还是偏高的。但也不用怕，建模也不是必须做到最完美才能获得最高奖项，比大多数好即可。

在背景中的“目标”二字我进行了加粗，因为这个是B题所有问题的最高要求。做B题，我们需要仔细研究8条基本规则，根据规则来对做出能保留尽可能多的资金的决策。

问题 1： 假设只有一名玩家，在整个游戏时段内每天天气状况事先全部已知，试给出一般情况下玩家的最优策略。求解附件中的“第一关”和“第二关”，并将相应结果分别填入Result.xlsx。

**思路：**就第一问而言，首先需要将地图用散列矩阵的方式表示出任意两个区域之间是否相邻，且最短的路程需要跨越几次边界。其次需要计算出直接向终点出发、先去矿山采矿去村庄购物再向终点出发等多种方案的最终剩余资金。最后对不同方案的剩余资金进行比较，选择剩余资金最多的方案，存入Result.xlsx中。

**问题 2：**假设只有一名玩家，玩家仅知道当天的天气状况，可据此决定当天的行动方案，试给出一般情况下玩家的最佳策略，并对附件中的“第三关”和“第四关”进行具体讨论。

**思路：**这里提到了“一般情况”，在附件中提到，第三关，玩家仅知道当天的天气状况，但已知10天内不会出现沙暴天气。第四关，玩家仅知道当天的天气状况，但已知30天内较少出现沙暴天气。此时可以按照问题一的方法确定多种方案，通过每种方案所走路线和天数，而后倒推出在之后每一天都是高温天气情况下，出发时应该购买的水和食物。而后计算出到终点后的最终剩余资金，进行比较，给出最佳策略。

问题 3：现有n名玩家，他们有相同的初始资金，且同时从起点出发。若某天其中的任意k名玩家均从区域A行走到区域B，则他们中的任一位消耗的资源数量均为基础消耗量的2*k倍；若某天其中的任意k名玩家在同一矿山挖矿，则他们中的任一位消耗的资源数量均为基础消耗量的3倍，且每名玩家一天可通过挖矿获得的资金是基础收益的1/k；若某天其中的任意k名玩家在同一村庄购买资源，每箱价格均为基准价格的4倍。其他情况下消耗资源数量与资源价格与单人游戏相同。

（1）假设在整个游戏时段内每天天气状况事先全部已知，每名玩家的行动方案需在第0天确定且此后不能更改。试给出一般情况下玩家应采取的策略，并对附件中的“第五关”进行具体讨论。

**思路：**第五关n=2，在问题三中，要求行动方案需提前设定好，增加了玩家“同行”时的消耗，降低了玩家“同挖”时的收益，提高了玩家“同买”时的价格。这就要求玩家们在设定行动方案时要尽量避免与其他玩家相遇。这里的关键是“猜”其他玩家的心理，这就是博弈论。

（2）假设所有玩家仅知道当天的天气状况，从第1天起，每名玩家在当天行动结束后均知道其余玩家当天的行动方案和剩余的资源数量，随后确定各自第二天的行动方案。试给出一般情况下玩家应采取的策略，并1对附件中的“第六关”进行具体讨论。

思路：这一小问不再要求行动方案需提前设定好，而是每一天结束都可以知道所有玩家的这一天的行动方案和资源数量。这就使得需要使用每天的动态数据预测其他玩家第二天的行动方案。从而在不与其他玩家相遇的可行方案中，挑选出最终剩余资金期望最高的第二天的行动方案。而后逐日迭代。

A题 炉温曲线

背景：电子产品生产中，需要将安装有各种电子元件的印刷电路板放置在回焊炉中，通过加热，将电子元件自动焊接到电路板上。让回焊炉的各部分保持工艺要求的温度，对产品质量至关重要。目前，这方面的许多工作是通过实验测试来进行控制和调整的。本题旨在通过机理模型来进行分析研究。

**机理模型，**亦称白箱模型。根据对象、生产过程的内部机制或者物质流的传递机理建立起来的精确数学模型。

仔细阅读题目，摄取关键的信息和数据指标。

1、回焊炉分4个大温区（预热区、恒温区、回流区、冷却区），11个小温区。进入回焊炉的传送带为匀速。并给出每个小温区长度为30.5cm，相邻小温区之间有5cm的间隙，炉前区域和炉后区域长度均为25cm。

2、炉内空气温度会在短时间内达到稳定，故假设开始加工时炉内空气温度稳定。

3、通过温度传感器测试某些位置上焊接区域中心的温度，称之为炉温曲线。传感器在焊接区域中心的温度达到30ºC时开始工作，电路板进入回焊炉开始计时。给出了一次实验中的小温区温度、传送带速度、焊接区域厚度的数据。

4、各小温区设定温度可以进行10ºC范围内的调整。调整时要求小温区1~ 5中的温度保持一致，小温区8~ 9中的温度保持一致，小温区10 ~ 11中的温度保持25ºC。传送带的过炉速度调节范围为65~100 cm/min。

5、给出了制程界限，即在回焊炉电路板焊接生产中，炉温曲线应满足一定的要求。

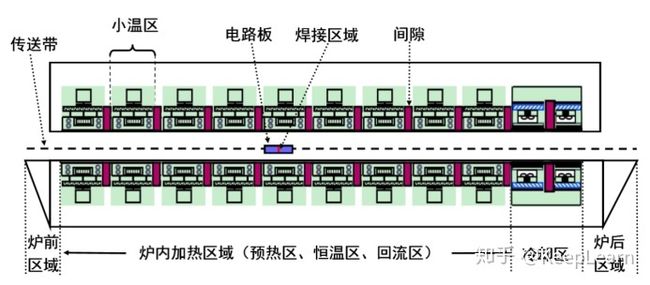
图1 回焊炉截面图

问题 1： 请对焊接区域的温度变化规律建立数学模型。假设传送带过炉速度为78 cm/min，各温区温度的设定值分别为173ºC（小温区1~ 5）、 198ºC （小温区6）、 230ºC（小温区7）和257ºC（小温区8~ 9），请给出焊接区域中心的温度变化情况，列出小温区3、6、7中点及小温区8结束处焊接区域中心的温度，画出相应的炉温曲线，并将每隔0.5 s焊接区域中心的温度存放在提供的result.csv中。

**思路：**题中给出一次实验的设定数据及在设定条件下对电路板中心测温的炉温曲线数据。首先通过热力学知识，将回焊炉的设定数据转变为在传送带上的温度分布曲线，而后与电路板加工时温度变化的曲线进行对应，找出温差与电路板温度变化的规律。之后对问题1中的设定数据求解传送带上的温度分布曲线，应用前述规律对电路板焊接区域中心的温度进行逆向求解。

**问题 2：**假设各温区温度的设定值分别为182ºC（小温区1~ 5）、203ºC（小温区6）、237ºC（小温区7）、 254ºC（小温区8~9），请确定允许的最大传送带过炉速度。

**思路：**与问题1不同，这里是已知制程界限，即已知炉温曲线需要满足的条件，而后找到可以满足最低条件的最大传送带速度。这里可以先分析满足加工条件的最低炉温曲线，而后应用热力学知识对升、降温速度进行求解，进而求得最大过炉速度。

**问题 3：**在焊接过程中，焊接区域中心的温度超过217ºC的时间不宜过长，峰值温度也不宜过高。理想的炉温曲线应使超过217ºC到峰值温度所覆盖的面积（图2中阴影部分）最小。请确定在此要求下的最优炉温曲线，以及各温区的设定温度和传送带的过炉速度，并给出相应的面积。图2 炉温曲线示意图

**思路：**要求超过217ºC的炉温曲线覆盖面积最小，首先限制在217ºC以上的时间为最小值，而后分析各小温区温度对峰值温度的影响，尽量使得温度尽快到达240~250ºC之间，而后尽快降温。此时的阴影部分面积最小，此时的炉温曲线即为所求。

**问题 4：**在焊接过程中，除满足制程界限外，还希望以峰值温度为中心线的两侧超过217ºC的炉温曲线应尽量对称（参见图2）。请结合问题3，进一步给出最优炉温曲线，以及各温区设定的温度及传送带过炉速度，并给出相应的指标值。

**思路：**要求以峰值温度为中心线的两侧超过217ºC的炉温曲线应尽量对称，分析可得，即要求在峰值温度两侧的升、降温速度尽量一致。升降温速度与两点之间温度差有关，所以等同于要求传送带上的温度分布曲线在峰值温度对应的时间附近对称。最后通过热力学知识，将传送带上的温度分布曲线转变为回焊炉的设定数据。

点击上面，然后回复2020数学建模领取本题必用工具，你懂的！！