lingo入门——河北省第三届研究生建模竞赛B题
一、题干
1.1 题目
投资建模(河北省第三届研究生建模竞赛B题)
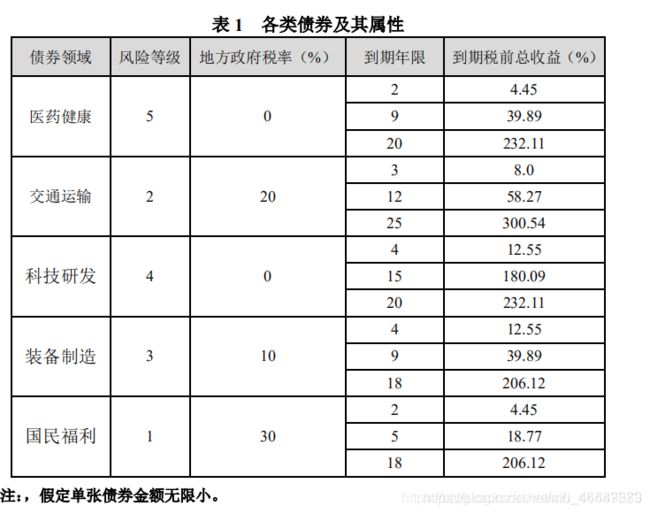
从2021年年初开始到2050年前,未来教育基金会(FFE)向M国部分高等院校捐助一笔经费以帮助贫困学生,将现有的8000万美元资金进行债务投资。
相关投资要求:
- 医药健康债券购买金额不能少于购买总金额的20%,交通运输、科技研发、装备制造以及国民福利的债券购买金额不能少于购买总金额的10%。
- 所购买债券的平均风险等级不得低于2.5,等级数字越大,风险越低。
- 所购买的债券的平均到期年限不超过10年。
- 要求捐助活动结束后FFE继续保留8000万美元资金。
如上所示为各个基金的一些信息,值得注意的是,其对风险等级的约束很小,而收益率又定义为固定值,所以这个模型相对实际问题已经做了很大的简化。
1.2 问题
- 若 SEB 债券投资只允许在第一年初进行,分配8000万美元使收益最大。
- 假定可以进行重复投资,使得 2050 年末的一次性捐款金额达到最大。
- FFE 改变捐助方式,计划从 2021 开始,在未来 30 年内每年年初捐助一笔每年金额固定的经费。允许重复投资。使得每年捐助的金额达到最大。
- FFE 为了帮助疫情防控,决定在每年捐助给高校的金额尽量不低于第 3 问 的金额的前提下,投资尽量向医药健康和科技研发上倾斜。原则上规定:医药健康的投资额,尽量与科技研发相等,尽量是交通运输的 1.2 倍,尽量是装备制造 的 1.5 倍,尽量是国民福利的 2 倍。允许重复投资。
二、模型的建立
第一问没啥写的价值,直接写第二、三、四问。
2.1 符号
| 符号 | 意义 |
|---|---|
| m o n e y _ i n i money\_in_i money_ini | 第 i i i年在收入状态后的总资金 |
| m o n e y _ o u t i money\_out_i money_outi | 第 i i i年在支出状态后的总资金 |
| x i , j x_{i,j} xi,j | 第 i i i年对第 j j j个债券的购买量 |
| a i a_i ai | 第 i i i个产品在一轮周期后的利润率 |
| b i b_i bi | 第 i i i个产品一轮周期时常 |
| c i c_i ci | 第 i i i个产品增值税率 |
| d i d_i di | 第 i i i个产品风险等级 |
| p p p | 每年的捐款数量 |
2.2、思路
2.2.1、思路1
观察这道题目在投资时的资金流转过程,可以发现它每年都有这么两组操作:
- 继承一年剩下的资产、获取前几年投资所带来的利润
- 进行各类债券进行投资、对外捐赠(第三问)
所以我们可以考虑对该问约束时进行状态分离,即先进行 m o n e y i n i moneyin_i moneyini操作,再进行 m o n e y o u t i moneyout_i moneyouti操作。其间的等量关系大致如下,其他的具体情况在正式做的时候再具体讨论:
m o n e y _ i n i = m o n e y _ o u t i − 1 + ∑ j = 1 15 [ x i − b i , j + x i − b i , j a i ( 1 − c i ) ] m o n e y _ i n i = m o n e y _ o u t i + p + ∑ j = 1 15 x i , j money\_in_i=money\_out_{i-1}+\sum_{j=1}^{15}{[x_{i-b_i,j}+x_{i-b_i,j}a_i(1-c_i)]}\\ money\_in_i=money\_out_i+p+\sum_{j=1}^{15}{x_{i,j}} money_ini=money_outi−1+j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]money_ini=money_outi+p+j=1∑15xi,j
2.2.2、思路2
首先根据一个很明显的构想:如果你当下有钱,且时间足够充裕到你得到收益,那么你必然会去拿这笔钱去投资。甭管投啥,反正会投(而投啥其实就是我们要去求解的内容)。因为如果你今年不投,今后再投的话,在收益上除了时间线的后移外没有任何变化。所以这里本质上是一个带约束的贪心问题。
我们可以粗略的建立一个等量关系,其他的具体情况在正式做的时候再具体讨论:
∑ j = 1 15 x i , j = ∑ j = 1 15 [ x i − b i , j + x i − b i , j a i ( 1 − c i ) ] \sum_{j=1}^{15}{x_{i,j}}=\sum_{j=1}^{15}{[x_{i-b_i,j}+x_{i-b_i,j}a_i(1-c_i)]} j=1∑15xi,j=j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]
2.3 确定等量关系
思考了上面两个思路后,发现他们本身其实是并不冲突的,但问题在于以上的贪心算法并没有考虑留每天的捐款的情况。只是表现的形式不一样。所以可以将他们结合起来,建立如下等量关系。
{ m o n e y _ i n i = m o n e y _ o u t i − 1 + ∑ j = 1 15 [ x i − b i , j + x i − b i , j a i ( 1 − c i ) ] m o n e y _ i n i = m o n e y _ o u t i + p + ∑ j = 1 15 x i , j \begin{cases} money\_in_i=money\_out_{i-1}+\sum\limits_{j=1}^{15}{[x_{i-b_i,j}+x_{i-b_i,j}a_i(1-c_i)]}\\ money\_in_i=money\_out_i+p+\sum\limits_{j=1}^{15}{x_{i,j}}\\ % p+\sum\limits_{j=1}^{15}{x_{i,j}}=\sum\limits_{j=1}^{15}{[x_{i-b_i,j}+x_{i-b_i,j}a_i(1-c_i)]} \end{cases} ⎩⎪⎪⎨⎪⎪⎧money_ini=money_outi−1+j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]money_ini=money_outi+p+j=1∑15xi,j
然后基于我们对于题目的分析与各类情况的思考,可以得到以下几点:
- 当剩余天数少于该债券周期的话,那么必然不买这个债券。
- 因为债券最小周期为2天,且采用贪心策略,所以前两天必定是全部花费。(在第三问及第四问中,应留下用于每天捐赠的钱)
- 因为是贪心策略,所以 m o n e y _ o u t i money\_out_i money_outi只有在最后一天不为0(该特性为第二问独有,第三问与第四问需考虑给捐款存钱的情况)
将其转化为符号语言即为:
{ ∑ j = 1 15 ∑ i = 31 − b j 30 x i , j = 0 ∑ j = 1 15 x 1 , j + x 2 , j = 2 p \begin{cases} \sum\limits_{j=1}^{15}{\sum\limits_{i=31-b_j}^{30}{x_{i,j}}}=0\\ \sum\limits_{j=1}^{15}{x_{1,j}+x_{2,j}}=2p \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧j=1∑15i=31−bj∑30xi,j=0j=1∑15x1,j+x2,j=2p
2.4、明确约束
首先根据常识,可以得到如下几条约束:
{ x i , j > = 0 p > = 0 m o n e y _ i n i > = m o n e y _ o u t i > = 0 \begin{cases} x_{i,j}>=0\\ p>=0\\ money\_in_i>=money\_out_i>=0 \end{cases} ⎩⎪⎨⎪⎧xi,j>=0p>=0money_ini>=money_outi>=0
然后根据那四条投资要求,可得出以下四个约束:
{ ∑ j = 1 15 ( b j ∑ i = 1 30 x i , j ) ≤ 10 ∑ j = 1 15 ∑ i = 1 30 x i , j ∑ j = 1 15 ( d j ∑ i = 1 30 x i , j ) ≥ 2.5 ∑ j = 1 15 ∑ i = 1 30 x i , j ∑ i = 1 30 ( x i , 1 + x i , 2 + x i , 3 ) > 0.2 ∑ j = 1 15 ∑ i = 1 30 x i , j ∑ i = 1 30 ( x i , 3 k + x i , 3 k − 1 + x k , 3 j − 2 ) > 0.1 ∑ j = 1 15 ∑ i = 1 30 x i , j , ( k ∈ { 2 , 3 , 4 , 5 } ) \begin{cases} \sum\limits_{j=1}^{15}{(b_j\sum\limits_{i=1}^{30}{x_{i,j}})}≤10\sum\limits_{j=1}^{15}{\sum\limits_{i=1}^{30}{x_{i,j}}}\\ \sum\limits_{j=1}^{15}{(d_j\sum\limits_{i=1}^{30}{x_{i,j}})}≥2.5\sum\limits_{j=1}^{15}{\sum\limits_{i=1}^{30}{x_{i,j}}}\\ \sum\limits_{i=1}^{30}(x_{i,1}+x_{i,2}+x_{i,3})>0.2\sum\limits_{j=1}^{15}{\sum\limits_{i=1}^{30}{x_{i,j}}}\\ \sum\limits_{i=1}^{30}(x_{i,3k}+x_{i,3k-1}+x_{k,3j-2})>0.1\sum\limits_{j=1}^{15}{\sum\limits_{i=1}^{30}{x_{i,j}}},(k\in\{2,3,4,5\}) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧j=1∑15(bji=1∑30xi,j)≤10j=1∑15i=1∑30xi,jj=1∑15(dji=1∑30xi,j)≥2.5j=1∑15i=1∑30xi,ji=1∑30(xi,1+xi,2+xi,3)>0.2j=1∑15i=1∑30xi,ji=1∑30(xi,3k+xi,3k−1+xk,3j−2)>0.1j=1∑15i=1∑30xi,j,(k∈{ 2,3,4,5})
暂时想到这些。