算法之分治法解决平面最近点对问题

问题描述：
给定平面上n个点，找其中的一对点，使得在n个点的所有点对中，该点对的距离最小。严格地说，最接近点对可能多于1对。为了简单起见，这里只限于找其中的一对。

思路：
设S中的点为平面上的点，它们都有2个坐标值x和y。为了将平面上点集S线性分割为大小大致相等的2个子集S1和S2，我们选取一垂直线l:x=m来作为分割直线。其中m为S中各点x坐标的中位数。由此将S分割为S1={p∈S|px≤m}和S2={p∈S|px>m}。从而使S1和S2分别位于直线l的左侧和右侧，且S=S1∪S2 。
由于m是S中各点x坐标值的中位数，因此S1和S2中的点数大致相等。递归地在S1和S2上解最接近点对问题，我们分别得到S1和S2中的最小距离d1和d2。现设d=min(d1,d2)。若S的最接近点对(p,q)之间的距离d(p,q)
P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有n2/4对这样的候选者。但是P1和P2中的点具有以下的稀疏性质，它使我们不必检查所有这n^2/4对候选者。考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者，则必有d(p,q)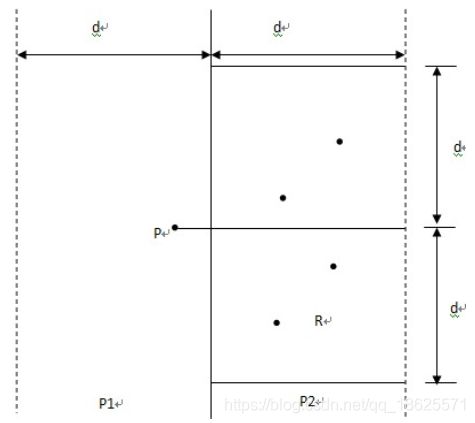
因此，若将P1和P2中所有S的点按其y坐标排好序，则对P1中所有点p，对排好序的点列作一次扫描，就可以找出所有最接近点对的候选者，对P1中每一点最多只要检查P2中排好序的相继6个点。

//用类PointX和PointY表示依x坐标和y坐标排好序的点
class PointX {
	public:
		int operator<=(PointX a)const
		{ return (x<=a.x); }
		int ID; //点编号
		float x,y; //点坐标
};

class PointY {
	public:
		int operator<=(PointY a)const
		{ return(y<=a.y); }
		int p; //同一点在数组x中的坐标
		float x,y; //点坐标
};
#include 
#include
#include
#include
#include
#include
#include

using namespace std;
const int M=50;
float Random();
template 
float dis(const Type&u,const Type&v);
bool Cpair2(PointX X[], int n,PointX& a,PointX& b, float& d);
void closest(PointX X[],PointY Y[],PointY Z[], int l, int r,PointX& a,PointX& b,float& d);
template 
void Copy(Type a[],Type b[], int left,int right);
template 
void Merge(Type c[],Type d[],int l,int m,int r);
template 
void MergeSort(Type a[],Type b[],int left,int right);
int main()
{
	srand((unsigned)time(0));
	int length;
	cout<<"请输入点对数：";
	cin>>length;

	PointX X[M];
	cout<<"随机生成的二维点对为："<
inline float dis(const Type& u,const Type& v)
{
	float dx=u.x-v.x;
	float dy=u.y-v.y;
	return sqrt(dx*dx+dy*dy);
}

bool Cpair2(PointX X[], int n,PointX& a,PointX& b,float& d)
{
	if(n<2) return false;
	PointX* tmpX = new PointX[n];
	MergeSort(X,tmpX,0,n-1);

	PointY* Y=new PointY[n];
	for(int i=0;im) Z[g++]=Y[i];
		else Z[f++]=Y[i];
	}

	closest(X,Z,Y,l,m,a,b,d);
	float dr;
	PointX ar,br;
	closest(X,Z,Y,m+1,r,ar,br,dr);

	if(dr
void Merge(Type c[],Type d[],int l,int m,int r)
{
	int i = l,j = m + 1,k = l;
	while((i<=m)&&(j<=r))
	{
		if(c[i]<=c[j])
		{
			d[k++] = c[i++];
		}
		else
		{
			d[k++] = c[j++];
		}
	}

	if(i>m)
	{
		for(int q=j; q<=r; q++)
		{
			d[k++] = c[q];
		}
	}
	else
	{
		for(int q=i; q<=m; q++)
		{
			d[k++] = c[q];
		}
	}
}

template 
void MergeSort(Type a[],Type b[],int left,int right)
{
	if(left
void Copy(Type a[],Type b[], int left,int right)
{
	for(int i=left;i<=right;i++)
		a[i]=b[i];
}