Paddle安装问题以及实现简单的房价预测——飞桨学习笔记

一、paddle安装问题

1.安装

paddle飞桨安装步骤，安装问题，安装说明，使用教程，戳链接：https://www.paddlepaddle.org.cn/install/quick

快速安装方法：
PaddlePaddle支持使用pip快速安装， 执行下面的命令完成CPU版本的快速安装：

pip install -U paddlepaddle

如需安装GPU版本的PaddlePaddle，执行下面的命令完成GPU版本的快速安装:

pip install -U paddlepaddle-gpu

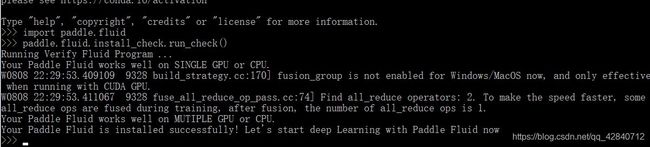
2.验证
在命令框里输入：

import paddle.fluid
paddle.fluid.install_check.run_check()

如果出现下图，则成功安装。

二、房价预测

使用飞桨构建波士顿房价预测模型：

1. 数据处理

#加载相关类库
import paddle
import paddle.fluid as fluid          # 飞桨的主库，目前大部分的实用函数均在paddle.fluid包内
import paddle.fluid.dygraph as dygraph    # 动态图的类库
from paddle.fluid.dygraph import Linear   # 神经网络的全连接层函数，即包含所有输入权重相加和激活函数的基本神经元结构.
import numpy as np
import os
import random

def load_data():
    # 从文件导入数据
    datafile = './work/housing.data'
    data = np.fromfile(datafile, sep=' ')

    # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
                      'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)

    # 将原始数据进行Reshape，变成[N, 14]这样的形状
    data = data.reshape([data.shape[0] // feature_num, feature_num])

    # 将原数据集拆分成训练集和测试集
    # 这里使用80%的数据做训练，20%的数据做测试
    # 测试集和训练集必须是没有交集的
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]

    # 计算train数据集的最大值，最小值，平均值
    maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
                                 training_data.sum(axis=0) / training_data.shape[0]
    
    # 记录数据的归一化参数，在预测时对数据做归一化
    global max_values
    global min_values
    global avg_values
    max_values = maximums
    min_values = minimums
    avg_values = avgs

    # 对数据进行归一化处理
    for i in range(feature_num):
        #print(maximums[i], minimums[i], avgs[i])
        data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])

    # 训练集和测试集的划分比例
    #ratio = 0.8
    #offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    test_data = data[offset:]
    return training_data, test_data

2. 模型设计
   实现过程分如下两步：

定义init函数：在类的初始化函数中声明每一层网络的实现函数。
定义forward函数：构建神经网络结构，实现前向计算过程，并返回预测结果，在本任务中返回的是房价预测结果。

class Regressor(fluid.dygraph.Layer):
    def __init__(self):
        super(Regressor, self).__init__()
        
        # 定义一层全连接层，输出维度是1，激活函数为None，即不使用激活函数
        self.fc = Linear(input_dim=13, output_dim=1, act=None)
    
    # 网络的前向计算函数
    def forward(self, inputs):
        x = self.fc(inputs)
        return x

3. 训练配准
   ① 以guard函数指定运行训练的机器资源，表明在with作用域下的程序均执行在本机的CPU资源上。
   ②声明定义好的回归模型Regressor实例，并将模型的状态设置为训练。
   ③使用load_data函数加载训练数据和测试数据。
   ④设置优化算法和学习率，优化算法采用随机梯度下降SGD，学习率设置为0.01

# 定义飞桨动态图的工作环境
with fluid.dygraph.guard():
    # 声明定义好的线性回归模型
    model = Regressor()
    # 开启模型训练模式
    model.train()
    # 加载数据
    training_data, test_data = load_data()
    # 定义优化算法，这里使用随机梯度下降-SGD
    # 学习率设置为0.01
    opt = fluid.optimizer.SGD(learning_rate=0.01, parameter_list=model.parameters())

4. 训练过程
   数据准备：将一个批次的数据转变成np.array和内置格式。
   前向计算：将一个批次的样本数据灌入网络中，计算输出结果。
   计算损失函数：以前向计算结果和真实房价作为输入，通过损失函数square_error_cost计算出损失函数值（Loss）。
   反向传播：执行梯度反向传播backward函数，即从后到前逐层计算每一层的梯度，并根据设置的优化算法更新参数opt.minimize。

with dygraph.guard(fluid.CPUPlace()):
    EPOCH_NUM = 10   # 设置外层循环次数
    BATCH_SIZE = 10  # 设置batch大小
    
    # 定义外层循环
    for epoch_id in range(EPOCH_NUM):
        # 在每轮迭代开始之前，将训练数据的顺序随机的打乱
        np.random.shuffle(training_data)
        # 将训练数据进行拆分，每个batch包含10条数据
        mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
        # 定义内层循环
        for iter_id, mini_batch in enumerate(mini_batches):
            x = np.array(mini_batch[:, :-1]).astype('float32') # 获得当前批次训练数据
            y = np.array(mini_batch[:, -1:]).astype('float32') # 获得当前批次训练标签（真实房价）
            # 将numpy数据转为飞桨动态图variable形式
            house_features = dygraph.to_variable(x)
            prices = dygraph.to_variable(y)
            
            # 前向计算
            predicts = model(house_features)
            
            # 计算损失
            loss = fluid.layers.square_error_cost(predicts, label=prices)
            avg_loss = fluid.layers.mean(loss)
            if iter_id%20==0:
                print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
            
            # 反向传播
            avg_loss.backward()
            # 最小化loss,更新参数
            opt.minimize(avg_loss)
            # 清除梯度
            model.clear_gradients()
    # 保存模型
    fluid.save_dygraph(model.state_dict(), 'LR_model')

5.保存并测试模型

with fluid.dygraph.guard():
    # 保存模型参数，文件名为LR_model
    fluid.save_dygraph(model.state_dict(), 'LR_model')
    print("模型保存成功，模型参数保存在LR_model中")

def load_one_example(data_dir):
    f = open(data_dir, 'r')
    datas = f.readlines()
    # 选择倒数第10条数据用于测试
    tmp = datas[-10]
    tmp = tmp.strip().split()
    one_data = [float(v) for v in tmp]

    # 对数据进行归一化处理
    for i in range(len(one_data)-1):
        one_data[i] = (one_data[i] - avg_values[i]) / (max_values[i] - min_values[i])

    data = np.reshape(np.array(one_data[:-1]), [1, -1]).astype(np.float32)
    label = one_data[-1]
    return data, label

with dygraph.guard():
    # 参数为保存模型参数的文件地址
    model_dict, _ = fluid.load_dygraph('LR_model')
    model.load_dict(model_dict)
    model.eval()

    # 参数为数据集的文件地址
    test_data, label = load_one_example('./work/housing.data')
    # 将数据转为动态图的variable格式
    test_data = dygraph.to_variable(test_data)
    results = model(test_data)

    # 对结果做反归一化处理
    results = results * (max_values[-1] - min_values[-1]) + avg_values[-1]
    print("Inference result is {}, the corresponding label is {}".format(results.numpy(), label))