unity 点乘与差乘
一、向量
1、向量的数学定义
向量就是一个数字列表,对于程序员来说一个向量就是一个数组。
向量的维度就是向量包含的“数”的数目,向量可以有任意正数维,标量可以被认为是一维向量。
书写向量时,用方括号将一列数括起来,如[1,2,3] 水平书写的向量叫行向量 垂直书写的向量叫做列向量
2、向量的几何意义
几何意义上说,向量是有大小和方向的有向线段。向量的大小就是向量的长度(模)向量有非负的长度。
向量的方向描述了空间中向量的指向。
向量的形式:向量定义的两大要素——大小和方向,有时候需要引用向量的头和尾,下图所示,箭头是向量的末端,箭尾是向量的开始
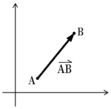
向量中的数表达了向量在每个维度上的有向位移,例如2D向量列出的是沿x坐标方向和y坐标方向的位移。
3 unity中的向量 Vector类
Vector2 二维向量,表示 2D 的向量和点
Vector3 三维向量,表示3D的向量和点
Vector3.normalized 规范化,返回向量的长度为1(只读)。
Vector3.magnitude 长度,返回向量的长度(只读)。
Vector3.Angle 角度 , Angle (from : Vector3, to : Vector3) ,由from和to两者返回一个角度。形象的说,from和to的连线和它们一个指定轴向的夹角
二、点乘
1 点乘的数学意义
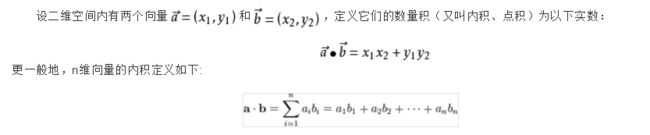
2 点乘的几何意义

3点乘的特点
在向量u,向量v非零的前提下,点积如果为负,则u,v形成的角大于90度;
如果为零,那么u,v垂直;
如果为正,那么u,v形成的角小于90度。
3 点乘在unity中的应用
Vector3.Dot 点乘,对于normalized向量,如果他们指向在完全相同的方向,Dot返回1。如果他们指向完全相反的方向,返回-1。对于其他的情况返回一个数(例如:如果是垂直的Dot返回0)。对于任意长度的向量,Dot返回值是相同的:当向量之间的角度减小,它们得到更大的值。
三、叉乘
1 叉乘的数学意义
表示方法
两个向量a和b的叉积写作a×b(有时也被写成a∧b,避免和字母x混淆)。
定义
向量积可以被定义为:
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0° ≤ θ ≤ 180°),它位于这两个矢量所定义的平面上。)
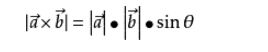
方向:a向量与b向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。(一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。)
也可以这样定义(等效):
向量积|c|=|a×b|=|a| |b|sin
四、点乘与叉乘在项目中的应用
项目需求:
1 通过点乘计算物体B在物体A的前方还是后方
2 通过叉乘,计算物体A转向物体B时,最小角的旋转方向
实现过程:
首先计算出物体A的前方朝向向量v_Bz=B.transform.forward,然后计算物体B相对于物体A的位置向量 v_AB = A.position - B.position;
通过计算v_Bz与v_AB向量点乘结果的正负,判断物体B在物体A的前后
如果物体B在物体A前方, Vector3.Dot(v_Bz,v_AB)大于0
如果物体B在物体A后方, Vector3.Dot(v_Bz,v_AB)小于0
通过计算v_Bz与v_AB向量叉乘的结果,判断旋转方向
如果逆时针旋转,v_C = Vector3.Cross(v_Bz, v_AB)为沿y轴负方向
如果顺时针旋转,v_C = Vector3.Cross(v_Bz, v_AB)为沿y轴正方向
using UnityEngine;
using System.Collections;
public class Vector3_Dot : MonoBehaviour {
public Transform A, B;
Vector3 v_Bz, v_AB, v_A,v_B,v_C;
string str = "";
// Use this for initialization
void Start()
{
}
// Update is called once per frame
void Update()
{
//点乘
v_Bz = B.transform.forward;//B.transform.TransformDirection(Vector3.forward);
v_AB = A.position - B.position;
float f = Vector3.Dot(v_Bz,v_AB);
if (f>0)
{
str = "A在B自身座标系的前方";
}
else if (f<0)
{
str = "A在B自身座标系的后方";
}
else
{
str = "A在B自身座标系的左前方或右方";
}
//差乘
v_A = A.position;
v_B = B.position;
v_C = Vector3.Cross(v_Bz, v_AB);
// A.Rotate(0,0,0);
}
void OnGUI()
{
GUI.Label(new Rect(10,10,200,60),str);
}
void OnDrawGizmos()
{
//差乘绘制相关线
Gizmos.color = Color.blue;
Gizmos.DrawLine(-v_C,Vector3.zero);
//点乘绘制相关线
Gizmos.color = Color.yellow;
Gizmos.DrawLine(Vector3.zero,A.position);
Gizmos.color = Color.yellow;
Gizmos.DrawLine(Vector3.zero,B.position);
Gizmos.color = Color.red;
Gizmos.DrawLine(A.position, B.position);
Gizmos.color = Color.red;
Gizmos.DrawLine(Vector3.zero,v_AB);
Gizmos.color = Color.green;
// Gizmos.DrawLine(A.transform.position, Vector3.left);
}
}
![]()
总结:
点乘可以判断向量之间的夹角,叉乘可以判断向量之间的方向在顺时针还是逆时针方向