AABB包围盒与光线相交的检测算法

1. 表示方法

给出三种表示AABB的方法：

（1） Max-min表示法：使用一个右上角和左下角的点来唯一的定义一个包围体；

（2）Center-radious表示法：我们用center点来表示中点，radious是一个数组，保存了包围盒在x方向，y方向，z方向上的半径。

（3）Min-Width表示方法：我们用min来定义左下角的点，使用width来保存在x，y，z方向上的长度。

    不同的方法，他们的碰撞检测算法也会有所不同，并且不同的表示方法也会适用在不同的情形下。

 

2. Ray-AABB交叉检测算法（Slabs method） 

• 算法理解

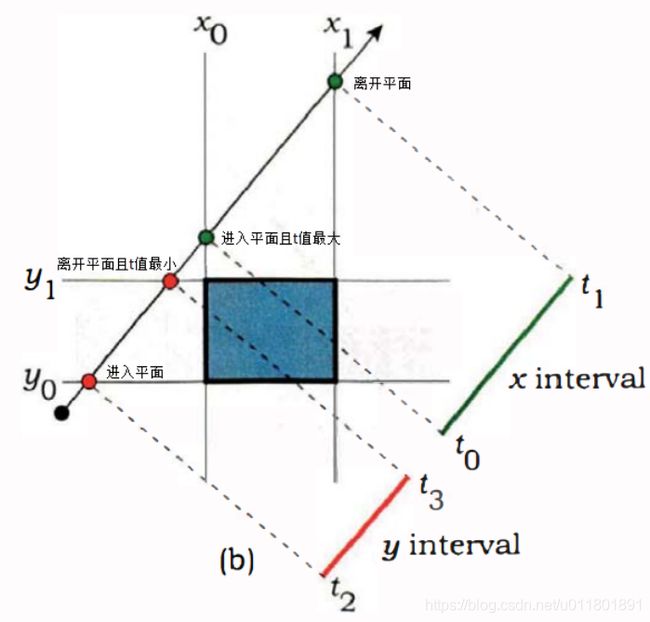
下面是射线与平面不相交的情况：

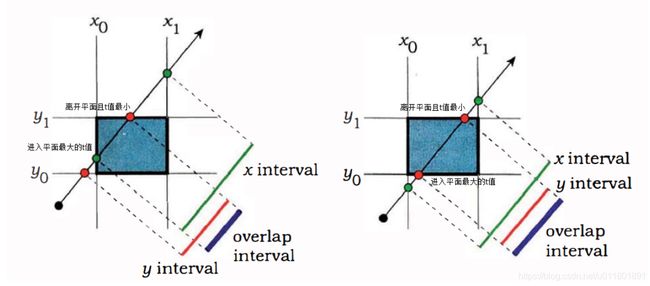
下面是射线与平面相交的情况：

观察上述三幅图可以得出，只要发生区间交叠，光线与平面就能相交，区间交叠出现的条件是：光线进入平面处的最大t值（例如左图靠左的绿点）小于光线离开平面处的最小t值（例如左图靠右的红点）

 

问题转化：

问题就变成了如何求光线进入平面处的最大t值，和光线离开平面处的最小t值

这个问题通过光线与平面相交的参数方程求解就可以了，

光线的参数方程为R(t) = O + t * Dir，变换形式后得到：

t = (R(t) - O.x) / Dir.x

如果光线R(t)与平面相交，则交点R(tins)也应满足平面方程。

一般平面方程为aX+bY+cZ+d=0，因为AABB的六个面分别平行于XY、XZ、YZ平面，所以平面的方程为X=d，Y=d，Z=d。这样的话，就可以用d来代换平面上的交点R(tins),得到下列表达式：

 

光线与垂直于x轴的两个面相交时，t = (d - O.x) / Dir.x

光线与垂直于y轴的两个面相交时，t = (d - O.y) / Dir.y

光线与垂直于z轴的两个面相交时，t = (d - O.z) / Dir.z

 

求得t之后，根据上文的交叠条件，就能判断出射线与平面是否相交。注意到t<0时，交点位于光线的起点之后，则光线（射线）并未与盒体发生相交。

 

• 举例：用Max-min表示法的AABB与射线求交举例

用Max-min表示法来代表AABB时，这个d可以设为左下角点对应的三个面（d=AaBbMin.x,d= AaBbMin.y,d= AaBbMin.z），和右上角点对应的三个面（d=AaBbMax.x,d= AaBbMax.y,d= AaBbMax.z）

（1）求t：

找到两组平面对应的两组t，可对照下面代码查看。BottomT对应左下角点的三个面的t，TopT对应右上角点三个面的t。

（2）找到最小最大t

找到所有t中最小的MinT（分别找到x，y，z方向上各自最小的t）和最大的MaxT。

目的：这里主要是要找到近面上所有可能的t（MinT），和远面上所有可能的t（MaxT）

（3）找到最可能使条件满足的一对近面t和远面t

找到近面t（MinT）中的最大（LargestMinT）和远面t（MaxT）中的最小（LargestMaxT）

（4）判断是否相交

用刚才找出的可能性最大的一队来比较，比较标准是：

远面t>近面t，则交点存在。

 

再来回看下最初的交叠条件：

光线进入平面处的最大t值，小于光线离开平面处的最小t值。

光线进入的平面就是第(4)步里的近面，最大t值，就是LargestMinT，所以判断条件就是LargestMaxT > LargestMinT，则产生交点。

 

下面给出代码，该代码片段摘自ExposureRender

DEV bool IntersectBox(const CRay& R, float* pNearT, float* pFarT)
{
	const Vec3f InvR		= Vec3f(1.0f, 1.0f, 1.0f) / R.m_D;
	const Vec3f BottomT		= InvR * (Vec3f(gAaBbMin.x, gAaBbMin.y, gAaBbMin.z) - R.m_O);
	const Vec3f TopT		= InvR * (Vec3f(gAaBbMax.x, gAaBbMax.y, gAaBbMax.z) - R.m_O);
	const Vec3f MinT		= MinVec3f(TopT, BottomT);
	const Vec3f MaxT		= MaxVec3f(TopT, BottomT);
	const float LargestMinT = fmaxf(fmaxf(MinT.x, MinT.y), fmaxf(MinT.x, MinT.z));
	const float LargestMaxT = fminf(fminf(MaxT.x, MaxT.y), fminf(MaxT.x, MaxT.z));

	*pNearT = LargestMinT;
	*pFarT	= LargestMaxT;

	return LargestMaxT > LargestMinT;
}

其中用到的几个函数为：

inline HOD Vec3f MinVec3f(Vec3f a, Vec3f b)
{
	return Vec3f(min(a.x, b.x), min(a.y, b.y), min(a.z, b.z));
}

inline HOD Vec3f MaxVec3f(Vec3f a, Vec3f b)
{
	return Vec3f(max(a.x, b.x), max(a.y, b.y), max(a.z, b.z));
}

inline float fminf(float a, float b)
{
    return a < b ? a : b;
}

inline float fmaxf(float a, float b)
{
    return a > b ? a : b;
}

参考：

https://blog.csdn.net/linuxheik/article/details/53395394