《数据结构与算法之美》16～20笔记

关于我的仓库

• 这篇文章是我为面试准备的学习总结中的一篇
• 我将准备面试中找到的所有学习资料，写的Demo，写的博客都放在了这个仓库里iOS-Engineer-Interview
• 欢迎star??
• 其中的博客在简书，CSDN都有发布
• 博客中提到的相关的代码Demo可以在仓库里相应的文件夹里找到

前言

• 该系列为学习《数据结构与算法之美》的系列学习笔记
• 总结规律为一周一更，内容包括其中的重要知识带你，以及课后题的解答
• 算法的学习学与刷题并进，希望能真正养成解算法题的思维
• LeetCode刷题仓库：LeetCode-All-In
• 多说无益，你应该开始打代码了

16讲二分查找（下）：如何快速定位IP对应的省份地址

• 十个二分九个错，确实感触很深，一个字，学

• 唐纳德·克努特（Donald E.Knuth）在《计算机程序设计艺术》的第3卷《排序和查找》中说到：“尽管第一个二分查找算法于1946年出现，然而第一个完全正确的二分查找算法实现直到1962年才出现。”

变体一：查找第一个值等于给定值的元素

• hard做法【简洁】

// 变体一：查找第一个值等于给定值的元素[hard]
int BinarySearchXH(vector &arr, int value) {
	
	int len = arr.size();
	int left = 0;
	int right = len - 1;
	int mid = left + ((right - left) >> 1);
	while (left <= right) {
		mid = left + ((right - left) >> 1);
		if (arr[mid] >= value) {
			right = mid - 1;
		} else {
			left = mid + 1;
		} 
	}
	
	if (left < len && arr[left] == value) {
		return left;
	} else {
		return -1;
	}
}
// 其实这种做法也没有那么难理解，只是对arr[mid] = value的情况将它视作没找到，继续进行二分
// 就和上一章总结的那样，如果出现的是return right会返回最接近那个，这里使用的是return left返回的就是第一个了

• easy做法：

// 变体一：查找第一个值等于给定值的元素[easy]
int BinarySearchXE(vector &arr, int value) {
	
	int len = arr.size();
	int left = 0;
	int right = len - 1;
	int mid = left + ((right - left) >> 1);
	while (left <= right) {
		mid = left + ((right - left) >> 1);
		if (arr[mid] > value) {
			right = mid - 1;
		} else if (arr[mid] < value) {
			left = mid + 1;
		} else {
			if ((mid == 0) || (arr[mid - 1] != value)) {
				return mid;
			} else {
				right = mid - 1;
			}
		}
	}
	
	return -1;
}

// 没啥好说的，很简单就是对与找到的mid不一定是第一个，遥往前找
// 这里其实找到一个一直往前推也可以，当然这样慢了，没有二分的优越性了

变体二：查找最后一个值等于给定值的元素

• 这题目好划。。。

// 变体二：查找最后一个值等于给定值的元素
int BinarySearchY(vector &arr, int value) {
	
	int len = arr.size();
	int left = 0;
	int right = len - 1;
	int mid = left + ((right - left) >> 1);
	while (left <= right) {
		mid = left + ((right - left) >> 1);
		if (arr[mid] > value) {
			right = mid - 1;
		} else if (arr[mid] < value) {
			left = mid + 1;
		} else {
			if ((mid == len - 1) || (arr[mid + 1] != value)) {
				return mid;
			} else {
				left = mid + 1;
			}
		}
	}
	
	return -1;
}

变体三：查找第一个大于等于给定值的元素

• 感觉老师确实有一手
• 对于这类题目，我以前可以会在原二分基础上修修改改碰碰运气，但是老师给了个其实还是可以按照二分的思路一点点的看

// 变体三：查找第一个大于等于给定值的元素
int BinarySearchZ(vector &arr, int value) {
	
	int len = arr.size();
	int left = 0;
	int right = len - 1;
	int mid = left + ((right - left) >> 1);
	while (left <= right) {
		mid = left + ((right - left) >> 1);
		if (arr[mid] >= value) {
			if ((mid == 0) || (arr[mid - 1] < value)) {
				return mid;
			} else {
				right = mid - 1;
			}
		} else {
			left = mid + 1;
		}
	}	
	return -1;
}

变体四：查找最后一个小于等于给定值的元素

• 划水呀 划水呀

// 变体四：查找最后一个小于等于给定值的元素
int BinarySearchZA(vector &arr, int value) {
	
	int len = arr.size();
	int left = 0;
	int right = len - 1;
	int mid = left + ((right - left) >> 1);
	while (left <= right) {
		mid = left + ((right - left) >> 1);
		if (arr[mid] > value) {
			right = mid - 1;
		} else {
			if ((mid == len - 1) || (arr[mid + 1] > value)) {
				return mid;
			} else {
				left = mid + 1;
			}
		}
	}
	
	return -1;
}

开篇题目：如何快速定位出一个IP地址的归属地？

• 当我们想要查询202.102.133.13这个IP地址的归属地时，我们就在地址库中搜索，发现这个IP地址落在[202.102.133.0, 202.102.133.255]这个地址范围内，那我们就可以将这个IP地址范围对应的归属地“山东东营市”显示给用户了。

[202.102.133.0, 202.102.133.255]  山东东营市 
[202.102.135.0, 202.102.136.255]  山东烟台 
[202.102.156.34, 202.102.157.255] 山东青岛 
[202.102.48.0, 202.102.48.255] 江苏宿迁 
[202.102.49.15, 202.102.51.251] 江苏泰州 
[202.102.56.0, 202.102.56.255] 江苏连云港

• 当我们要查询某个IP归属地时，我们可以先通过二分查找，找到最后一个起始IP小于等于这个IP的IP区间，然后，检查这个IP是否在这个IP区间内，如果在，我们就取出对应的归属地显示；如果不在，就返回未查找到。

课后题：LeetCode 33 搜索旋转有序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

class Solution {
public:
    int search(vector& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] < nums[right]) {
                if (nums[mid] < target && nums[right] >= target) left = mid + 1;
                else right = mid - 1;
            } else {
                if (nums[left] <= target && nums[mid] > target) right = mid - 1;
                else left = mid + 1;
            }
        }
        return -1;
    }
};

• 其实也很简单，就是找有序的那段进行判断，不在里面就分另一段

17讲跳表：为什么Redis一定要用跳表来实现有序集合

• 这个很新鲜啊，跳表，不说了哦，学
• 但是它确实是一种各方面性能都比较优秀的动态数据结构，可以支持快速的插入、删除、查找操作，写起来也不复杂，甚至可以替代（Red-black tree）

理解跳表

• 先看原始单链表数据

• 下一步我们是每两个节点中提取一个座位索引放在索引层

• 现在假如我们要查找一个16，在索引层发现在13 17之间，我们就会从13下降到原始链表层，在原始链表层继续查找，就找到16了

• 当然一层看到不够，我们会继续往上建，直到索引层只剩2，3个索引值

• 现在，我们来看下假如查找一个64个节点的链表的，我们只需要经过几个节点呢？

• 好快！

跳表的优越性

• 第k级索引的结点个数是第k-1级索引的结点个数的1/2，那第k级索引结点的个数就是n/(2k)。
• 在每一级，注意是每一级，都最多只要经过三个节点就能遍历完

• 此时我们实现了查找任意数据的时间复杂度为O(logn)，在单链表中实现了二分查找，空间换时间计划通✅
• 空间复杂度O(n)

跳表的操作

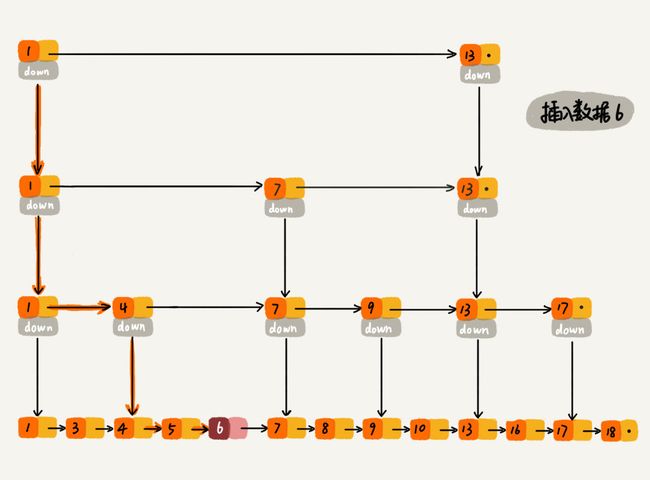
• 我们看一个插入数据的操作，插入一个数据6

• 这里会出现一个问题，我们在两集索引之间插入过多节点会导致其搜索效率降低，这就还涉及到了跳表索引的动态更新
• 跳表通过随机函数的方式进行动态更新，比如每次能生成一个随机数k，在插入数据后，就在第1到k层索引层中插入该数据

• 不要问，问就是已经懂了

解答开篇：为什么Redis中的有序集合是通过跳表来实现的

• 其中，插入、删除、查找以及迭代输出有序序列这几个操作，红黑树也可以完成，时间复杂度跟跳表是一样的。但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。
• 对于按照区间查找数据这个操作，跳表可以做到O(logn)的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了。这样做非常高效。

课后题：在今天的内容中，对于跳表的时间复杂度分析，我分析了每两个结点提取一个结点作为索引的时间复杂度。如果每三个或者五个结点提取一个结点作为上级索引，对应的在跳表中查询数据的时间复杂度是多少呢？

• 如果每三个或者五个节点提取一个节点作为上级索引，那么对应的查询数据时间复杂度，应该也还是 O(logn)。
• 假设每 5 个节点提取，那么最高一层有 5 个节点，而跳表高度为 log5n，每层最多需要查找 5 个节点，即 O(mlogn) 中的 m = 5，最终，时间复杂度为 O(logn)。
• 空间复杂度也还是 O(logn)，虽然省去了一部分索引节点，但是似乎意义不大。

18讲散列表（上）：Word文档中的单词拼写检查功能是如何实现的

• 散列即是哈希
• 散列表用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表。
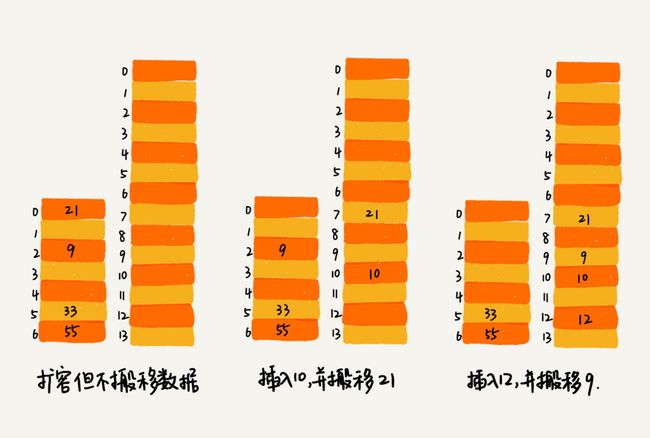
• 假如我们用十个数字0到9要放到长度为10的数组里面，那我们只要把对应数字放在相应下标上即可
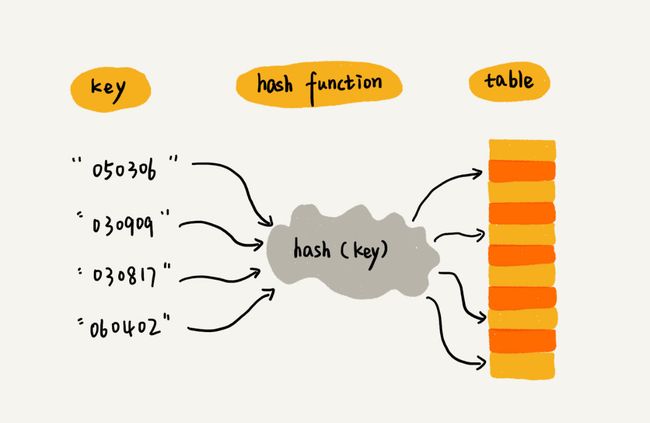
• 但是如果我们同样是存放十个数据，可它的值不是0到9，那就需要我们通过哈希函数去计算散列值

散列函数

• 散列函数计算得到的散列值是一个非负整数

• 如果key1 = key2，那hash(key1) == hash(key2)

• 如果key1 ≠ key2，那hash(key1) ≠ hash(key2)

散列冲突

开放寻址法

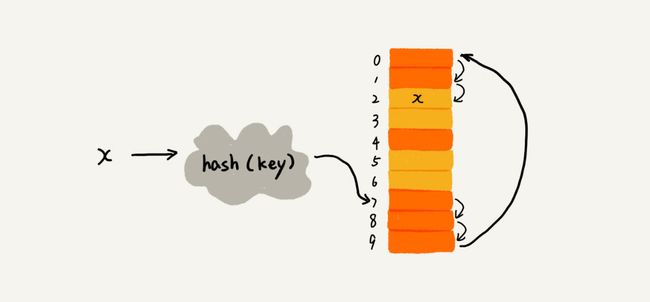
• 线性探测（Linear Probing）通过散列函数求出的散列值如果上面已经有数据了，就继续往下搜索，直到找到空闲位置，进行插入

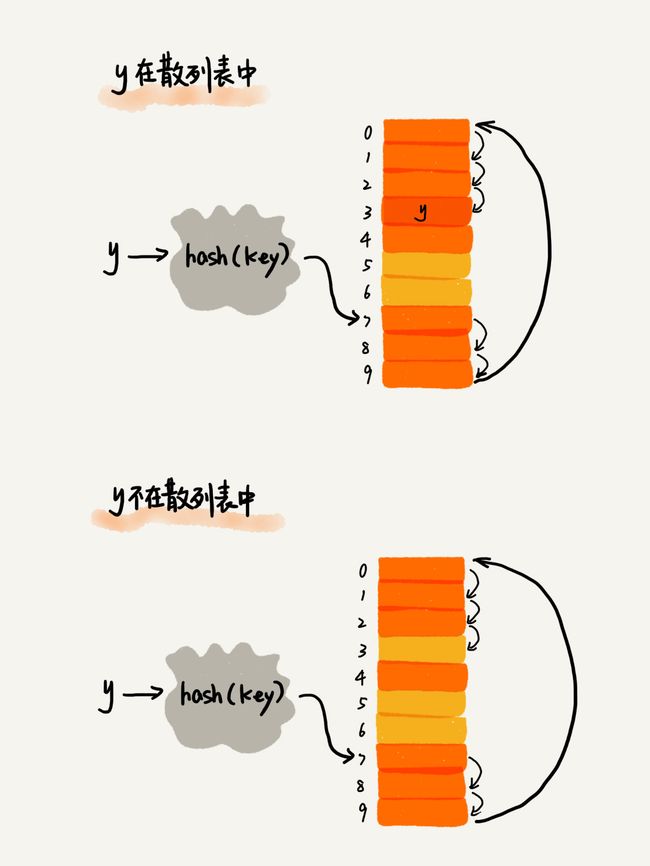
• 查找时比较数组中下标为散列值的元素和要查找的元素，如果一直查找到空闲位置，还是没找到该元素，说明它不在表里。这里我觉得你要分清楚，一般我们哈希表是用来进行记录的，查找是为了判断该元素是否在表里，比如C++ map里面的find()函数，也就是说虽然我们已经有这个数据了，还要去查找看起来很蠢，但这并不矛盾，我们在意的，仅仅是记录本身而已

• 但这样还是有个问题，由于我们会进行线性探测，所以的当我们删除数据的时候，如果我们删除的数据时通过线性探测得出来的，这样就会出现数据本身应该算在空闲位置那一块
• 什么意思呢？就是说如果在删除数据时，我们简单的清空元素会导致后面进行线性探测的时候，在查看到该位置时就认做找不到该元素【因为已经到空闲位置了】，所以我们要对后面删除的位置设置deleted标志位

• 我们可以将删除的元素，特殊标记为deleted。当线性探测查找的时候，遇到标记为deleted的空间，并不是停下来，而是继续往下探测。
• 线性探测法其实存在很大问题。当散列表中插入的数据越来越多时，散列冲突发生的可能性就会越来越大，空闲位置会越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，所以最坏情况下的时间复杂度为O(n)。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据
• 二次探测（Quadratic probing）：线性探测每次探测的步长是1，那它探测的下标序列就是hash(key)+0，hash(key)+1，hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”，也就是说，它探测的下标序列就是hash(key)+0，hash(key)+12，hash(key)+22……
• 双重散列（Double hashing）：仅要使用一个散列函数。我们使用一组散列函数hash1(key)，hash2(key)，hash3(key)……我们先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依次类推，直到找到空闲的存储位置
• 装载因子（load factor）：表示空位的多少，填入表中的元素个数/散列表的长度，装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降

链表法

• 每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。

• 当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是O(1)。当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除
• 这两个操作的时间复杂度跟链表的长度k成正比，也就是O(k)。对于散列比较均匀的散列函数来说，理论上讲，k=n/m，其中n表示散列中数据的个数，m表示散列表中“槽”的个数

解答开篇：Word文档中单词拼写检查功能是如何实现的？

• 当用户输入某个英文单词时，我们拿用户输入的单词去散列表中查找。如果查到，则说明拼写正确；如果没有查到，则说明拼写可能有误，给予提示。借助散列表这种数据结构，我们就可以轻松实现快速判断是否存在拼写错误

课后题

假设我们有10万条URL访问日志，如何按照访问次数给URL排序？

• 遍历 10 万条数据，以 URL 为 key，访问次数为 value，存入散列表，同时记录下访问次数的最大值 K，时间复杂度 O(N)
• 如果 K 不是很大，可以使用桶排序，时间复杂度 O(N)。如果 K 非常大（比如大于 10 万），就使用快速排序，复杂度 O(NlogN)

有两个字符串数组，每个数组大约有10万条字符串，如何快速找出两个数组中相同的字符串？

• 以第一个字符串数组构建散列表，key 为字符串，value 为出现次数。再遍历第二个字符串数组，以字符串为 key 在散列表中查找

19讲散列表（中）：如何打造一个工业级水平的散列表

• 给力哦，全面迈向工业化，多快好省搞起来
• 在极端情况下，有些恶意的攻击者，还有可能通过精心构造的数据，使得所有的数据经过散列函数之后，都散列到同一个槽里。如果我们使用的是基于链表的冲突解决方法，那这个时候，散列表就会退化为链表，查询的时间复杂度就从O(1)急剧退化为O(n)
• 厉害，还有这样的攻击手段
• 这一节就当开开眼吧

散列函数设计

• 散列函数的设计不能太复杂
• 散列函数生成的值要尽可能随机并且均匀分布
• 直接寻址法、平方取中法、折叠法、随机数法等

装载因子过大

• 当装载因子过大，也就是说表里面基本装满的时候，我们就要考虑动态扩容的问题
• 申请一个更大的空间，把老数据搬进来

• 插入一个数据，最好情况下，不需要扩容，最好时间复杂度是O(1)。最坏情况下，散列表装载因子过高，启动扩容，我们需要重新申请内存空间，重新计算哈希位置，并且搬移数据，所以时间复杂度是O(n)。用摊还分析法，均摊情况下，时间复杂度接近最好情况，就是O(1)
• 但在扩容时，不能一次完成，因为将老数据搬入新的表需要耗费大量时间，让用户等待显然不合理，所以我们选择每次执行新的插入时，搬运一次老数据，将操作均摊下去

解决冲突的方法

• 当数据量比较小、装载因子小的时候，适合采用开放寻址法。这也是Java中的ThreadLocalMap使用开放寻址法解决散列冲突的原因
• 链表法最差的时间复杂度也就O(logn)，并且可以结合跳表，二叉树这类数据结构

• 基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表，而且，比起开放寻址法，它更加灵活，支持更多的优化策略，比如用红黑树代替链表

以Java中的HashMap为例看工业级别的散列表实现

• HashMap默认的初始大小是16，当然这个默认值是可以设置的，如果事先知道大概的数据量有多大，可以通过修改默认初始大小，减少动态扩容的次数，这样会大大提高HashMap的性能
• 最大装载因子默认是0.75，当HashMap中元素个数超过0.75*capacity（capacity表示散列表的容量）的时候，就会启动扩容，每次扩容都会扩容为原来的两倍大小
• ashMap底层采用链表法来解决冲突。即使负载因子和散列函数设计得再合理，也免不了会出现拉链过长的情况，一旦出现拉链过长，则会严重影响HashMap的性能。
• 于是，在JDK1.8版本中，为了对HashMap做进一步优化，我们引入了红黑树。而当链表长度太长（默认超过8）时，链表就转换为红黑树。我们可以利用红黑树快速增删改查的特点，提高HashMap的性能。当红黑树结点个数少于8个的时候，又会将红黑树转化为链表。因为在数据量较小的情况下，红黑树要维护平衡，比起链表来，性能上的优势并不明显

20讲散列表（下）：为什么散列表和链表经常会一起使用

LRU缓存淘汰算法

• LRU是在讲链表那一节就提到的算法
  • 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部
  • .如果此数据没有在缓存链表中
    • 如果此时缓存未满，则将此结点直接插入到链表的头部
    • 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部
• 我们使用散列表链表相结合的方式解决这个问题

• 这个问题其实翻译过来就是：我虽然懂散列表是个什么东西，但我就是想要能有序输出里面的东西，这就需要我们在散列表+双向链表之外在加一个拉链【hnext】
• 当我们查找数据的时候，我们是通过散列表，在顺序查找，但当我们是添加数据的时候，需要对链的头尾进行操作，所以要对链进行操作
• 添加操作：我们需要先看这个数据是否已经在缓存中。如果已经在其中，需要将其移动到双向链表的尾部；如果不在其中，还要看缓存有没有满。如果满了，则将双向链表头部的结点删除，然后再将数据放到链表的尾部；如果没有满，就直接将数据放到链表的尾部

Redis有序集合

• 这一块感觉么得意思，鸽了

Java LinkedHashMap

• 这一块和上面的LRU算法一样，同样是通过双向链表+散列来实现的
• 插入的2会出现在链表的末尾

• 此时如果我们要插入新的3数据，会把旧的删除，新的放最后

• 照访问时间排序的LinkedHashMap本身就是一个支持LRU缓存淘汰策略的缓存系统
• LinkedHashMap是通过双向链表和散列表这两种数据结构组合实现的。LinkedHashMap中的“Linked”实际上是指的是双向链表，并非指用链表法解决散列冲突

课后题

今天讲的几个散列表和链表结合使用的例子里，我们用的都是双向链表。如果把双向链表改成单链表，还能否正常工作呢？为什么呢？

• 在删除一个元素时，虽然能 O(1) 的找到目标结点，但是要删除该结点需要拿到前一个结点的指针，遍历到前一个结点复杂度会变为 O(N），所以用双链表实现比较合适。

猎头系统设计

• 根据猎头的ID快速查找、删除、更新这个猎头的积分信息
• 查找积分在某个区间的猎头ID列表
• 查找按照积分从小到大排名在第x位到第y位之间的猎头ID列表
• 解答：
  • ID 在散列表中所以可以 O(1) 查找到这个猎头
  • 积分以跳表存储，跳表支持区间查询
  • 暂时无解