深度之眼Paper带读笔记GNN.03.SDNE
文章目录
- 前言
-
- 论文结构
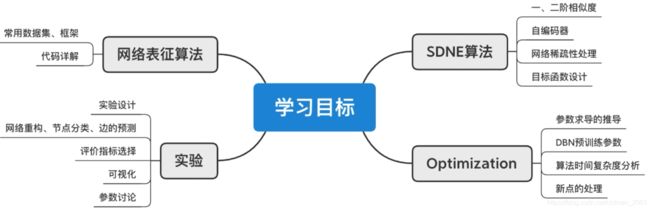
- 学习目标
- 基础知识补充
- 论文研究背景、成果、意义
-
- 研究背景
- 模型框架
- 研究成果
- 摘要核心
- 论文框架
- 算法比较
- 模型详解
-
- 细节一: 一、二阶相似度
- 细节二 :自编码器
- 细节三:网络稀疏性处理
- 细节四:目标函数
- 细节五:优化公式推导
- 细节六:时间复杂度
- 实验设置与分析
- 代码复现
-
- 准备工作
- main
-
- 实现思路
- 具体代码
- model
-
- 损失与代码的对应
- dataset
- draw_cora
- 问题
前言
本课程来自深度之眼,部分截图来自课程视频。
文章标题:Structural Deep Network Embedding
结构化深度网络特征表示
作者:Daixin Wang, Peng Cui, Wenwu Zhu
单位:Tsinghua
发表会议及时间:KDD 2016
公式输入请参考:在线Latex公式
论文结构
- Abstract:提出之前多为浅层模型并提出SDNE模型,使用了一阶相似度和二阶相似度的概念。
- Introduction:介绍学习图的表征的重要性、低维的分布式表达,提出几个难点:非线性、结构保存、稀疏性。与以前的方法ISOMAP、Laplacian eigenmap、LINE等做对比,强调这些是浅层模型无法针对非线性建模,本文提出多层神经网络结构半监督模型(利用一阶相似度)。
- Related Work:深度学习算法在图片、文本上的成功应用;网络表征算法中早期的LLE、ISOMAP,DeepWalk、LINE等浅层模型。
- Model Definition:图的定义以及网络表征学习,一阶相似度和二阶相似度。
- SDNE framework:SDNE的网络结构,损失函数的设计,一阶相似度做有监督、二阶相似度做无监督,如何将自编码器与网络表征算法结合起来。
- Optimization:目标函数对参数求偏导,参数的初始化方法(DBN),时间复杂度分析。
- Dataset and Baselines:选取多类数据集以及DeepWalk、LINE等baselines 。
- Effectiveness:实验探究模型有效性:网络重构、节点分类、边的预测、可视化等,参数设定的讨论。
- Conclusion:总结提出了一种基于自编码器半监督多层神经网路框架。
学习目标
基础知识补充
Macro-F1 vs Micro-F1
Macro-F1:分布计算每个类别的F1,然后做平均
Micro-F1:通过先计算总体的TP,FN和FP的数量,再计算F1
(重点)MAP指标(Mean Average Precision):排序指标
假设我们有一个查询Query 1,通过这个查询得到了5个相关的文档:
■ ■ ■ ■ ■ \blacksquare \blacksquare \blacksquare \blacksquare \blacksquare ■■■■■
但是实际结果一共有10个文档,上面5个文档在这10个文档中的排序(Rank 1)如下:
■ □ ■ □ □ ■ □ □ ■ ■ \blacksquare\square \blacksquare\square \square \blacksquare \square \square \blacksquare \blacksquare ■□■□□■□□■■
那么可以得到:
| ■ \blacksquare ■ | □ \square □ | ■ \blacksquare ■ | □ \square □ | □ \square □ | ■ \blacksquare ■ | □ \square □ | □ \square □ | ■ \blacksquare ■ | ■ \blacksquare ■ | |
|---|---|---|---|---|---|---|---|---|---|---|
| Recall | 0.2 | 0.2 | 0.4 | 0.4 | 0.4 | 0.6 | 0.6 | 0.6 | 0.8 | 1.0 |
| Precision | 1.0 | 0.5 | 0.67 | 0.5 | 0.4 | 0.5 | 0.43 | 0.38 | 0.44 | 0.5 |
Recall的计算是根据命中结果个数算的,Query 1总共命中5个结果,每个结果平均为0.2,Recall显示当前结果共命中多少个结果*结果平均值
Precision 显示:当前结果中命中个数/当前结果个数
然后是Query 2,通过这个查询得到了3个相关的文档:
■ ■ ■ \blacksquare \blacksquare \blacksquare ■■■
但是实际结果一共有10个文档,上面3个文档在这10个文档中的排序(Rank 2)如下:
□ ■ □ □ ■ □ ■ □ □ □ \square \blacksquare\square \square \blacksquare \square\blacksquare \square\square\square □■□□■□■□□□
那么可以得到:
| □ \square □ | ■ \blacksquare ■ | □ \square □ | □ \square □ | ■ \blacksquare ■ | □ \square □ | ■ \blacksquare ■ | □ \square □ | □ \square □ | □ \square □ | |
|---|---|---|---|---|---|---|---|---|---|---|
| Recall | 0.0 | 0.33 | 0.33 | 0.33 | 0.67 | 0.67 | 1.0 | 1.0 | 1.0 | 1.0 |
| Precision | 0.0 | 0.5 | 0.33 | 0.25 | 0.4 | 0.33 | 0.43 | 0.38 | 0.33 | 0.3 |
然后计算加黑部分的平均(Average)精度:
average precision query 1=(1.0+0.67+0.5+0.44+0.5)/5=0.62
average precision query 2=(0.5+0.4+0.43)/3=0.44
然后再算两个Query的精度平均(Mean):
mean average precision=(0.62+0.44)/2=0.53
也就是说这个指标不但比较找到多少个结果,还比较了找到了结果的所在位置,位置越靠前指标得分越高。
论文研究背景、成果、意义
研究背景
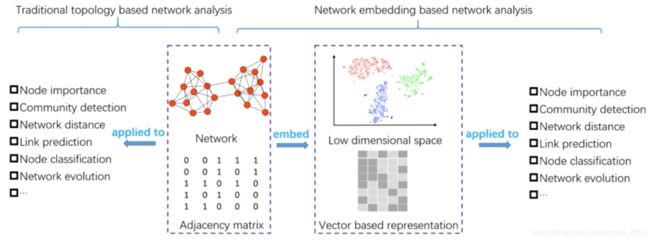
网络表征学习:点的分布式表达、一种降维操作、应用于多个下游任务
Node importance
Community detection
Network distance
Link prediction
Node classification
Network evolution:网络的演化,时序网络,随着时间的推移节点是变化的。
网络学习结构梳理:
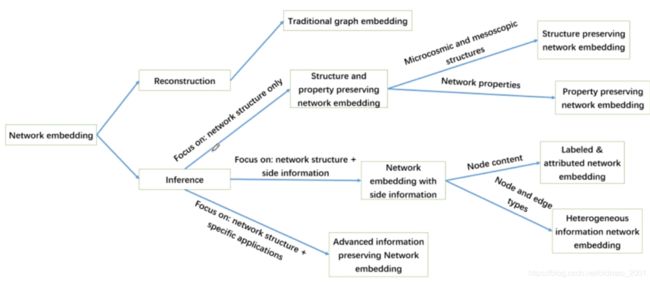
以上每个节点代表的不是一篇论文,而是一类论文。
Reconstruction:学习到的表征要可以还原为原图。
Traditional graph embedding:SVD、LE等不涉及DL的算法,学习能力较差,只适用于还原任务,没有办法做inference。我们这里所学习的基于DL的GNN属于下面那个inference分支。
Property preserving network embedding:通过设计目标函数,让模型偏重于对图结点中属性的表征。
Structure preserving network embedding:图结构的表征。
Labeled & attributed network embedding:作为只考虑图结构信息的一种补充。这里的attributed 和property有什么不一样?attributed 应该是side information,是隐含在结点上的。例如商品,property有价格、大小、重量;attributed 则是有谁买过。
Advanced information preserving Network embedding:这里是指针对某个特定的任务进行表征,不是general的表征去解决多个任务。
模型框架
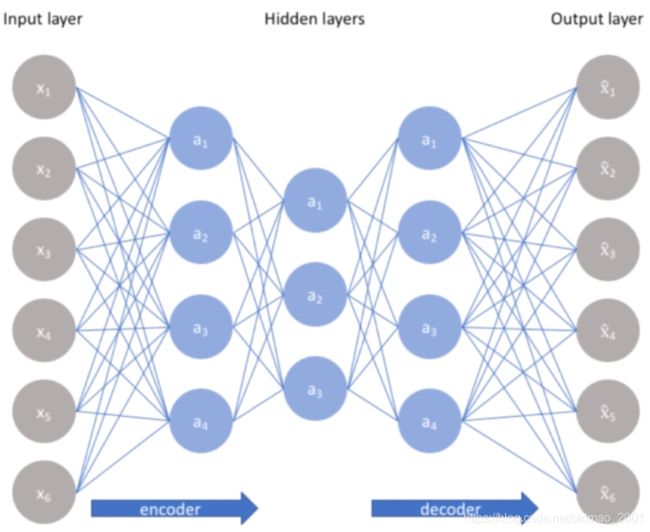
中心思想:AE应用到图学习领域。
下图中 x i x_i xi是(结点 i i i+它的邻居结点)对应的表示,然后对 x i x_i xi进行降维,可以看到 y i ( 1 ) y_i^{(1)} yi(1)要短一点。降维 K K K次之后得到 x i x_i xi对应的embedding: y i ( K ) y_i^{(K)} yi(K),这就是编码部分。
然后是解码,将 y i ( K ) y_i^{(K)} yi(K)还原为 x ^ i \hat x_i x^i
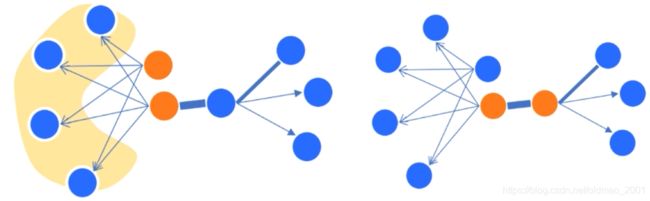
下图有两个点i和j,在解码还原的时候加上了一阶和二阶相似度的约束,例如:如果之前i和j是有边相连的,那么在还原之后的i和j应该也有边相连才行。

一阶相似度:点之间是否有边(右边两个黄色点有边,一阶相似度高)
二阶相似度:邻居之间相似度(左边黄色两个点邻居都一样,二阶相似度高)
二阶相似度维度要高一些
研究成果
自编码器神经网络结构
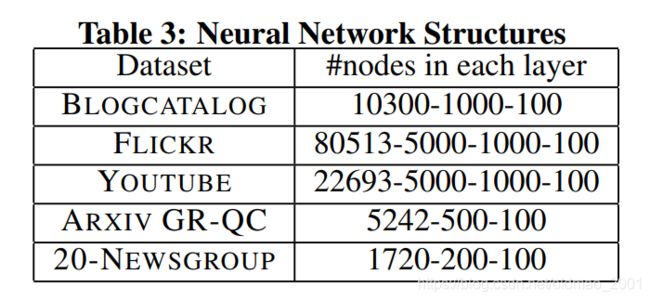
第一行对应BLOGCATALOG数据集,结点数量是10312,因此近似后,输入结点是10300,先降维到1000,然后再降维100。
摘要核心
1.强调之前的模型多为浅层模型,无法模拟复杂的线性空间,从而引出更深的神经网络结构
2.回顾了一阶和二阶相似度在网络中所表达的意义
3.通过一阶和二阶相似度来建模网络中的局部和全局结构
4.将自编码器应用到图学习中,提出一个半监督学习的框架
5.通过多类数据集如语言网络、社交网络和引用网络及多种实验验证了模型的有效性
论文框架
- Introduction
- Related Work
- Structural Deep Network Embedding
3.1Problem Definition
3.2 The Model
3.3 Analysis and Discussions - Experiments
4.1Datasets
4.2 Baseline Algorithms
4.3 Evaluation Metrics
4.4Parameter Settings
4.5 Experiment Results
4.6Parameter Sensitivity - Conclusion
算法比较
1.提出的顺序DeepWalk 2014,LINE2015,Node2Vec 2016(相当于DeepWalk 的改进)=SDNE 2016
2.DeepWalk和Node2Vec是基于随机游走启发的算法,LINE、SDNE是基于网络结构启发的算法
3.SDNE引入了更深层的网络结构,表达能更好,训练开销更大
4.这些算法都是基于图结构不引入额外的信息,适用于一般图,如节点的特征信息、边的类型信息不引入
| Methodology | Advantage | ||
|---|---|---|---|
| Matrix Factorization | Social Dim.[31],[32], GraRep [26], HOPE [35], GraphWave [39],M-NIMF [28], TADW[7], HSCA [20], MMDW[46], DMF[8], LANE[30] | capture global structure | high time and memory cost |
| Random Walk | Deep Walk [6],node2vec [34],APP [36],DDRW[45], GENE [48],TriDNR[50],UPP-SNE [43],struct2vec [38], SNS[40],PPNE[44],SemiNE [49] | relatively efficient | only capture local structure |
| Edge Modeling(一二阶相似度) | LINE [1],TLINE [47],LDE [51],pRBM[29], GraphGAN[37] | efficient(不用产生序列,快) | only capture local structure |
| Deep Learning | DNGR [9],SDNE[19](可以放上面) | capture non-linearity | high time cost |
| Hybrid | DP[41],HARP[42],Planetoid [52] | capture global structure |
模型详解
挑战性:
High non-linearity
Structure preserving
Sparsity
细节一: 一、二阶相似度
一阶相似度:直接邻居
DEFINITION 2. (First-Order Proximity) The first-order proximity describes the pairwise proximity between vertexes. For any pair of vertexes, if s i , j > 0 s_{i,j}>0 si,j>0, there exists positive first-order proximity between v i v_i vi and v j v_j vj. Otherwise, the first-order proximity between v i v_i vi and v j v_j vj is 0.
二阶相似度:邻居间的相似度
DEFINITION 3. (Second-Order Proximity) The second-order proximity between a pair of vertexes describes the proximity of the pair’s neighborhood structure. Let N u = { s u , 1 , … , S u , ∣ V ∣ } N_u =\{ s_{u,1},…, S_{u, |V|}\} Nu={ su,1,…,Su,∣V∣} denote the first-order proximity between v u v_u vu and other vertexes. Then, second-order proximity is determined by the similarity of N u N_u Nu and N v N_v Nv.
例如:
S 5 , 6 = 0 , S 6 , 7 = 1 S_{5,6}=0,S_{6,7}=1 S5,6=0,S6,7=1
N 5 = [ 1 , 1 , 1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 ] N_5=[1,1,1,1,0,0,0,0,0,0] N5=[1,1,1,1,0,0,0,0,0,0]
N 6 = [ 1 , 1 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 0 ] N_6=[1,1,1,1,0,0,1,0,0,0] N6=[1,1,1,1,0,0,1,0,0,0]
N i N_i Ni就是后文auto encoder中的 x i x_i xi

一阶相似度:有监督部分
L 1 s t = ∑ i , j = 1 n s i , j ∣ ∣ y i ( K ) − y j ( K ) ∣ ∣ 2 2 = ∑ i , j = 1 n s i , j ∣ ∣ y i − y j ∣ ∣ 2 2 L_{1st}=\sum_{i,j=1}^ns_{i,j}||y_i^{(K)}-y_j^{(K)}||_2^2=\sum_{i,j=1}^ns_{i,j}||y_i-y_j||_2^2 L1st=i,j=1∑nsi,j∣∣yi(K)−yj(K)∣∣22=i,j=1∑nsi,j∣∣yi−yj∣∣22
s i , j s_{i,j} si,j是两个点的一阶相似度,如果两点不相连,则该项为0
y i ( K ) , y j ( K ) y_i^{(K)},y_j^{(K)} yi(K),yj(K)是两个点的embedding
如果一阶相似度不为零,那么我们希望 y i ( K ) − y j ( K ) y_i^{(K)}-y_j^{(K)} yi(K)−yj(K)要尽可能的小才能最小化loss
二阶相似度:无监督部分
L 2 n d = ∑ i = 1 n ∣ ∣ ( x ^ i − x i ) ⊙ b i ∣ ∣ 2 2 = ∣ ∣ ( X ^ − X ) ⊙ B ∣ ∣ F 2 L_{2nd}=\sum_{i=1}^n||(\hat x_i-x_i)\odot b_i||_2^2=||(\hat X-X)\odot B||_F^2 L2nd=i=1∑n∣∣(x^i−xi)⊙bi∣∣22=∣∣(X^−X)⊙B∣∣F2
这里的X是二阶相似度,也是要尽可能小才能最小化

细节二 :自编码器
输入=[K,|V|] #K=batch size, |V|=node size
#encoder
encode1:[|V|,s1] #输出=[K,|V|]×[|V|,s1]=[K,s1]
encode2:[s1,s2] #输出=[K,s1]×[s1,s2]=[K,s2]
#decoder
decode1:[s2,s1]#输出=[K,s2]×[s2,s1]=[K,s1]
decode2:[s1,|V|]#输出=[K,s1]×[s1,|V|]=[K,|V|]还原回原来维度的大小
细节三:网络稀疏性处理
在实际的网络过程中,点的规模比较大,边比较少,会存在网络稀疏性问题
调大网络的邻接矩阵非零项对应的loss值
If s i j = 0 , b i j = 1 , else b i j = β > 1 \text{If } s_{ij}=0, b_{ij}=1, \text{else } b_{ij}=β>1 If sij=0,bij=1,else bij=β>1
通俗的讲,本来咱们训练模型,是让模型知道那些地方该是1,那些地方该是0,当然是0的地方不重要,因为很多地方都是0,因此学习哪些地方是1比较重要,但模型比较笨,会学错,我们把1的位置给它乘上一个惩罚因子 β > 1 \beta>1 β>1,当模型在1的位置学习错误loss就会变大很多,因为这个 β = b \beta=b β=b在 L 2 n d L_{2nd} L2nd里面是乘法关系, β = b \beta=b β=b越大, L 2 n d L_{2nd} L2nd就越大。
细节四:目标函数
L 1 s t L_{1st} L1st:一阶相似度损失函数
L 2 n d L_{2nd} L2nd:二阶相似度损失函数
L r e g L_{reg} Lreg:正则化项,是L2 norm
L r e g = 1 2 ∑ k = 1 K ( ∣ ∣ W ( k ) ∣ ∣ F 2 + ∣ ∣ W ^ ( k ) ∣ ∣ F 2 ) L_{reg}=\cfrac{1}{2}\sum_{k=1}^K(||W^{(k)}||_F^2+||\hat W^{(k)}||_F^2) Lreg=21k=1∑K(∣∣W(k)∣∣F2+∣∣W^(k)∣∣F2)
B B B:网络稀疏性矩阵
因此,整体的损失函数可以写为:
L m i x = L 2 n d + α L 1 s t + μ L r e g (1) L_{mix}=L_{2nd}+\alpha L_{1st}+\mu L_{reg}\tag1 Lmix=L2nd+αL1st+μLreg(1)
细节五:优化公式推导
将公式1展开:
L m i x = ∣ ∣ ( X ^ − X ) ⊙ B ∣ ∣ F 2 + α ∑ i , j = 1 n s i , j ∣ ∣ y i − y j ∣ ∣ 2 2 + μ L r e g L_{mix}=||(\hat X-X)\odot B||_F^2+\alpha \sum_{i,j=1}^ns_{i,j}||y_i-y_j||_2^2+\mu L_{reg} Lmix=∣∣(X^−X)⊙B∣∣F2+αi,j=1∑nsi,j∣∣yi−yj∣∣22+μLreg
可以看到 W ^ ( k ) \hat W^{(k)} W^(k)是Decoder过程的参数,和生成隐层向量的一阶相似度无关,所以:
D e c o d e r : ∂ L m i x ∂ W ^ ( k ) = ∂ L 2 n d ∂ W ^ ( k ) + μ ∂ L r e g ∂ W ^ ( k ) Decoder:\cfrac{\partial L_{mix}}{\partial \hat W^{(k)}}=\cfrac{\partial L_{2nd}}{\partial \hat W^{(k)}}+\mu \cfrac{\partial L_{reg}}{\partial \hat W^{(k)}} Decoder:∂W^(k)∂Lmix=∂W^(k)∂L2nd+μ∂W^(k)∂Lreg
E n c o d e r : ∂ L m i x ∂ W ( k ) = ∂ L 2 n d ∂ W ( k ) + α ∂ L 1 s t ∂ W ( k ) + μ ∂ L r e g ∂ W ( k ) Encoder:\cfrac{\partial L_{mix}}{\partial W^{(k)}}=\cfrac{\partial L_{2nd}}{\partial W^{(k)}}+\alpha \cfrac{\partial L_{1st}}{\partial W^{(k)}}+\mu \cfrac{\partial L_{reg}}{\partial W^{(k)}} Encoder:∂W(k)∂Lmix=∂W(k)∂L2nd+α∂W(k)∂L1st+μ∂W(k)∂Lreg
可以看到上面两个公式Decoder中一阶相似度对 W ^ ( k ) \hat W^{(k)} W^(k)求偏导消失了,上面两个式子中 k = 1 , . . . , K k=1,...,K k=1,...,K
看其中一项应用链式法则求导:
∂ L 2 n d ∂ W ^ ( k ) = ∂ L 2 n d ∂ X ^ ⋅ ∂ X ^ ∂ W ^ ( k ) \cfrac{\partial L_{2nd}}{\partial \hat W^{(k)}}=\cfrac{\partial L_{2nd}}{\partial \hat X}\cdot \cfrac{\partial \hat X}{\partial \hat W^{(k)}} ∂W^(k)∂L2nd=∂X^∂L2nd⋅∂W^(k)∂X^
对矩阵的求导:
∂ L 2 n d ∂ X ^ = 2 ( X ^ − X ) ⊙ B \cfrac{\partial L_{2nd}}{\partial \hat X}=2(\hat X-X)\odot B ∂X^∂L2nd=2(X^−X)⊙B
L 1 s t = ∑ i , j = 1 n s i , j ∣ ∣ y i − y j ∣ ∣ 2 2 = 2 t r ( Y T L Y ) L_{1st}= \sum_{i,j=1}^ns_{i,j}||y_i-y_j||_2^2=2tr(Y^TLY) L1st=i,j=1∑nsi,j∣∣yi−yj∣∣22=2tr(YTLY)
其中tr是矩阵的秩,L是拉普拉斯矩阵(具体在第六篇GCN中介绍),这个用链式法则进行求导:
∂ L 1 s t ∂ W ( k ) = ∂ L 1 s t ∂ Y ⋅ ∂ Y ∂ W ( k ) \cfrac{\partial L_{1st}}{\partial W^{(k)}}=\cfrac{\partial L_{1st}}{\partial Y}\cdot\cfrac{\partial Y}{\partial W^{(k)}} ∂W(k)∂L1st=∂Y∂L1st⋅∂W(k)∂Y
∂ L 1 s t ∂ Y = 2 ( L + L T ) ⋅ Y \cfrac{\partial L_{1st}}{\partial Y}=2(L+L^T)\cdot Y ∂Y∂L1st=2(L+LT)⋅Y
对于新加入点的处理:将新节点的邻居信息找到,丢如AE,即可得到新节点的embedding表示。如果新节点没有任何邻居,可以用节点上的属性对节点进行embedding,例如节点是一个商品,那么可以根据商品的类别、生产日期等属性去直接embedding。
细节六:时间复杂度
单点的前向传播 O ( 1 ) O(1) O(1),看下这个玩意怎么来
由于是单点,图如果有n个节点,所以输入是 [ 1 , n ] [1,n] [1,n],我们要转换为d维的向量,那么参数维度应该是: [ n , d ] [n,d] [n,d],最后得到结果的维度是 [ 1 , d ] [1,d] [1,d],这个过程的相当于矩阵相乘,其时间复杂度为:
[ 1 , n ] × [ n , d ] = [ 1 , d ] → O ( n d ) [1,n]\times[n,d]=[1,d]\rightarrow O(nd) [1,n]×[n,d]=[1,d]→O(nd)
当然在下图的AE结构中
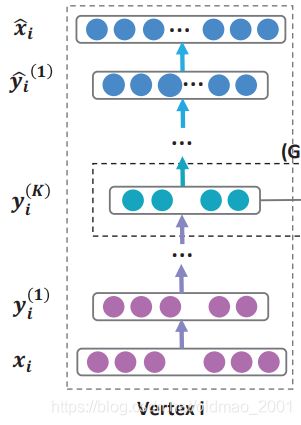
其实如果是有 k k k层神经元,那么时间复杂度应该是 O ( k n d ) O(knd) O(knd),但是由于 k k k是常数,那么 k k k可以省略。
上面提到的输入是 [ 1 , n ] [1,n] [1,n],实际上每个点不会和其它所有点相邻,而是和部分点相邻,我们假定其最多有 c c c个相邻点,即假设 max degree = c \text{max degree}=c max degree=c,我们可以用稀疏向量存储输入,所以在矩阵相乘的时候,不用做 n d nd nd次,只用对非零项进行相乘,因此有:
O ( n d ) → O ( c d ) → O ( 1 ) O(nd)\rightarrow O(cd)\rightarrow O(1) O(nd)→O(cd)→O(1)
这样就推导出来一个点的前向传播时间复杂度为: O ( 1 ) O(1) O(1)
总的时间复杂度
one iteration:
n次前向传播(相当于n个点进行前向传播), O ( 1 ) × n = O ( n ) O(1)\times n=O(n) O(1)×n=O(n)
L 2 n d L_{2nd} L2nd计算,如果用稀疏向量存储,其时间复杂度为: O ( n c ) O(nc) O(nc),看下怎么来
原公式 X X X维度是 n × n n\times n n×n的, X ^ − X \hat X-X X^−X维度还是 n × n n\times n n×n,然后对 n × n n\times n n×n矩阵求L2 norm,那么其时间复杂就是 O ( n 2 ) O(n^2) O(n2),如果X也用稀疏向量存储,时间复杂度就变成了 O ( n c ) O(nc) O(nc)(为什么不是c的平方?)
L 1 s t L_{1st} L1st计算, ( y i − y j ) 2 = O ( d ) (y_i-y_j)^2=O(d) (yi−yj)2=O(d),sum一共 n × c n\times c n×c项,总共 O ( n c d ) O(ncd) O(ncd)
先看 y i , y j y_i,y_j yi,yj都是 1 × d 1×d 1×d维的embedding表示,那么两个向量相减,还是 1 × d 1×d 1×d维,然后平方,时间复杂度是: O ( d ) O(d) O(d),然后看求和项,可以看到一个点最多有 c c c个邻居,两层循环,一个从1到 n n n,一个只需要1到 c c c就可以,所以,求和 ∑ i , j = 1 n \sum_{i,j=1}^n ∑i,j=1n一共是 n × c n\times c n×c项;总共的时间复杂度为: O ( n c d ) O(ncd) O(ncd)
整个iteration的时间复杂度为:
O ( n ) + O ( n c ) + O ( n c d ) → O ( n c d ) O(n)+O(nc)+O(ncd)\rightarrow O(ncd) O(n)+O(nc)+O(ncd)→O(ncd)
I I I iterations: O ( n c d I ) O(ncdI) O(ncdI)
实验设置与分析

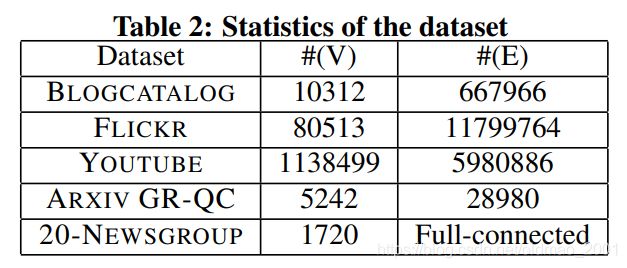
datasets 数据集:
social,citation,language
Full-connected:clique
TF-IDF(Term Frequency-inverse Document Frequency)是一种针对关键词的统计分析方法,用于评估一个词对一个文件集或者一个语料库的重要程度。一个词的重要程度跟它在文章中出现的次数成正比,跟它在语料库出现的次数成反比。这种计算方式能有效避免常用词对关键词的影响,提高了关键词与文章之间的相关性。
代码复现
准备工作
项目环境配置
·Python 3.6
.torch 1.3.1
·numpy 1.18.1
·sklearn 0.23.1
·jupyter notebook
数据集:cora_edgelist.txt
额外要安装的包:pip install networkx
或者找:networkx-2.5-py3-none-any.whl手工安装
原文在实现的过程中,用到了预训练向量,复现没有用。
main
实现思路
1.设置模型参数
2.读图,可以打印测试,两个数字一样就没错

3.sdne模型实现
4.模型训练
5.结果展示和可视化
具体代码
import torch
import torch.optim as optim
from argparse import ArgumentParser, ArgumentDefaultsHelpFormatter
from torch.utils.data.dataloader import DataLoader
import utils
from data import dataset
from models import model
import numpy as np
# 1.设置模型参数
# 1)设置模型参数设置模型超参数,如损失函数中的alpha、beta(具体看公式),神经网络的相关参数如batch size、epoch、learning rate、dropout rate等
# 2)输入输出
# 输入文件./data/cora/cora_edgelist.txt
# 输出文件./data/cora/Vec.emb
def parse_args():
# 使用parser加载信息
parser = ArgumentParser(formatter_class=ArgumentDefaultsHelpFormatter,
conflict_handler='resolve')
# 输入文件
parser.add_argument('--input', default='./data/cora/cora_edgelist.txt',
help='Input graph file')
# 训练结果embedding输出文件
parser.add_argument('--output', default='./data/cora/Vec.emb',
help='Output representation file')
# 并行参数
parser.add_argument('--workers', default=8, type=int,
help='Number of parallel processes.')
# 处理有/无权图
parser.add_argument('--weighted', action='store_true', default=False,
help='Treat graph as weighted')
# epoch数量
parser.add_argument('--epochs', default=100, type=int,
help='The training epochs of SDNE')
# dropout比例值
parser.add_argument('--dropout', default=0.5, type=float,
help='Dropout rate (1 - keep probability)')
# 权重衰减系数,未使用
parser.add_argument('--weight-decay', type=float, default=5e-4,
help='Weight for L2 loss on embedding matrix')
# 学习率设置
parser.add_argument('--lr', default=0.001, type=float,
help='learning rate')
# 模型参数,一阶相似度和二阶相似度之间的比重
parser.add_argument('--alpha', default=1e-2, type=float,
help='alhpa is a hyperparameter in SDNE')
# 图的稀疏性问题,论文中的参数beta, 侧重学习邻接矩阵中为1的值
parser.add_argument('--beta', default=5., type=float,
help='beta is a hyperparameter in SDNE')
# 未使用
parser.add_argument('--nu1', default=1e-5, type=float,
help='nu1 is a hyperparameter in SDNE')
# 未使用
parser.add_argument('--nu2', default=1e-4, type=float,
help='nu2 is a hyperparameter in SDNE')
# batch大小
parser.add_argument('--bs', default=100, type=int,
help='batch size of SDNE')
# 自编码器第一层神经元个数
parser.add_argument('--nhid0', default=1000, type=int,
help='The first dim')
# 自编码器第二层神经元个数,也是最终的embedding维度
parser.add_argument('--nhid1', default=128, type=int,
help='The second dim')
# 学习率步长设置
parser.add_argument('--step_size', default=10, type=int,
help='The step size for lr')
# 学习率gamma值设置,adam优化器
parser.add_argument('--gamma', default=0.9, type=int,
help='The gamma for lr')
args = parser.parse_args()
return args
if __name__ == '__main__':
args = parse_args() # 读取参数
# 2.从./data/cora/cora_edgelist.txt读取图数据
G, Adj, Node = dataset.Read_graph(args.input)
# 3.SDNE模型实现
# ./models/model.py中的MNN类,基于pytorch实现的论文中的AE
model = model.MNN(Node, args.nhid0, args.nhid1, args.dropout, args.alpha)
# # Adam算法优化模型参数
opt = optim.Adam(model.parameters(), lr=args.lr)
# 设置模型的学习率等超参
scheduler = torch.optim.lr_scheduler.StepLR(opt, step_size=args.step_size, gamma=args.gamma)
Data = dataset.Dataload(Adj, Node)
# 按batchsize将训练样本分组
Data = DataLoader(Data, batch_size=args.bs, shuffle=True, )
# 4.模型训练
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # 设置选用gpu或cpu训练
model = model.to(device)
model.train()
# 共训练epoch次数
for epoch in range(1, args.epochs + 1):
loss_sum, loss_L1, loss_L2, loss_reg = 0, 0, 0, 0
# 每次训练组数:batchsize
for index in Data:
adj_batch = Adj[index]
adj_mat = adj_batch[:, index]
# 将邻接矩阵中的为0项设为1,为1项设为beta,这里对应模型细节三,原文公式3
b_mat = torch.ones_like(adj_batch)
b_mat[adj_batch != 0] = args.beta
# 在做BP之前将gradients置0因为是累加的
opt.zero_grad()
L_1st, L_2nd, L_all = model(adj_batch, adj_mat, b_mat)
L_reg = 0
for param in model.parameters():
L_reg += args.nu1 * torch.sum(torch.abs(param)) + args.nu2 * torch.sum(param * param)
# 将损失值和正则化项加在一起构成最终的损失函数
Loss = L_all + L_reg
# 反向传播,计算梯度
Loss.backward()
opt.step()
# 记录相应部分loss值
loss_sum += Loss
# 一阶相似度的loss值
loss_L1 += L_1st
# 二阶相似度的loss值
loss_L2 += L_2nd
# 正则化项loss值
loss_reg += L_reg
scheduler.step(epoch)
# 每次epoch输出训练情况,loss值等
# print("The lr for epoch %d is %f" %(epoch, scheduler.get_lr()[0]))
print("loss for epoch %d is:" % epoch)
print("loss_sum is %f" % loss_sum)
print("loss_L1 is %f" % loss_L1)
print("loss_L2 is %f" % loss_L2)
print("loss_reg is %f" % loss_reg)
model.eval()
embedding = model.savector(Adj)
outVec = embedding.detach().numpy()
np.savetxt(args.output, outVec)
model
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.parameter import Parameter
from torch.nn.modules.module import Module
# 继承自Module
# 要实现__init__(声明)、forward(前向传播)
class MNN(nn.Module):
# node_size为输入的向量的长度
# nhid0为编码器第一层隐藏层大小
# nhid1为编码器第二层隐藏层大小
# 由于AE是对称的,解码器隐藏层大小从编码器可以获得
# droput和alpha是参数
def __init__(self, node_size, nhid0, nhid1, droput, alpha):
# 声明神经网络都有哪些层
# 这里的结构是:输入-encode0-encode1-decode0-decode1-输出
# 于是如果我们输入的向量的长度为node_size,那么每一层神经元的个数分别是
# 假设我们一次输入的batch_size = K,相当于K个顶点
# 输入 = [K, node_size]
super(MNN, self).__init__()
# 输出计算过程的规律是去掉中间两个相同列和行。
# encode0: [node_size, nhid0], 这一步输出 = [K, node_size] * [node_size, nhid0] = [K, nhid0]
self.encode0 = nn.Linear(node_size, nhid0)
# encode1: [nhid0, nhid1], 这一步输出 = [K, nhid0] * [nhid0, nhid1] = [K, nhid1]
self.encode1 = nn.Linear(nhid0, nhid1)
# decode0: [nhid1, nhid0], 这一步输出 = [K, nhid1] * [nhid1, nhid0] = [K, nhid0]
self.decode0 = nn.Linear(nhid1, nhid0)
# decode1: [nhid0, node_size], 这一步输出 = [K, nhid0] * [nhid0, node_size] = [K, node_size]
# 自编码器希望最终的输出尽可能与输入相等(reconstruction error最小化),维度大小当然一样:K*node_size
self.decode1 = nn.Linear(nhid0, node_size)
self.droput = droput
self.alpha = alpha # 原文公式5
def forward(self, adj_batch, adj_mat, b_mat):
# __init__中声明的神经网络的架构实现,层与层的连接
# 激活函数使用的是leaky_relu
# 这里的结构是:输入-encode0-encode1-decode0-decode1-输出
t0 = F.leaky_relu(self.encode0(adj_batch))
t0 = F.leaky_relu(self.encode1(t0))
# 这个中间隐藏层的输出结果就是我们最终要保留的node embedding,保存到embedding这个变量,t0继续更新
embedding = t0
t0 = F.leaky_relu(self.decode0(t0))
t0 = F.leaky_relu(self.decode1(t0)) # 这里t0是最后Decoder还原的结果,对应原文的x hat
embedding_norm = torch.sum(embedding * embedding, dim=1, keepdim=True) # 维度大小为Batchsize*1
# 一阶相似度的loss值
L_1st = torch.sum(adj_mat * (embedding_norm - 2 * torch.mm(embedding, torch.transpose(embedding, dim0=0, dim1=1)) + torch.transpose(embedding_norm, dim0=0, dim1=1)))
# 二阶相似度的loss值
L_2nd = torch.sum(((adj_batch - t0) * b_mat) * ((adj_batch - t0) * b_mat))
return L_1st, self.alpha * L_2nd, L_1st + self.alpha * L_2nd
def savector(self, adj):
t0 = self.encode0(adj)
t0 = self.encode1(t0)
return t0
损失与代码的对应
先看代码
# 一阶相似度的loss值
L_1st = torch.sum(adj_mat * (embedding_norm - 2 * torch.mm(embedding, torch.transpose(embedding, dim0=0, dim1=1)) + torch.transpose(embedding_norm, dim0=0, dim1=1)))
看公式:一阶相似度
L 1 s t = ∑ i , j = 1 n s i , j ∣ ∣ y i ( K ) − y j ( K ) ∣ ∣ 2 2 = ∑ i , j = 1 n s i , j ∣ ∣ y i − y j ∣ ∣ 2 2 L_{1st}=\sum_{i,j=1}^ns_{i,j}||y_i^{(K)}-y_j^{(K)}||_2^2=\sum_{i,j=1}^ns_{i,j}||y_i-y_j||_2^2 L1st=i,j=1∑nsi,j∣∣yi(K)−yj(K)∣∣22=i,j=1∑nsi,j∣∣yi−yj∣∣22
s i , j s_{i,j} si,j是两个点的一阶相似度,如果两点不相连,则该项为0
y i ( K ) , y j ( K ) y_i^{(K)},y_j^{(K)} yi(K),yj(K)是两个点的embedding
把第 i , j i,j i,j两个点进行展开:
L 1 s t i , j = ∑ p = 1... k ∣ ∣ y i − y j ∣ ∣ 2 2 = ( y i 1 − y j 1 ) 2 + ( y i 2 − y j 2 ) 2 + . . . + ( y i k − y j k ) 2 L_{1st_{i,j}}=\sum_{p=1...k}||y_i-y_j||_2^2\\ =(y_{i1}-y_{j1})^2+(y_{i2}-y_{j2})^2+...+(y_{ik}-y_{jk})^2 L1sti,j=p=1...k∑∣∣yi−yj∣∣22=(yi1−yj1)2+(yi2−yj2)2+...+(yik−yjk)2
展开:
L 1 s t i , j = ∑ p = 1... k y i p 2 − 2 ( y i 1 y j 1 + y i 2 y j 2 + . . . + y i k y j k ) + ∑ p = 1... k y j p 2 (2) L_{1st_{i,j}}=\sum_{p=1...k}y_{ip}^2-2(y_{i1}y_{j1}+y_{i2}y_{j2}+...+y_{ik}y_{jk})+\sum_{p=1...k}y_{jp}^2\tag2 L1sti,j=p=1...k∑yip2−2(yi1yj1+yi2yj2+...+yikyjk)+p=1...k∑yjp2(2)
L2 Norm的平方是根据下面的公式进行推算:
∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + . . . + ∣ x n ∣ 2 ) 1 / 2 ||x||_2=(|x_1|^2+|x_2|^2+...+|x_n|^2)^{1/2} ∣∣x∣∣2=(∣x1∣2+∣x2∣2+...+∣xn∣2)1/2
∣ ∣ x ∣ ∣ 2 2 = ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + . . . + ∣ x n ∣ 2 ||x||_2^2=|x_1|^2+|x_2|^2+...+|x_n|^2 ∣∣x∣∣22=∣x1∣2+∣x2∣2+...+∣xn∣2
上面的公式2,第一项对应的代码为:
embedding_norm = torch.sum(embedding * embedding, dim=1, keepdim=True) # 维度大小为Batchsize*1
embedding 是中间维度表示其大小为:Batchsize(记为 n n n)×embedding 维度(文中用的是128,记为 k k k),即维度为 n × k n×k n×k
[ y 11 ⋯ y 1 k ⋮ ⋯ ⋮ y n 1 ⋯ y n k ] \begin{bmatrix} y_{11} & \cdots&y_{1k} \\ \vdots & \cdots &\vdots \\ y_{n1} & \cdots& y_{nk} \end{bmatrix} ⎣⎢⎡y11⋮yn1⋯⋯⋯y1k⋮ynk⎦⎥⎤
embedding × embedding:
[ y 11 2 ⋯ y 1 k 2 ⋮ ⋯ ⋮ y n 1 2 ⋯ y n k 2 ] \begin{bmatrix} y_{11}^2 & \cdots&y_{1k}^2 \\ \vdots & \cdots &\vdots \\ y_{n1}^2 & \cdots& y_{nk}^2 \end{bmatrix} ⎣⎢⎡y112⋮yn12⋯⋯⋯y1k2⋮ynk2⎦⎥⎤
然后dim=1, keepdim=True表示按第二个维度进行累加求和,变成维度为n×1:
[ y 11 2 + ⋯ + y 1 k 2 ⋮ + ⋯ + ⋮ y n 1 2 + ⋯ + y n k 2 ] = [ ∑ p = 1... k y 1 p 2 ⋮ ∑ p = 1... k y n p 2 ] \begin{bmatrix} y_{11}^2 + \cdots+y_{1k}^2 \\ \vdots + \cdots +\vdots \\ y_{n1}^2 + \cdots+ y_{nk}^2 \end{bmatrix}=\begin{bmatrix} \sum_{p=1...k}y_{1p}^2 \\ \vdots \\ \sum_{p=1...k}y_{np}^2 \end{bmatrix} ⎣⎢⎡y112+⋯+y1k2⋮+⋯+⋮yn12+⋯+ynk2⎦⎥⎤=⎣⎢⎡∑p=1...ky1p2⋮∑p=1...kynp2⎦⎥⎤
第三项对应的代码为:
torch.transpose(embedding_norm, dim0=0, dim1=1)
[ ∑ p = 1... k y 1 p 2 ⋯ ∑ p = 1... k y n p 2 ] \begin{bmatrix} \sum_{p=1...k}y_{1p}^2 & \cdots &\sum_{p=1...k}y_{np}^2 \end{bmatrix} [∑p=1...ky1p2⋯∑p=1...kynp2]
中间项对应的代码为:
-2 * torch.mm(embedding, torch.transpose(embedding, dim0=0, dim1=1))
实际上是 n × k n×k n×k和 k × n k×n k×n的维度矩阵相乘:
− 2 [ y 11 ⋯ y 1 k ⋮ ⋯ ⋮ y n 1 ⋯ y n k ] ⋅ [ y 11 ⋯ y n 1 ⋮ ⋯ ⋮ y 1 k ⋯ y n k ] -2\begin{bmatrix} y_{11} & \cdots&y_{1k} \\ \vdots & \cdots &\vdots \\ y_{n1} & \cdots& y_{nk} \end{bmatrix}\cdot\begin{bmatrix} y_{11} & \cdots&y_{n1} \\ \vdots & \cdots &\vdots \\ y_{1k} & \cdots& y_{nk} \end{bmatrix} −2⎣⎢⎡y11⋮yn1⋯⋯⋯y1k⋮ynk⎦⎥⎤⋅⎣⎢⎡y11⋮y1k⋯⋯⋯yn1⋮ynk⎦⎥⎤
dataset
import networkx as nx
import numpy as np
from torch.utils import data
from torch.utils.data import DataLoader
import torch
def Read_graph(file_name):
#numpy的loadtxt要求文本文件中的每一行必须含有相同的数据;delimiter分隔符默认是空格;类型是numpy array
edge = np.loadtxt(file_name).astype(np.int32)
# 得到图中点的最小和最大编号,.min()返回数组中所有元素最小的
min_node, max_node = edge.min(), edge.max()
# Node表示图上一共有多少个顶点,如果标号index是从0开始,那么顶点数 = max_node + 1
if min_node == 0:
Node = max_node + 1
else:
Node = max_node
# 这里面使用networkx将图的信息存入
G = nx.Graph()
# Adj就是图的邻接表矩阵,是一个n*n大小的numpy矩阵,这里n是顶点的个数
Adj = np.zeros([Node, Node], dtype=np.int32)
# 遍历边的文件,将每条边存入networkx的图G,以及邻接矩阵Adj所对应的位置(i, j)
for i in range(edge.shape[0]):
G.add_edge(edge[i][0], edge[i][1])
if min_node == 0:# 处理标号index是从0开始的情况
Adj[edge[i][0], edge[i][1]] = 1
Adj[edge[i][1], edge[i][0]] = 1
else:
Adj[edge[i][0] - 1, edge[i][1] - 1] = 1
Adj[edge[i][1] - 1, edge[i][0] - 1] = 1
# 转化成tensor
Adj = torch.FloatTensor(Adj)
return G, Adj, Node
# 继承自pytorch中的data.Dataset类,为了后面batch训练方便
class Dataload(data.Dataset):
def __init__(self, Adj, Node):
self.Adj = Adj
self.Node = Node
def __getitem__(self, index):
return index
# adj_batch = self.Adj[index]
# adj_mat = adj_batch[index]
# b_mat = torch.ones_like(adj_batch)
# b_mat[adj_batch != 0] = self.Beta
# return adj_batch, adj_mat, b_mat
def __len__(self):
return self.Node
if __name__ == '__main__':
G, Adj, Node = Read_graph('./karate/karate.edgelist')
Data = Dataload(Adj, Node)
Test = DataLoader(Data, batch_size=20, shuffle=True)
for index in Test:
adj_batch = Adj[index]
adj_mat = adj_batch[:, index]
b_mat = torch.ones_like(adj_batch)
b_mat[adj_batch != 0] = 5
print(b_mat)
draw_cora
用sklearn的TSNE
问题
一阶相似度代码中,为什么是:torch.transpose(embedding_norm, dim0=0, dim1=1)
为什么每次epoch要重置梯度?