深度之眼Paper带读笔记GNN.04.metapath2vec

前言

本课程来自深度之眼，部分截图来自课程视频。

文章标题：metapath2vec:Scalable Representation Learning for Heterogeneous Networks
结构化深度网络特征表示
作者：Yuxiao Dong.etc（董玉箫？）
单位：Microsoft Research
发表会议及时间：KDD 2017（KDD比较偏实验）
公式输入请参考：在线Latex公式

论文结构

1. Abstract：提出基于传统图的图表征学习算法无法很好的应用到点和边有多个类型的异质图，引出本文的算法metapath2vec（++：这个版本就是加强版）。
2. Introduction：之前的算法多集中在研究同质网络如deepwalk、LINE、node2vec等，引出异质图中的多类型的点和边所存在的广泛应用，以及难点和挑战性。
3. Related Work：基于邻接表矩阵分解的网络表征算法（如果不降维的话）计算开销大，效果不理想；比较了基于deepwalk、LINE、node2vec等同质图算法。
4. Problem Definition：定义异质图上的网络表征学习，表示metapath（这个是异质图的公认定义）。
5. Metapath2vect：论文算法的模型部分，异质图上的skip2gram算法以及基于metapath的随机游走算法。
6. Metapath2vec++：异质图上的负采样算法，异质图学习算法的完整框架。
7. Dataset and Baselines：选取Aminer和DBIS数据集以及DeepWalk、LINE、PTE、邻接表分解等baselines 。
8. Effectiveness：实验探究模型有效性：节点分类、节点聚类、点相似性、可视化等，参数讨论。
9. Conclusion：总结提出了一种基于异质图的神经网路框架。
   

基础知识补充

NMI指标（归一化互信息或标准化互信息Normal Mutual Information）：排序指标，NMI常用在聚类中，度量2个聚类结果的相近程度，值越大越好。用下面的图来看具体例子。

Purity as an external evaluation criterion for cluster quality. Majority class and number of members of the majority class for the three clusters are:
x, 5(cluster1);
o, 4(cluster 2);
◇, 3(cluster 3).
Purity is (1/17)×(5+4+3)= 0.71.

比如标准结果是图中的叉叉圈圈块块，分别用1,2,3表示，上面三个聚类的标准结果为：
B=[121111 122223 11333]
如果我们的预测结果是：
A=[111111 222222 33333]
问题：衡量我们的预测结果和标准结果有多大的区别，若我们的预测结果和标准结果的差不多，NMI指标应该为1，若我们的预测做出来的结果很差，NMI指标应该趋近于0。

---

【百度百科】互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。

---

NMI先要算MI（互信息Mutual Information）指标：
$$I(X;Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\text{log}\left(\frac{p(x,y)}{p(x)p(y)}\right)$$
$p(x,y)$是$x$和$y$的联合分布概率，例如：$x=1,y=1$在结果A和B中出现了5次，总体样本个数为17：
$$\begin{gathered} B=[\underline{1}2\underline{1111}12222311333] \\ A=[\underline{1}1\underline{1111}22222233333] \end{gathered}$$
那么：
$$\begin{gathered} p(1,1)=5/17,p(1,2)=1/17,p(1,3)=0; \\ p(2,1)=1/17,p(2,2)=4/17,p(2,3)=1/17; \\ p(3,1)=2/17,p(3.2)=0,p(3,3)=3/17; \end{gathered}$$
分母$p(x)$为$x$的边缘概率函数，$p(y)$为$y$的边缘概率函数，$x$和$y$分别来自于A和B中的分布，所以即使$x=y$时，$p(x)$和$p(y)$也可能是不一样的。
对$p(x)$：
$$p(1)=6/17,p(2)=6/17,p(3)=5/17$$
对$p(y)$：
$$p(1)=8/17,p(2)=5/17,P(3)=4/17$$
然后将MI进行归一化：
$$NMI(X,Y)=\frac{2MI(X,Y)}{H(X)+H(Y)}\text{\hspace{1em}(1)}$$
上式中$H(X),H(Y)$分别是$X,Y$的熵：
$$\begin{gathered} H(X)=-\sum _{i=1}^{|X|}P(i)\text{log}(P(i)) \\ H(Y)=-\sum _{j=1}^{|Y|}{P}^{\prime }(j)\text{log}(P^{\prime }(j)) \end{gathered}$$
对于上面的例子，根据公式计算嫡如下：
$$\begin{gathered} H(X)=P(1){\text{log}}_2(P(1))+P(2){\text{log}}_2(P(2))+P(3){\text{log}}_2(P(3)) \\ H(Y)=P^{\prime }(1){\text{log}}_2(P^{\prime }(1))+P{(}^{\prime }2){\text{log}}_2(P^{\prime }(2))+P^{\prime }(3){\text{log}}_2(P^{\prime }(3)) \end{gathered}$$
结合上面的结果代入公式1即可得到NMI结果。

研究背景

网络表征学习：从传统的特征工程过渡到基于深度学习的算法

node attribute inference：节点属性预测
community detection：社群聚类
similarity search：相似搜索
link prediction：相关性预测
social recommendation：社交推荐
本论文基于random walk（红框）+skip2gram（蓝框）的框架

本文研究对象是异质图（深度类开山之作），当然不会像知识图谱中节点和边的类型非常多，这里研究 的异质图节点类型就几种，例如下图中有时间、地点、名称等

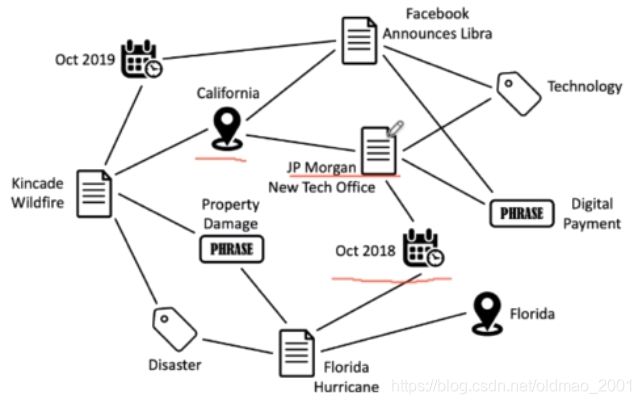
下面左图节点有3种类型：author、paper、venue。右图节点有2种类型。

总的来说，一般图有如下几种：同质图（简单图）、

图类型	节点类型	边类型
HOMOGENEOUS	1	1
BIPARTITE	2	1
K-PARTITE	k	k-1
SIGNED	1	2
LABELED	k	l
STAR	k	k-1

本文研究的对象

An academic network：有四个类型的点（注意每个类型点的首字母用在meta path上），边的类型也有几种，例如org和author之间是雇佣关系，author和author之间还有橙色的虚线表示合作关系，文章和文章之间有红色箭头代表引用关系（有向），文章和会议是发表在的关系，作者和文章是发表的关系。
右边是定义的meta path，是人工定义的，就是我们想要关注的那些信息。

注意meta-path的语意：比如APA：两个作者（Authors）共同合作了一篇论文。

模型框架

对于同质图是直接用k维向量来进行表征。

对于异质图，本文将向量按节点类型进行了切分，然后再分别使用向量表示（下图中的$k_V,k_A,k_O,k_P$）。

下面是metapath2vec++的算法描述：
输入是$G=(V,E,T)$，T表示异质图
花P是自己定义的meta path（就是上面例子的APA之类的东西）
整个算法分成三个函数，一个是初始化，一个是MetaPathRandomWalk，一个是HeterogeneousSkipGram

MP是每个节点的sequence

研究意义

1. 将random walk+skip2gram的框架拓展到异质图，如何在多种类型的节点之间定义节点的上下文从而产生好的训练语料
2. 基于异质图的随机游走算法表达了不同类型节点之间的语义和结构关联
3. 早期研究异质图学习的工作，拓展了关于更多类型的网络的图表示学习研究
4. 引用量500+
5. 早期异质图的网络学习的代表性工作，异质图上的经典baseline
6. 拓展了深度学习研究图的类型，进一步将深度学习领域的模型引入更广泛的图学习

研究成果

Multi-label Classification 节点分类
横坐标百分比代表使用多少比例的数据进行训练
venue node分类结果：

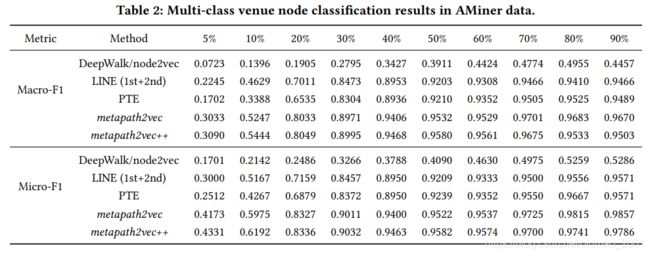
author node分类结果：

超参数对模型有效性实验
w是遍历次数（600最好）
l是遍历深度（60最好）
两个结合起来就是产生w个l长度的sequence。
表征维度d（384最好）

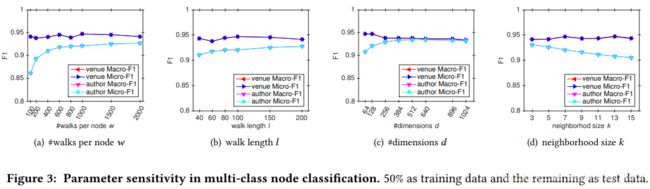
NMI指标的比较：


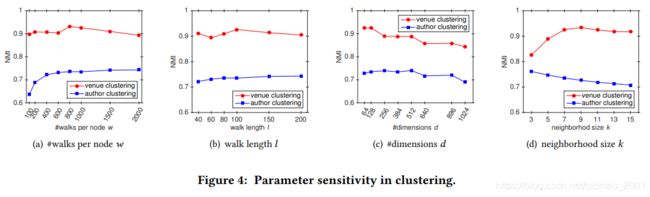
可视化结果：
下图是会议节点t-SNE降维的结果，相同类型节点相同颜色。

下面是用PCA降维，在几个baseline的比较：

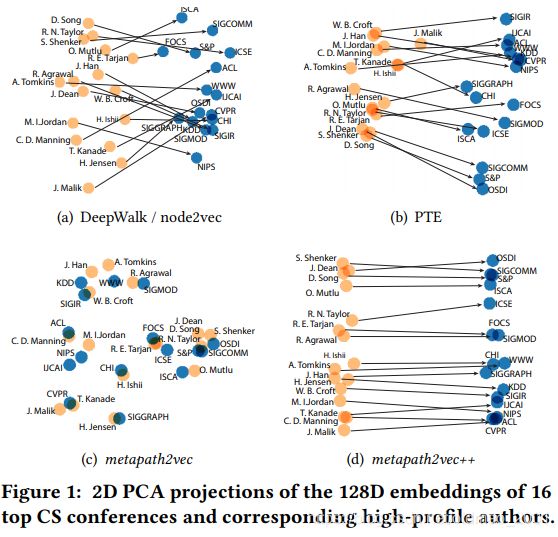
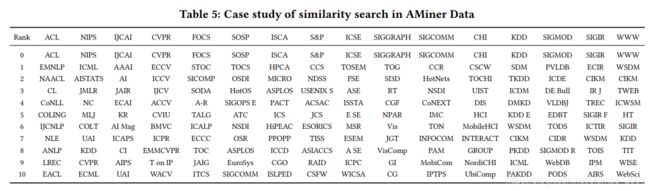
会议节点相似性排名，越相关越靠上：
下面的图是显示当可用资源（线程）变化，模型性能指标的提升效果，可以看到效果不错，基本线性。

论文泛读

摘要核心

1.强调之前的模型研究的是同质网络，无法更好地表达点和边的多样性
2.基于异质图上的meta-path设计random walk算法
3.基于skip2gram框架和负采样算法完成异质图的学习4.通过节点分类、聚类、相似性等任务在Aminer和DBIS两个数据集验证了模型的有效性

论文标题

1. Introduction
2. Problem Definition
3. The merapath2vec framework
   3.1Homogeneous Network Embedding
   3.2 Heterogeneous Network Embedding: metapath2vec
   3.3 metapath2vec++
4. Experiments
   4.1Experimental Setup
   4.2Multi-Class Classification
   4.3 Node Clustering
   4.4 Case Study:Similarity Search
   4.5 Case Study:Visualization
   4.6Scalability
5. Related Work
6. Conclusion

论文精读

metapath2vec详解

挑战性：
1.multiple types of nodes and links 有不同的节点和边
2.difficult to directly apply homogeneous network embedding methods.用同质性网络表征会丢失一部分信息
3.node-neighborhood concept
4.structures and semantics

问题定义

Definition 2.1. A Heterogeneous Network is defined as a graph $G=(V,E,T)$ in which each node $v$ and each link $e$ are associated with their mapping functions $\varphi (v):V\to T_V$ and $\phi (e):E\to T_E$, respectively. $T_V$ and $T_E$ denote the sets of object and relation types, where $|T_V|+|T_E|>2$.
异质图和同质图的定义不一样，多了一个T，实际上在定义里面就是两个函数，表示节点和边的分类到集合的映射。例如：$\varphi (北京大学)=Org$，$\varphi (张三)=Author$
由于是异质图，所以有最后节点和边的类型的和要大于2的约束。
异质图表征的定义和同质图表征的定义一样。
Problem 1. Heterogeneous Network Representation Learning: Given a heterogeneous network $G$, the task is to learn the $d$ dimensional latent representations $X\in R^{|V|\times d},d<<|V|$ that are
able to capture the structural and semantic relations among them.

细节一：Heterogeneous skip-gram

先有word2vec在同质图的应用：DeepWalk&Node2vec
$$\text{arg}\underset{\theta }{\max }\prod _{v\in V}\prod _{c\in N(v)}p(c|v;\theta )$$
目标：要找到一个参数$\theta$使得$v$周围的上下文（或者说邻居）$c$出现的概率最大
本文在这个基础上引入异质性网络，也就是$v$有很多类，就变成了Heterogeneous skip-gram model：
$$\text{arg}\underset{\theta }{\max }\prod _{v\in V}\prod _{t\in T_v}\prod _{c_t\in N_t(v)}p(c_t|v;\theta )$$
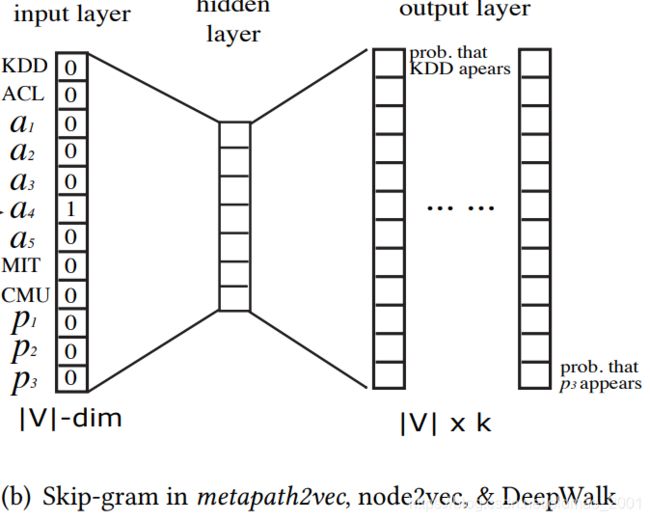
可以看到改动就是中间加了一项连乘：${\prod }_{t\in T_v}$，这个$T_V$就是节点$V$的不同类型的集合，例如：the neighborhood of one author node $a_4$ can be structurally close to other authors
(e.g., $a_2$, $a_3$ & $a_5$), venues (e.g., ACL & KDD), organizations (CMU
& MIT（原文能把MIT放进来不太严谨）), as well as papers (e.g., $p_2$ & $p_3$).。

连乘套路就是加log变连加：
$$\text{arg}\underset{\theta }{\max }\sum _{v\in V}\sum _{t\in T_v}\sum _{c_t\in N_t(v)}\text{log}p(c_t|v;\theta )$$
概率的计算写成公式是(用的softmax)：
$$p(c_t|v;\theta )=\frac{e^{X_{c_t}\cdot X_v}}{{\sum }_{u\in V}{e}^{X_u\cdot X_v}}$$
注意上面这个公式没有对节点$u$进行分类，在metapath2vec++对这个才进行了处理（在细节三种有讲）。
可以看到分母的累加是要遍历所有节点的，这个计算量太大，本文根据skip-gram的优化方法，引入负采样(推导要看LINE论文)：
$$\text{log}\sigma (X_{c_t}\cdot X_v)+\sum _{m=1}^M{E}_{u^m\sim P(u)}[\text{log}\sigma (-X_{u^m}\cdot X_v)],\text{ where }\sigma (x)=\frac{1}{1+e^{-x}}$$

细节二：Meta-Path-Based Random Walks

DeepWalk/Node2vec：随机游走（忽视节点的类型）。
meta-path特点：对称性（一般都对称）

具体定义描述：
1.Given a meta-path scheme，实际上就是上图的抽象表达，从一个节点到下一个节点，只不过节点的类型可以是不一样的。

2.The transition probability at step $i$ is defined as:状态转移矩阵是metapath的核心
下式中$i$代表第$i$个时间步，下标$t$代表节点类型
一共三种情况，第三种最简单，下一个时间步的节点和当前节点不是邻居关系（没有边相连），则取值为0；
第二种情况：下一个时间步的节点和当前节点是邻居节点（有边相连$(v^{i+1},v_t^i)\in E$），但是下一个时间步的节点的类型和我们在metapath中定义的下一个节点类型不一致（$\varphi$功效不记得的同学请往上翻。）则取值为0；
第一种情况：下一个时间步的节点和当前节点是邻居节点（有边相连$(v^{i+1},v_t^i)\in E$），且类型与metapath中定义的类型一致，那么它的转移概率为下一个时间步的节点类型数量分之一，就是概率一样的。

---

感觉老师口误：应该是下一个时间步与当前节点类型相邻的下一个节点类型的节点数量分之一
例如文章类型节点有3个，但是与$a_2$作者这个节点相邻的文章类型节点只有2个：$p_1,p_2$，这里的转移概率为1/2，不是1/3

---

$$p(v^{i+1}|v_t^i,\wp )=\{\begin{array}{ll}& \frac{1}{|N_{t+1}(v_t^i)|}(v^{i+1},v_t^i)\in E,\varphi (v^{i+1})=t+1\\ & 0(v^{i+1},v_t^i)\in E,\varphi (v^{i+1})\ne t+1\\ & 0(v^{i+1},v_t^i)\notin E\end{array}$$
3.Recursive guidance for random walkers,i.e.,由于metapath是对称的，所以有：
$$p(v^{i+1},v_t^i)=p(v^{i+1},v_l^i),\text{ if }t=l$$

细节三：softmax and negative sampling

softmax in metapath2vec
$$p(c_t|v;\theta )=\frac{e^{X_{c_t}\cdot X_v}}{{\sum }_{u\in V}{e}^{X_u\cdot X_v}}=\frac{e^{X_{c_t}}\cdot e^{X_v}}{{\sum }_{u\in V}{e}^{X_u}\cdot e^{X_v}}\text{\hspace{1em}(2)}$$
softmax in metapath2vec++
$$p(c_t|v;\theta )==\frac{e^{X_{c_t}}\cdot e^{X_v}}{{\sum }_{u_t\in V_t}{e}^{X_{u_t}}\cdot e^{X_v}}\text{\hspace{1em}(3)}$$
可以看到metapath2vec++在做softmax的时候不是针对所有节点V的，而是对某个类型$V_t$来做softmax。另外公式2中将所有项加起来和为1，公式3将所有项加起来，和不为1，如果节点有4个类型，那么和为4，每一个类型的和为1.
负采样公式上面有，不重复了

细节四 heterogeneous skip-gram node representation

论文的图2caption里面讲得很清楚了，就是按节点类型分别进行表征（红色框框）。注意看每个最后按节点类型进行表征的维度大小和该类型所含节点数量是一样的。

The heterogeneous skip-gram used in metapath2vec++. Instead of one set of multinomial distributions for all types of neighborhood nodes in the output layer, it specifies one set of multinomial distributions for each type of nodes in $a_4$’s neighborhood. $V_t$ denotes one specifies $t$-type nodes and $V=V_V\cup V_A\cup V_O\cup V_P$ . $k_t$ specifies the size of a particular type of one’s neighborhood and $k=k_V+k_A+k_O+k_P$.

实验结果及分析

数据集介绍

两个数据集：Aminer、DBIS，每个数据集中节点种类是3
例如：
Aminer:$|V_A|=9,323,739,|V_P|=3,194,405,|V_V|=3,883$
Baselines: DeepWalk，node2vec、LINE、PTE、Spectral Clustering、Graph Factorization
多个任务：节点分类（Multi-Class Classification）、节点聚类（Node Clustering）、相似性（Case Study:Similarity Search）、可视化（Case Study:Visualization）、参数实验（Scalability）

实验参数

(1) The number of walks per node w: 1000;
(2) The walk length l: 100;
(3) The vector dimension d: 128(LINE: 128 for each order);
(4) The neighborhood size k: 7;
(5) The size of negative samples: 5.
meta-path schemes in heterogeneous academic networks are APA and APVPA

Multi-label Classification 节点分类

论文先介绍了数据集中节点的分类label如何获得的。例如会议是通过Google Scholar来匹配：1. Computational Linguistics, 2. Computer Graphics, 3. Computer Networks &
Wireless Communication, 4. Computer Vision & Pattern Recognition, 5. Computing
Systems, 6. Databases & Information Systems, 7. Human Computer Interaction, and 8.
Theoretical Computer Science
venue node分类结果：

特别说明：在数据比较少的时候，算法结果比baseline效果要特 别 好（乐夏梗）。

Node clustering 节点聚类

用NMI来衡量，值越大越好。
聚类结果是在得到节点表征后运行k均值算法得到的。

Case Study: Similarity Search

取21 query nodes，然后用 cosine similarity计算相似度，得到查询结果。
从表中结果看到，自己和自己的相似度肯定最大，所以第一行
而且同档次的会议都排在一起，说明效果还不错。

论文总结

关键点
异质图的理解
meta-path的概念
损失函数的表达
skip-gram一组多项分布

创新点
基于meta-path的随机游走
softmax的修改
负采样的修改
异质图实验论证

启发点
对异质图的理解，多类型的点和边的定义
是异质图表征学习的早期代表性工作，高引用量
random walk +skip2gram的经典框架
算法的设计，将同质图经典框架通过修改损失函数、softmax和负采样，适用到异质图
属于新问题，从图的类型驱动开展的研究工作

代码复现