论文阅读笔记 Prototypical Networks for Few-shot Learning

小样本学习的原型网络

论文原文链接：https://arxiv.org/abs/1703.05175

摘要

作者提出了一种小样本分类问题的原型网络，在这种网络中，分类器必须推广到训练集中没有的新类别，每个新类别只有少量样例。该原型网络学习一个度量空间，通过计算每个类的原型表示的距离进行分类。与最近的小样本学习方法相比，该方法反映出更简单的归纳偏好，这有益于这种有限数据的状况，因此取得了出色的效果。作者给出的分析表明，某些简单的设计决定能够产生实质的改进，超过了最近的方法，包括复杂的架构选择和元学习。作者把该原型网络进一步扩展到零样本学习，在 CU-Birds 数据集上取得了最高水准的结果。

1 引言

在小样本分类[20,16,13]任务中，分类器必须适应训练中没见过的新类别，每个类别只有少量样例。朴素的方法，例如，在新数据上再次训练模型，会严重过拟合。虽然这个问题很难，但事实表明人类能够处理，即使是单样例分类，每个类别只有一个样例，也能达到很高的准确率[16]。

在小样本学习领域，最近有两种方法取得了重大进展。Vinyals 等人[29]提出的匹配网络（matching networks），首先在带标签的数据集（支持集）上学到特征向量，然后对该特征向量使用注意力机制来预测无标签数据（查询集）的类别。匹配网络可解释为，一个加权最近邻分类器应用于一个特征空间。尤其是，这个模型在训练期间利用采样得到的小批量样例（称为片段），设计的每个片段是用来模拟小样本任务，这种片段是通过对类别和样例进行二段抽样得到的。片段的使用使得模型训练对于测试环境来说更加准确可靠，因此提高了模型的泛化能力。Ravi 等人[22]进一步发展了片段训练的思想，提出了小样本学习的元学习方法，该方法会训练一个LSTM[9]来产生分类器的更新，给定一个片段，使得该片段很好地泛化到测试集（这句话不太理解）。这里，不是在多个片段上训练一个单独的模型，而是LSTM元学习器学习为每个片段训练一个量身定制的模型。

作者通过解决过拟合的关键问题，来解决小样本学习问题。由于数据非常有限，作者假设分类器应该具有非常简单的归纳偏好。作者提出的原型网络的核心思想是，存在一个特征空间，在该特征空间中，样例簇拥在每个类的单一原型表示周围。为了做到这一点，作者使用神经网络把所有原始数据转换到一个特征空间，然后把支持集样例特征向量的均值作为类别原型，只是通过寻找最近的类别原型来对查询样例进行分类。

作者采用同样的方法来解决零样本学习问题，在零样本学习中，没有带标签的样例，每个类别只有元数据给出的粗略描述。因此作者把这些元数据转换为特征向量，作为每个类别的原型。对查询样例的分类方法和小样本场景一样，都是寻找距离查询样例最近的类别原型。

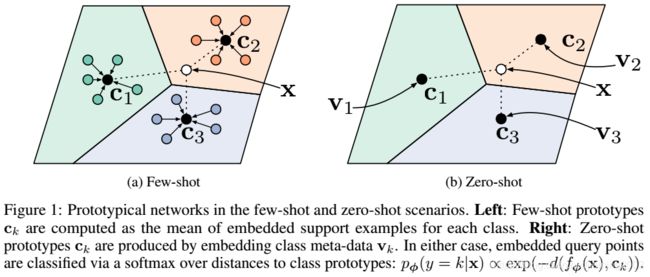
图1 小样本和零样本场景中的原型网络。左图：小样本原型是每个类别的支持样例的嵌入特征的均值。右图：零样本原型是每个类别的原数据的嵌入特征。不管在哪种情况下，对查询样例的分类方法都是相同的，即先计算查询样例的嵌入特征与每个类别原型的距离，然后取softmax值进行分类。

本文阐明了小样本学习的原型网络，以及零样本学习的原型网络。绘制了单样本学习中匹配网络的关系（这句话不太理解），分析了模型中使用的距离函数。特别地，当距离用布雷格曼散度（Bregman divergence）计算时，例如，平方欧式距离，为了证明使用类别均值作为原型更合理，作者把该原型网络与聚类联系起来。作者从经验上发现距离的选择至关重要，欧式距离远远好于更常用的余弦相似度。在一些基准任务上，达到了最高性能。原型网络比最近的元学习算法更简单、更有效，这使得原型网络成为吸引人的方法。

2 原型网络

2.1 符号定义

支持集 $S=\{(x_1,y_1),...,(x_n,y_n)|x_i\in R^D,y_i\in \{1,...,k\}\}$ 有 n 个样例，k 个类别，其中 $x_i$ 是样例的 D 维特征向量，$y_i$ 是对应的类别标签。

$S_k$ 表示类别 k 的带标签样例集。

2.2 模型

原型网络通过嵌入特征函数 $f_{\varphi }:R^D\to R^M$（$\varphi$ 是可学习的参数）为每个类计算一个 M 维的特征向量 $c_k\in R^M$ 称为原型。每个类的原型是该类别的支持样例的嵌入特征的均值。

$c_k=\frac{1}{|S_k|}{\sum }_{(x_i,y_i)\in S_k}{f}_{\varphi }(x_i)$ ---------- (1)

给定距离函数 $d:R^M\times R^M\to [0,+\infty )$，原型网络在嵌入特征空间中，基于查询样例 $x$ 到每个类别原型的距离的 softmax 值，生成 $x$ 的类别分布。

$p_{\varphi }(y=k|x)=\frac{exp(-d(f_{\varphi }(x),c_k))}{{\sum }_{k^{\prime }}exp(-d(f_{\varphi }(x),c_k))}$ ------------- (2) 其实就是 softmax 函数

模型训练是通过 SGD 最小化真实类别 k 的负log概率 $J(\varphi )=-log{p}_{\varphi }(y=k|x)$（个人理解：SGD 是让函数值最小化，log概率是单调递增函数，因此用负log概率，当函数值最小时，概率取最大值。查询样例属于真实类别 k 的概率）。训练片段的构造过程，首先从训练集中随机选择类别的子集，然后从这个子集的每个类别中选择样例的子集，最后把这些样例子集拆分为支持集和查询集。
算法1 是计算训练片段的损失 $J(\varphi )$ 的伪代码（更新loss的公式居然是，距离+距离的log，不太理解）。

2.3 作为混合密度估计的原型网络

对于一种特殊的距离函数，称为常规布雷格曼散度（regular Bregman divergences），原型网络算法等同于在支持集上使用指数族密度（exponential family density）进行混合密度估计。常规布雷格曼散度的计算公式为：

$d_{\phi }(z,z^{\prime })=\phi (z)-\phi (z^{\prime })-(z-z^{\prime }{)}^T\nabla \phi (z^{\prime })$ ---------- (3)

其中 $\phi$ 是一个勒让德式可微分的严格凸函数。布雷格曼散度的实例包括平方欧氏距离 $||z=z^{\prime }|{|}^2$ 和马氏距离（Mahalanobis distance）。

原型的计算可看作支持集上的硬聚类，每个类别被聚成一簇，而且每个样例被归入其对应的类簇。就布雷格曼散度而言，类簇的质心是簇的均值。因此使用布雷格曼散度时，对于给定的有标签支持集，等式(1)计算的原型能够得到类簇的最佳质心。

此外，任何常规指数族分布 $p_{\psi }(z|\theta )$ （θ是参数，ψ 是累积函数），可写为一个唯一确定的正则布雷格曼散度：

$p_{\psi }(z|\theta )=exp\{z^T\theta -\psi (\theta )-g_{\psi }(z)\}=exp\{-d_{\phi }(z,\mu (\theta ))-g_{\phi }(z)\}$ (4)

现在考虑一个参数为 $\Gamma =\{{\theta }_k,{\pi }_k{\}}_{k=1}^K$ 的常规指数族混合模型:

$p(z|\Gamma )={\sum }_{k=1}^K{\pi }_k{p}_{\psi }(z|{\theta }_k)={\sum }_{k=1}^K{\pi }_{k}exp(-d_{\phi }(z,\mu ({\theta }_k))-g_{\phi }(z))$ (5)

给定参数 $\Gamma$，对于一个无标签样例 z 所属的类簇，根据下式进行推断：

$p(y=k|z)=\frac{{\pi }_{k}exp(-d_{\phi }(z,\mu ({\theta }_k)))}{{\sum }_{k^{\prime }}{\pi }_{k^{\prime }}exp(-d_{\phi }(z,\mu ({\theta }_k)))}$ (6)

对于每个类一个簇的等权混合模型，簇的赋值推断等同于利用 $f_{\varphi }(x)=z$ 和 $c_k=\mu ({\theta }_k)$ 查询类别预测。在这种情况下，原型网络使用由 $d_{\phi }$ 确定的指数族分布，能有效地进行混合密度估计。因此，距离的选择指定了嵌入特征空间中类别条件数据分布建模的假设。

2.4 作为线性模型的重新解释

一个简单的分析有助于深入了解学到的分类器的本质。使用欧氏距离时，式(2)中的模型等同于一个具有特定参数的线性模型。要看清楚这一点，可以在指数中展开该项：

$-||f_{\varphi }(x)-c_k|{|}^2=-f_{\varphi }(x{)}^T{f}_{\varphi }(x)+2c_k^T{f}_{\varphi }(x)-c_k^T{c}_k$ (7)

对于给定的类别 k，式(7)中的第一项是常数，因此该项不影响 softmax 函数的输出结果。可以把式(7)中其余的项写为一个线性模型：

$2c_k^T{f}_{\varphi }(x)-c_k^T{c}_k=w_k^T{f}_{\varphi }(x)+b_k,其中w_k=2c_k,b_k=-c_k^T{c}_k$ (8)

本工作中，作者主要关注平方欧氏距离（对应于球面高斯密度）。尽管等价于线性模型，实验结果表明欧式距离很有效。作者假设这是因为所有需要学习的非线性因素都能在嵌入函数中学到。确实，这是现代神经网络分类系统正在使用的方法，例如[14][28]。

2.5 与匹配网络的比较

在小样本学习中，原型网络不同于匹配网络，而在单样例情景中，它们是等价的。匹配网络根据给定的支持集生成一个加权最近邻分类器，而原型网络使用平方欧式距离生成一个线性分类器。在单样例学习的情况下，由于每个类别只有一个支持样例，所以 $c_k=x_k$，此时匹配网络和原型网络是等价的。

一个自然的问题是每个类使用多个原型是否有意义，而不是只使用一个原型。如果每个类的原型数量是固定的并且大于1，那么这就需要一个分区方案来进一步对每个类别中的支持样例进行聚类。Mensink 等人[19]和 Rippel 等人[25]已经提出了这种方法，但是这两个方法都需要一个从权重更新模块解耦的独立的划分阶段，而作者的方法只是利用普通的梯度下降法进行学习。

Vinyals 等人[29]提出的一些扩展，包括解耦嵌入函数（作用于支持集和查询集的），以及使用第二级、全条件嵌入（FCE）考虑到每个片段中的具体样例（这句话不太理解）。这些扩展同样可以整合到原型网络中，但是会增加可学习的参数量，而且 FCE 要使用双向 LSTM 对支持集施加任意排序。相反，作者证明使用简单的设计选型可以实现相同的性能水平。

2.6 设计选型

距离度量 Vinyals 等人[29]和 Ravi 等人[22]在匹配网络中使用的是余弦距离。但是对于原型网络和匹配网络，任何距离都是允许的，而且作者发现，使用平方欧氏距离可以大大提高这两种网络的性能。作者推测这主要是因为余弦距离不是布雷格曼散度，因此不能实现2.3节讨论的混合密度估计。

片段组成 一种构建片段的直接方式（Vinyals 等人[29]和 Ravi 等人[22]使用的）是选择 Nc 个类，每个类选择 Ns 个支持样例，以便匹配测试时预期的情境。也就是说，如果我们希望在测试时执行 5-way 1-shot 分类，那么训练片段可以由5个类别（每个类别一个样例）组成，即 Nc = 5，Ns = 1。但是作者发现使用更高的 Nc（类别数量）进行训练，非常有益。作者的实验是在一个外置的验证集上调优 Nc。另一个要考虑的是，是否应该匹配训练和测试时的 Ns（样例数量）。对于原型网络，作者发现使用相同的 Ns 进行训练和测试，通常是最好的。

2.7 零样本学习

小样本学习是给定一个支持集用于训练，零样本学习与小样本学习不同，是给定每个类别的元数据向量 $V_k$。这些元数据向量可以事先确定，或者可以从原始文本中学习[7]。修改原型网络来处理零样本情况是很简单的，只需定义 $c_k=g_v(V_k)$ 作为元数据向量的一个单独的嵌入。图1显示了与小样本学习过程相关的原型网络的零样本学习过程。由于元数据向量和查询样例来自不同的输入域，作者根据经验发现，将原型的嵌入特征 g 设置为固定单位长度是有帮助的，但是没有限制查询样例的嵌入特征 f。

3 实验

小样本学习，使用数据集 Omniglot[16] 和 miniImageNet[26]，采用 Ravi 等人[22]的划分方法。

零样本学习，使用 2011 版的 Caltech UCSD bird 数据集(CUB-200 2011) [31]。

3.1 Omniglot 小样本分类

Omniglot 数据集是从 50 个字母表中收集到的 1623 个手写字符。每个字符有 20 个样例，每个样例是由不同的人手写的。作者采用 Vinyals 等人[29]的处理过程，把灰度图片缩放为 $28\times 28$，以90度的倍数旋转增加字符类。1200 个字符加上旋转（共4800个类别）用于训练，其余的字符（包括旋转）用于测试。嵌入模块采用 Vinyals 等人[29]的架构，由 4 个卷积块组成。每个卷积块有一个 64-filter 3 × 3 卷积层、批量归一层（batch normalization）、ReLU、 2 × 2 最大池化层。该架构输出的是 64 维的特征向量。使用同样的嵌入编码器来处理支持集和查询样例。所有的模型训练都是用带有 Adam[11] 的 SGD。初始学习率是 $10^{-3}$，每训练 2000 个片段将学习率降低一半。除了批量归一化，没有使用正则化。
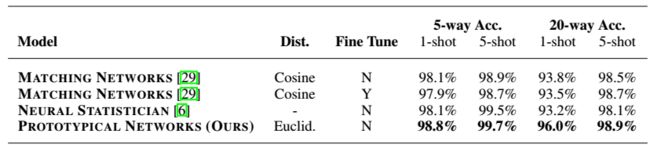
表1 Omniglot 数据集上的小样本分类准确率

3.2 miniImageNet 小样本分类

为了直接与最先进的小样本学习方法进行比较，采用 Ravi 等人[22]介绍的训练-测试集划分方法：把 100 个类别划分为不同的子集，64 训练集，16 验证集，20 测试集。

嵌入模块的架构和 Omniglot 实验中的相同，由于输入图片的尺寸增大了，输出的是 1600 维的特征向量。使用 Omniglot 实验中同样的学习率。使用 30-way 的片段训练 1-shot 分类，使用 20-way 的片段训练 5-shot 分类。测试 shot 数与训练相同，每个类包含 15 个查询样例。

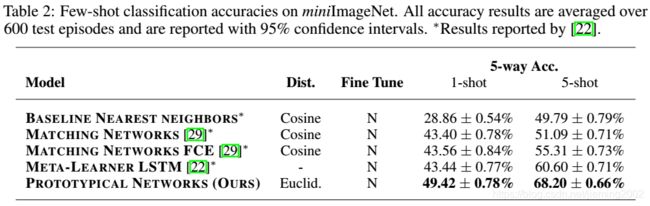
表2 miniImageNet 上的小样本分类准确率。所有的准确率是 600 个测试片段的平均值，95%的置信区间。

作者对不同的距离度量和每个片段的训练类别数量，在原型网络和匹配网络上的性能，进行了进一步的分析。

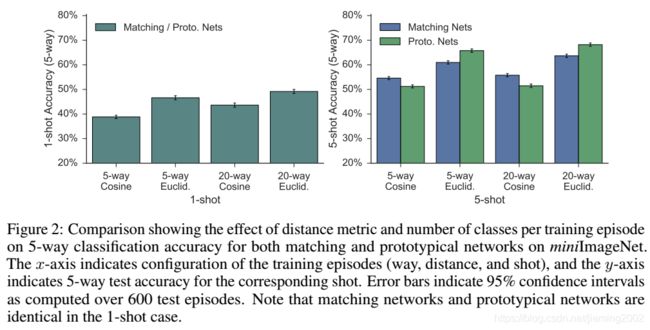
图2 实验结果

3.3 CUB 零样本分类

为了评估本文的方法在零样本学习中的适用性，作者在 2011 版的 Caltech UCSD bird 数据集(CUB-200 2011) [31]上进行了实验。严格按照 Reed 等人[23]的方法来准备数据。使用 GoogLeNet 修剪图像（中央、左上角、右上角、左下角、右下角）、水平翻转图像、提取图像特征，得到 1024 维的特征向量，用于训练。测试时，只对原图像进行中央修剪。对于类别的元数据，使用由 CUB 数据集提供的 312 维连续属性向量。这些属性编码了鸟类的各种特征，如它们的颜色、身材和羽毛图案。

在 1024 维图像特征和 312 维属性向量之上，学习了一个简单的线性映射，得到一个 1024 维输出空间。因为类别的属性向量和图像样例来自不同的域，对于该数据集，作者发现，对类原型（嵌入属性向量）进行规范化很有用。每个训练片段有 50 个类别，每个类别有 10 个查询样例。使用带有 Adam 的 SGD 对嵌入特征进行优化，学习率固定为 $10^{-4}$ 权重衰减为 $10^{-5}$。采用早期停止法（根据验证损失）来确定再训练的（在训练加验证集上）最佳周期数。

表3 CUB-200 上的零样本分类准确率

4 相关工作

关于度量学习的文献很多。本文的方法与 NCA[27] 的非线性扩展最为相似。本文的方法也类似于最近类别均值法[19]。

5 结论

作者提出了一种小样本学习的简单的原型网络方法，其思想是可以在神经网络学到的表示空间中，通过每个类别的样例特征的均值来表示该类别。

【本期作者主页】https://blog.csdn.net/jieming2002