方向梯度直方图（HOG）

引言

向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。Hog特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。需要提醒的是，HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的，而如今虽然有很多行人检测算法不断提出，但基本都是以HOG+SVM的思路为主。

主要思想

一副图像中，局部目标表观和形状（appearance and shape）能够被梯度或边缘的方向密度分布很好地描述。（其本质在于：梯度的统计信息，而梯度主要存在于边缘的地方，就类似于LBP编码的统计信息，大家都是用直方图来表示）。首先将图像分成小的连通区域，通常称细胞单元（cell）。然后采集胞元中各像素点的梯度的或边缘的方向直方图，最后把这些直方图组合起来就可以构成一种特征描述了。

block

把这些局部直方图在图像的更大的范围内（我们把它叫区间或block）进行对比度归一化（contrast-normalized），所采用的方法是：先计算各直方图在这个区间（block）中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后，能对光照变化和阴影获得更好的效果。

与其他的特征描述方法相比，HOG有很多优点。首先，由于HOG是在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。其次，在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。

HOG特征提取

对检测窗口进行如下操作：

1）颜色空间归一化

由于图像的采集环境、装置等因素，采集到的图像效果可能不是很好，容易出现误检或漏检的情况，所以需要对采集到的人脸进行图像预处理，主要是处理光线太暗或太强的情况，这里有两次处理：图像灰度化、Gamma校正。

1、灰度处理
对于彩色图像，将RGB分量转化成灰度图像，其转化公式为：

Gray=0.3×R+0.59×G+0.11×B

2、gamma校正

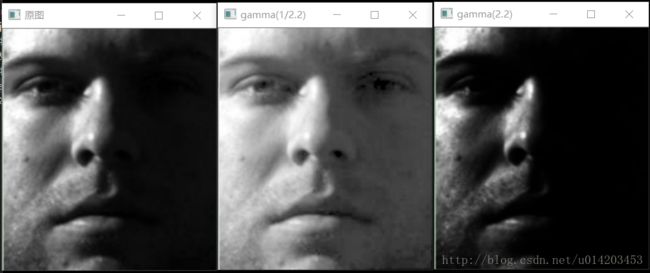
在实际情况下，图像经常会出现照度不均匀、局部阴影等情况，为了达到较好的检测效果，检测器需要对光照不敏感。这里一般使用Gamma校正法对输入图像进行颜色空间的标准化（归一化），从而将图像整体亮度提高或降低，调节图像的对比度，减少图像局部的阴影和光照变化带来的影响，提高算法对光照的鲁棒性。

关于gamma矫正

在实际中可以采用两种不同的方式进行Gamma标准化，平方根、对数法。这里我们采用平方根的办法，公式如下（其中γ=0.5、1/2.2）：

f(I)=Iγ

为什么使用gamma矫正？

这里不得不提到韦伯定律，那么，什么是韦伯定律呢？其定义为感觉的差别阈限随原来刺激量的变化而变化，且表现为一定的规律性，即

△Φ/Φ=C

其中Φ为原刺激量，△Φ为此时的差别阈限，C为常数，又称为韦伯率。简而言之，就是人对自然界刺激的感知，是非线性的，外界以一定的比例加强刺激，对人来说，这个刺激是均匀增长的。（也就是自然界的一个物理量是非线性变化的，这对于人来说可能是线性的，人通过比较来感知世界），比如：里氏地震级数，每增加一级，释放的物理能量大32倍；声音的强度是按照“分贝”来描述，倍数增加的音量听起来是均匀增加的。其中值得注意一点是，人眼是按照γ < 1的曲线对输入图像进行处理的。

使用须知

作者在他的博士论文里有提到，对于涉及大量的类内颜色变化，如猫，狗和马等动物，没标准化的RGB图效果更好，而牛，羊的图做gamma颜色校正后效果更好。gamma校正需要适应你的数据，你需要分析你的数据特性，需不需要把图像变亮\暗一点。

int main()  
{  
    Mat picture = imread("test.jpg", 0);//灰度  
    Mat img;  
    picture.convertTo(img, CV_32F); //转换成浮点  
    sqrt(img, img);                 //gamma校正  
    normalize(img, img, 0, 255, NORM_MINMAX, CV_8UC1);//归一化像素值[0,255]  
    imshow("原图", picture);  
    imshow("Gamma校正", img);  
    waitKey();  

    return 0;  
}

2）每个像素点的梯度计算（大小、方向）

主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。对经过颜色空间归一化后的图像，求取其梯度及梯度方向。分别在水平和垂直方向进行计算，水平梯度算子：[−1 0 1]，垂直梯度算子：[−1 0 1]T。

Gx(x,y)=I(x+1,y)−I(x−1,y)Gy(x,y)=I(x,y+1)−I(x,y−1)G(x,y)=G2x(x,y)+G2y(x,y)−−−−−−−−−−−−−−−√θ(x,y)=arctan(Gy(x,y)Gx(x,y))

代码如下：

#include   
#include   
#include   
#include   
#include   

using namespace cv;  
using namespace std;  

int main()  
{  
    Mat picture = imread("test.jpg", 0);//灰度  
    Mat img;  

    picture.convertTo(img, CV_32F); //转换成浮点  
    sqrt(img, img);                 //gamma校正  
    normalize(img, img, 0, 255, NORM_MINMAX, CV_32F);//归一化[0,255]浮点数  

    Mat gradient = Mat::zeros(img.rows, img.cols, CV_32F);//梯度  
    Mat theta = Mat::zeros(img.rows, img.cols, CV_32F);//角度  

    for (int i = 1; i < img.rows - 1; i++)  
    {  
        for (int j = 1; j < img.cols - 1; j++)  
        {  
            float Gx, Gy;  

            Gx = img.at<float>(i, j + 1) - img.at<float>(i, j - 1);  
            Gy = img.at<float>(i + 1, j) - img.at<float>(i - 1, j);  

            gradient.at<float>(i, j) = sqrt(Gx * Gx + Gy * Gy);//梯度模值  
            theta.at<float>(i, j) = float(atan2(Gy, Gx) * 180 / CV_PI);//梯度方向[-180°，180°]  
        }  
    }  

    normalize(gradient, gradient, 0, 255, NORM_MINMAX, CV_8UC1);//归一化[0,255] 无符号整型  
    normalize(img, img, 0, 255, NORM_MINMAX, CV_8UC1);  

    imshow("原图", picture);  
    imshow("Gamma校正", img);  
    imshow("梯度图", gradient);  
    waitKey();  

    return 0;  
}  

好了，现在一个检测窗口中每个像素的梯度方向和幅值我们拿到，接下来是怎么将这些梯度用于表征检测窗口的问题，借鉴下前面的LBP特征表达，很显然最简单的方法就是统计下梯度信息（方向、大小）。和前面的LBP一样，他也是在一个领域内统计梯度信息，这个领域可以是矩形、圆形或星型，但实践证明矩形效果比较好点，不过这里的这个矩形领域我们一般把他称为胞元（cell）。

3）梯度信息统计

1）将图像化成小的胞元，统计每个cell的梯度直方图

将图像分成若干个胞元（如8X8），假设采用9个bin的直方图来统计这8∗8个像素的梯度信息，即将cell的梯度方向0～180度（或0～360度，考虑了正负，signed）分成9个方向块。如下图所示：如果这个像素的梯度方向是20-40度，直方图第2个bin即的计数就加1，这样，对cell内每个像素用梯度方向在直方图中进行加权投影，将其映射到对应的角度范围块内，就可以得到这个cell的梯度方向直方图了，就是该cell对应的9维特征向量（因为有9个bin）。这边的加权投影所用的权值为当前点的梯度幅值。也就是说某个像素的梯度方向是30°，其梯度幅值是4，那么直方图第2个bin的计数就不是加1了，而是加4。这样就得到关于梯度方向的一个加权直方图。

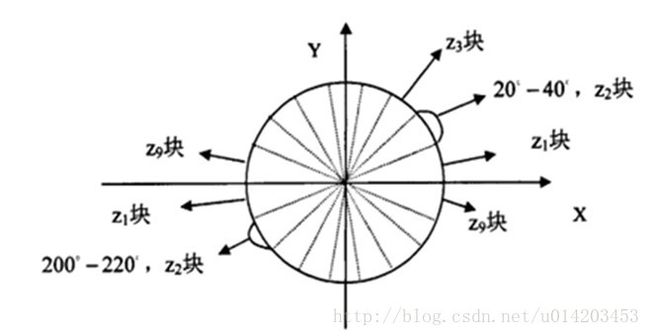
根据Dalal等人的实验，在行人目标检测中，在无符号方向角度范围并将其平均分成9份（bins）能取得最好的效果，当bin的数目继续增大效果改变不明显，故一般在人体目标检测中使用bin数目为9范围0~180度的度量方式。

2）归一化与块描述

由于局部光照的变化以及前景-背景对比度的变化，使得梯度强度的变化范围非常大。归一化能够进一步地对光照、阴影和边缘进行压缩，使特征向量空间对光照，阴影和边缘变化具有鲁棒性。一般的做法是：把各个胞元组合成大的、空间上连通的区域（blocks）。这样，一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的，这就意味着：每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。

Dalal采用了四种不同的方法对区间进行归一化，并对结果进行了比较。引入 v表示一个还没有被归一化的向量，它包含了给定区间（block）的所有直方图信息。||v||k表示 v 的 k 阶范数，这里的 k={1,2}。用 ϵ 表示一个很小的常数。这时，归一化因子可以表示如下：

• L2 norm：f=v||v||22+ϵ2√
• L2−hys：上述归一化的省略式，操作中先做一次L2 norm，再把>=0.2的分量赋值为0.2后再做一次L2 norm。
• L1 norm：f=v||v||1+ϵ2
• L1−sprt：f=v||v||1+ϵ2−−−−−−√

作者发现：采用L2-Hys, L2-norm, 和 L1-sqrt方式所取得的效果是一样的，L1-norm稍微表现出一点点不可靠性。但是对于没有被归一化的数据来说，这四种方法都表现出来显著的改进。

如何加快梯度直方图统计？（三线性插值）

在计算每个cell的梯度直方图时，可以用三线性插值来提高计算速率。对于每个cell里的点，我们认为它是一个三维向量(x,y,θ)，如下图所示某一待处理像素点它位于block中的C0单元中， 利用该点与四个cell中的中心像素点 （图中4个圆点，(x1,y1),…,(x4,y4)） 的距离计算权值， 将待处理像素点的梯度幅值分别加权累加到C0、C1、 C2、 C3中相应的直方图上，与θ相邻的两个bin上（θ1，θ2），其关键在于以何种方式将待处理点的梯度分配至4个胞元。

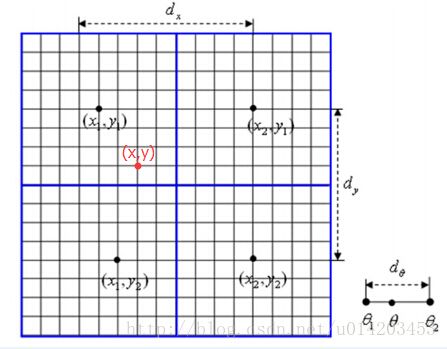
关于三线性插值的解释具体可以先参考 博客。根据上图，以 (x,y,θ) 对cell0的梯度直方图即h(x1,y1,θ1)的加权投影为例，三线性插值公式如下：

h(x1,y1,θ1)+=G(x,y)(1−x−x1dx)(1−y−y1dy)(1−θ(x,y)−θ1dθ)h(x1,y1,θ2)+=G(x,y)(1−x−x1dx)(1−y−y1dy)(θ(x,y)−θ1dθ)

其他3个点的梯度也依此方式更新，最终就得到4个cell的梯度直方图。

4）最终的HOG特征

将图像image内的所有block的HOG特征串联起来就可以得到该image（你要检测的目标）的HOG特征描述了。以OpenCV的HOG特征生成为例，有如下参数：

胞元cell大小：每个胞元特征：区间bolock：检测窗口：块滑动步长：8×89维2×2 cell64×128x,y方向均是8像素

每个block的特征维度为： 9×4=36
每次滑动8像素可以产生多少block?按卷积的公式来计算

(64−88+1)×(128−88+1)=7×15=105块

整个检测窗口的特征维度： 36×105=3780

到此，就可以将该特征向量扔给分类器进行分类了，Enjoy it！

HOG特征算法
HOG特征可视化
PHOG