入门XGBoost

欢迎访问我的技术博客：SnailDove ，本文内容有大量公式，csdn对数学公式支持不好，请访问本文原链接：一起入门xgboost

前言

在深度学习火起来之前，集成学习 （ensemble learning 包括 boosting: GBDT, XGBoost）是 kaggle 等比赛中的利器，所以集成学习是机器学习必备的知识点，如果提升树或者GBDT不熟悉，最好先看一下我的另一文： 《统计学习方法》第8章 提升方法之AdaBoost\BoostingTree\GBDT ，陈天奇 的 XGBoost (eXtreme Gradient Boosting) 和 微软的 lightGBM 是 GBDT 算法模型的实现，非常巧妙，是比赛的屠龙之器，算法不仅仅是数学，还涉及系统设计和工程优化。以下引用陈天奇 XGBoost论文 的一段话：

Among the 29 challenge winning solutions 3 published at Kaggle’s blog during 2015, 17 solutions used XGBoost. Among these solutions, eight solely used XGBoost to train the model, while most others combined XGBoost with neural nets in ensembles. For comparison, the second most popular method, deep neural nets, was used in 11 solutions. The success of the system was also witnessed in KDDCup 2015, where XGBoost was used by every winning team in the top-10. Moreover, the winning teams reported that ensemble methods outperform a well-configured XGBoost by only a small amount [1].

正文

XGBoost

快速了解

这部分内容基本上是对陈天奇幻灯片：官网幻灯片

outlook 幻灯片大纲

• 监督学习的主要概念的回顾
• 回归树和集成模型 (What are we Learning)
• 梯度提升 (How do we Learn)
• 总结

Review of key concepts of supervised learning 监督学习的关键概念的回顾

概念

符号	含义
$R^d$	特征维度为d的数据集
$x_i\in R^d$	第i个样本
$w_j$	第j个特征的权重
${\hat{y}}_i$	$x_i$ 的预测值
$y_i$	第i个训练集的对应的标签
$\Theta$	特征权重的集合，$\Theta={w_j

模型

基本上相关的所有模型都是在下面这个线性式子上发展起来的
$${\hat{y}}_i=\sum _{j=0}^d{w}_j{x}_{ij}$$
上式中 $x_0=1$，就是引入了一个偏差量，或者说加入了一个常数项。由该式子可以得到一些模型：

• 线性模型，最后的得分就是 ${\hat{y}}_i$ 。

• logistic模型，最后的得分是sigmoid函数 $\frac{1}{1+e^{-{\hat{y}}_i}}$ 。然后设置阀值，转为正负实例。

• 其余的大部分也是基于 ${\hat{y}}_i$ 做了一些运算得到最后的分数

参数

参数就是 $\Theta$ ，这也正是我们所需要通过训练得出的。

训练时的目标函数

训练时通用的目标函数如下：
$$Obj(\Theta )=L(\Theta )+\Omega (\Theta )$$
在上式中 $L(\Theta )$ 代表的是训练误差，表示该模型对于训练集的匹配程度。$\Omega (\Theta )$ 代表的是正则项，表明的是模型的复杂度。

训练误差可以用 $L={\sum }_{i=1}^{n}l(y_i,{\hat{y}}_i)$ 来表示，一般有方差和logistic误差。

• 方差: $l(y_i,{\hat{y}}_i)=(y_i-{\hat{y}}_i{)}^2$
• logstic误差: $l(y_i,{\hat{y}}_i)=y_{i}ln(1+e^{-{\hat{y}}_i})+(1-y_i)ln(1+e^{{\hat{y}}_i})$

正则项按照Andrew NG的话来说，就是避免过拟合的。为什么能起到这个作用呢？正是因为它反应的是模型复杂度。模型复杂度，也就是我们的假设的复杂度，按照奥卡姆剃刀的原则，假设越简单越好。所以我们需要这一项来控制。

• L2 范数: $\Omega (w)=\lambda ||w|{|}_2$
• L1 范数(lasso): $\Omega (w)=\lambda ||w|{|}_1$

常见的优化函数有有岭回归，logstic回归和Lasso，具体的式子如下​

• 岭回归，这是最常见的一种，由线性模型，方差和L2范数构成。具体式子为 $\sum _{i=1}^n(y_i-w^T{x}_i)2+\lambda ||w|{|}_2$

• logstic回归，这也是常见的一种，主要是用于二分类问题，比如爱还是不爱之类的。由线性模型，logistic 误差和L2范数构成。具体式子为 $\sum _{i=1}^n[y_{i}ln(1+e^{-w^T{x}_i})+(1-y_i)ln(1+e^{w^T{x}_i})]+\lambda ||w|{|}_2$

• lasso比较少见，它是由线性模型，方差和L1范数构成的。具体式子为 $\sum _{i=1}^n(y_i-w^T{x}_i{)}^2+\lambda ||w|{|}_1$

我们的目标的就是让 $Obj(\Theta )$ 最小。那么由上述分析可见，这时必须让 $L(\Theta$ ) 和 $\Omega (\Theta )$ 都比较小。而我们训练模型的时候，要在 bias 和 variance 中间找平衡点。bias 由 $L(\Theta )$ 控制，variance 由 $\Omega (\Theta )$ 控制。欠拟合，那么 $L(\Theta )$ 和 $\Omega (\Theta )$ 都会比较大，过拟合的话 $\Omega (\Theta )$ 会比较大，因为模型的扩展性不强，或者说稳定性不好。

回归树和集成模型 (What are we Learning)

Regression Tree (CART)

回归树，也叫做分类与回归树，我认为就是一个叶子节点具有权重的二叉决策树。它具有以下两点特征

• 决策规则与决策树的一样。

• 每个叶子节点上都包含了一个权重，也有人叫做分数。

  下图就是一个回归树的示例：

回归树的集成模型

回归

小男孩落在第一棵树的最左叶子和第二棵树的最左叶子，所以它的得分就是这两片叶子的权重之和，其余也同理。

树有以下四个优点：

1. 使用范围广，像GBM，随机森林等。(PS:据陈天奇大神的统计，至少有超过半数的竞赛优胜者的解决方案都是用回归树的变种)
2. 对于输入范围不敏感。所以并不需要对输入归一化
3. 能学习特征之间更高级别的相互关系
4. 很容易对其扩展

模型和参数

假设我们有 $K$ 棵树，那么
KaTeX parse error: Expected 'EOF', got '\cal' at position 49: …i),\ \ f_k \in \̲c̲a̲l̲ ̲F
上式中 KaTeX parse error: Expected 'EOF', got '\cal' at position 1: \̲c̲a̲l̲ ̲F 表示的是回归森林中的所有函数空间。$f_k(x_i)$ 表示的就是第 $i$ 个样本在第 $k$ 棵树中落在的叶子的权重。那么现在我们需要求的参数就是每棵树的结构和每片叶子的权重，或者简单的来说就是求 $f_k$ 。那么为了和上一节所说的通用结构统一，可以设
$$\Theta =\{f_1,f_2,f_3,\cdots ,f_k\}$$

在单一变量上学习一棵树

• 定义一个目标对象，优化它。
• 例如：
  • 考虑这样一个问题：在输入只有时间（t）的回归树
  • 我想预测在时间是t的时候，我是否喜欢浪漫风格的音乐？

可见分段函数的分割点就是回归树的非叶子节点，分段函数每一段的高度就是回归树叶子的权重。那么就可以直观地看到欠拟合和过拟合曲线所对应的回归树的结构。根据我们上一节的讨论，$\Omega (f)$ 表示模型复杂度，那么在这里就对应着分段函数的琐碎程度。$L(f)$ 表示的就是函数曲线和训练集的匹配程度。

学习阶跃函数

第二幅图：太多的分割点，$\Omega (f)$ 即模型复杂度很高；第三幅图：错误的分割点，$L(f)$ 即损失函数很高。第四幅图：在模型复杂度和损失函数之间取得很好的平衡。

综上所述

模型：假设我们有k棵树，那么模型的表达式 KaTeX parse error: Expected 'EOF', got '\cal' at position 51: …k(x_i), f_k\in \̲c̲a̲l̲{F}

目标函数：$Obj=\underset{训练误差}{\sum _{i=1}^{n}l(y_i,\widehat{y_i})}+\underset{树的复杂度}{\sum _{k=1}^K\Omega (f_k)}$

定义树的复杂度几种方式

• 树的节点数或深度
• 树叶子节点的L2范式
• …（后面会介绍有更多的细节）

目标函数 vs 启发式

当你讨论决策树，它通常是启发式的

• 按信息增益
• 对树剪枝
• 最大深度
• 对叶子节点进行平滑

大多数启发式可以很好地映射到目标函数

• 信息增益 -> 训练误差
• 剪枝 -> 按照树节点的数目定义的正则化项
• 最大深度 -> 限制函数空间
• 对叶子值进行平滑操作 -> 叶子权重的L2正则化项

回归树不仅仅用于回归

1. 回归树的集成模型定义了你如何创建预测的分数，它能够用于

   • 分类，回归，排序 …
   • …

2. 回归树的功能取决于你怎么定义目标函数

3. 目前为止我们已经学习过

   • 使用方差损失（Square Loss） $l(y_i,\widehat{y_i})=(y_i-{\hat{y}}_i)$ ，这样就产生了普通的梯度提升机（common gradient boosted machine）
   • 使用逻辑损失（Logistic loss）$l(y,{\hat{y}}_i)=y_i\ln (1+e^{-{\hat{y}}_i})+(1-y_i)\ln (1+e^{{\hat{y}}_i})$ ，这样就产生了逻辑梯度提升（LogitBoost）。

梯度提升Gradient Boosting (How do we Learn)

那怎么学习？

• 目标对象：KaTeX parse error: Expected 'EOF', got '\cal' at position 62: …(f_k), f_k \in \̲c̲a̲l̲{F}
• 我们不能用像SGD（随机梯度下降）这样的方法去找到 f，因为他们是树而不是仅仅是数值向量。
• 解决方案：加法训练 Additive Training（提升方法boosting）
  • 从常量方法开始，每一次（轮）添加一个新的方法

这个算法的思想很简单，一棵树一棵树地往上加，一直到 $K$ 棵树停止。过程可以用下式表达：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \hat y_i^{(0)}…

加法训练

• 我们如何决定什么样的 $f$ 加到模型中？

  • 优化目标

• 在 $t$ 轮的预测是：$\hat y_i^{(t)} = \hat y_i^{(t - 1)} + f_t(x_i) $ 加号右边这一项就是我们在 t 轮需要决定的东西

  KaTeX parse error: No such environment: align at position 10: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &= \…

• 考虑平方误差
  KaTeX parse error: No such environment: align at position 10: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &=…
  $({\hat{y}}_i^{(t-1)}-y_i)$ 称为残差。

损失函数的泰勒展开

可由泰勒公式得到下式
$$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\Delta x+\frac{1}{2}{f}^{\prime \prime }(x)\Delta x^2$$
那么现在可以把 $y_i^{(t)}$看成上式中的 $f(x+\Delta x)$ ，$y_i^{(t-1)}$ 就是 $f(x)$ ，$f_t(x_i)$ 为 $\Delta x$ 。然后设 $g_i$ 代表 $f\prime (x)$ ，也就是 $g_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)})$ 用 $h_i$ 代表 $f\prime \prime (x)$， 于是 $h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}^{(t-1)})$ 于是现在目标函数就为下式:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &\ap…
可以用平方误差的例子进行泰勒展开看看结果是否一致，很明显，上式中后面那项 $[{\sum }_{i=1}^{n}l(y_i,{\hat{y}}_i^{(t-1)})+constant]$ 对于该目标函数我们求最优值点的时候并无影响，所以，现在有了新的优化目标
$$Ob{j}^{(t)}\approx \sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)$$

这么苦逼图啥？

改进树的定义 Refine the definition of tree

上一节讨论了 $f_t(x)$ 的物理意义，现在我们对其进行数学公式化。设 $w\in R^T$ ， $w$ 为树叶的权重序列，$q:R^d\to \{1,2,\cdots ,T\}$ ，q为树的结构。那么 q(x) 表示的就是样本 x 所落在树叶的位置。可以用下图形象地表示

现在对训练误差部分的定义已经完成。那么对模型的复杂度应该怎么定义呢？

定义树的复杂度 Define Complexity of a Tree

树的深度？最小叶子权重？叶子个数？叶子权重的平滑程度？等等有许多选项都可以描述该模型的复杂度。为了方便，现在用叶子的个数和叶子权重的平滑程度来描述模型的复杂度。可以得到下式：
$$\Omega (f_t)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
说明：上式中前一项用叶子的个数乘以一个收缩系数，后一项用L2范数来表示叶子权重的平滑程度。

下图就是计算复杂度的一个示例：

修改目标函数 Revisit the Objectives

最后再增加一个定义，用 $I_j$ 来表示第 $j$ 个叶子里的样本集合。也就是上图中，第 $j$ 个圈，就用 $I_j$ 来表示。
$$I_j=\{i|q(x_i)=j\}$$
好了，最后把优化函数重新按照每个叶子组合,并舍弃常数项：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &\ap…

这是 $T$ 个独立的二次函数的和。

结构分 The Structure Score

初中时所学的二次函数的最小值可以推广到矩阵函数里
$$\begin{gathered} \underset{x}{\min }\{Gx+\frac{1}{2}H{x}^2\}=-\frac{1}{2}\frac{G^2}{H},H>0 \\ \arg \underset{x}{\min }\{Gx+\frac{1}{2}H{x}^2\}=-\frac{G}{H}，H\ge 0 \end{gathered}$$
设 $G_j={\sum }_{i\in I_j}{g}_i,H_j={\sum }_{i\in I_j}{h}_i$ ，那么
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &= \…
因此，若假设我们的树的结构已经固定，就是 $q(x)$ 已经固定，那么
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ W_j^* &= - \fr…
例子

用于单棵树的搜索算法 Searching Algorithm for Single Tree

现在只要知道树的结构，就能得到一个该结构下的最好分数。可是树的结构应该怎么确定呢？

• 枚举可能的树结构 q

• 使用分数公式来计算 q 的结构分：

  $Obj=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$

• 找到最好的树结构，然后使用优化的叶子权重：

  $w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$

• 但是这可能有无限多个可能的树结构

树的贪婪学习 Greedy Learning of the Tree

• 从深度为 0 的树开始

• 对树的每个叶子节点，试着添加一个分裂点。添加这个分裂点后目标函数的值变化
  KaTeX parse error: No such environment: align at position 10: \begin{̲a̲l̲i̲g̲n̲}̲ Obj_{spl…

• 剩下的问题：我们如何找到最好的分裂点？

最好分裂点的查找 Efficient Finding of the Best Split

• 当分裂规则是 $x_j<a$ 时，树的增益是 ? 假设 $x_j$ 是年龄

• 我们所需要就是上图的两边 $g$ 和 $h$ 的和，然后计算
  $$Gain=\frac{G_L^2}{H_L+\lambda }+\frac{G_L^2}{H_L+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }-\gamma$$

• 在一个特征上，从左至右对已经排序的实例进行线性扫描能够决定哪个是最好的分裂点。

分裂点查找算法 An Algorithm for Split Finding

• 对于每个节点，枚举所有的特征
  • 对于每个特征，根据特征值对实例（样本）进行排序
  • 在这个特征上，使用线性扫描决定哪个是最好的分裂点
  • 在所有特征上采用最好分裂点的方案
• 深度为 $K$ 的生长树的时间复杂度
  • $O(Kdn\log n)$ ：每一层需要 $O(n\log n)$ 时间去排序，且需要在 $d$ 个特征上排序，我们需要在 $K$ 层进行这些排序。（补充：$O(n)$ 时间计算当前特征的最佳分裂点，即最后实际上 $O(dK(n\log n+n)$）
  • 这些可以进一步优化（例如：使用近似算法和缓存已经排序的特征）
  • 能够拓展到非常大的数据集

类变量（categorical variables）？

• 有一些树处理分开处理类变量和连续值的变量

  • xgboost可以简单地使用之前推导的分数公式去计算基于类变量的分裂分数

• 实际上，没有必要分开处理类变量

  • 我们可以使用独热编码（one-hot encoding）将类变量编码成数值向量。分配一个维度为类数量的向量。
    KaTeX parse error: Expected 'EOF', got '\cases' at position 8: z_j=\̲c̲a̲s̲e̲s̲{1,\quad &\text…

  • 如果有很多类变量，这个数值向量将是稀疏的，xgboost学习算法被设计成偏爱处理稀疏数据。

• 补充：对某个节点的分割时，是需要按某特征的值排序，那么对于无序的类别变量，就需要进行one-hot化。否则，举个例子：假设某特征有1，2，3三种变量，进行比较时，就会只比较左子树为1, 2或者右子树为2, 3，或者不分割，哪个更好，但是左子树为 1,3 的分割的这种情况就会忘记考虑。因为 $Gain$ 于特征的值范围是无关的，它采用的是已经生成的树的结构与权重来计算的。所以不需要对特征进行归一化处理。

剪枝和正则化 Pruning and Regularization

• 回忆一下增益公式：

  • $Gain=\underset{训练损失的减少量}{\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }}-\underset{正则项}{\gamma }$

  • 当训练损失减少量小于正则项的时候，分裂后的增益就变成负的。

  • 在树的简化度（simplicity）和预测性能（predictiveness）的权衡（trade-off）

• 提早终止（Pre-stopping）

  • 如果最好的分裂产生的增益计算出来是负的，那么停止分裂。
  • 但是（当前的）一个分裂可能对未来的分裂有益。

• 后剪枝 （Post-Prunning）

  • 生长一棵树到最大深度，再递归地剪枝所有具有负增益的叶子分裂节点。

回顾提升树算法 Recap: Boosted Tree Algorithm

• 每一轮添加一棵树

• 每一轮开始的时候，计算 $g_i={\partial }_{{\hat{y}}_i^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)}),h_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)})$

• 使用统计学知识（统计所有分裂点信息：一节梯度和二阶梯度），用贪婪的方式生长一棵树 $f_t(x)$ ：
  $$Obj=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

• 添加 $f_t(x)$ 到模型 ${\hat{y}}_i^{(t)}={\hat{y}}_i^{(t-1)}+f_t(x_i)$

  • 通常，我们这么做令 ${\hat{y}}_i^{(t)}={\hat{y}}_i^{(t-1)}+ϵf_t(x_i)$
  • $ϵ$ 称为步伐大小（step-size）或者收缩（shrinkage），通常设置为大约 0.1
  • 这意味着在每一步我们做完全优化，是为了给未来的轮次保留机会（去进一步优化），这样做有助于防止过拟合。

--------------------------------------------------------------幻灯片内容结束----------------------------------------------------------------------

XGBoost 系统设计

这部分内容主要来自陈天奇的论文 XGBoost: A Scalable Tree Boosting System

缩小和列抽样 shrinkage and column subsampling

随机森林中的用法和目的一样，用来防止过拟合，主要参考论文2.3节

• 这个xgboost与现代的gbdt一样，都有shrinkage参数 （最原始的gbdt没有这个参数）类似于梯度下降算法中的学习速率，在每一步tree boosting之后增加了一个参数 $\eta$（被加入树的权重），通过这种方式来减小每棵树的影响力，给后面的树提供空间去优化模型。
• column subsampling 列（特征）抽样，这个经常用在随机森林，不过据XGBoost的使用者反馈，列抽样防止过拟合的效果比传统的行抽样还好（xgboost也提供行抽样的参数供用户使用），并且有利于后面提到的并行化处理算法。

查找分裂点的近似算法 Approximate Algorithm

主要参考论文3.2节

当数据量十分庞大，以致于不能全部放入内存时，精确的贪婪算法就不可能很有效率，通样的问题也出现在分布式的数据集中，为了高效的梯度提升算法，在这两种背景下，近似的算法被提出使用，算法的伪代码如下图所示

概括一下：枚举所有特征，根据特征，比如是第 $k$ 个特征的分布的分位数来决定出 $l$ 个候选切分点 $S_k=\{s_{k1},s_{k2},\cdots s_{kl}\}$ ，然后根据这些候选切分点把相应的样本映射到对应的桶中，对每个桶的 $G,H$ 进行累加。最后在候选切分点集合上贪心查找，和Exact Greedy Algorithm类似。

特征分布的分位数的理解

此图来自知乎weapon大神的《 GBDT算法原理与系统设计简介》

论文给出近似算法的2种变体，主要是根据候选点的来源不同区分：

1. 在建树之前预先将数据进行全局（global）分桶，需要设置更小的 ϵ ，产生更多的桶，特征分裂查找基于候选点多，计算较慢，但只需在全局执行一次，全局分桶多次使用。
2. 每次分裂重新局部（local）分桶，可以设置较大的 ϵ ，产生更少的桶，每次特征分裂查找基于较少的候选点，计算速度快，但是需要每次节点分裂后重新执行，论文中说该方案更适合树深的场景。

论文给出Higgs案例下，方案1全局分桶设置 ϵ=0.05 与精确算法效果差不多，方案2局部分桶设置 ϵ=0.3 与精确算法仅稍差点，方案1全局分桶设置 ϵ=0.3 则效果极差，如下图：

由此可见，局部选择的近似算法的确比全局选择的近似算法优秀的多，所得出的结果和贪婪算法几乎不相上下。

最后很重的是：使用哪种方案，xgboost用户可以自由选择。

Notably, it is also possible to directly construct approximate histograms of gradient statistics. Our system efficiently supports exact greedy for the single machine setting, as well as approximate algorithm with both local and global proposal methods for all settings. Users can freely choose between the methods according to their needs.

这里直方图算法，常用于GPU的内存优化算法，leetcode上也有人总结出来：LeetCode Largest Rectangle in Histogram O(n) 解法详析， Maximal Rectangle

带权的分位方案 Weighted Quantile Sketch

主要参考论文3.3节

在近似的分裂点查找算法中，一个步骤就是提出候选分裂点，通常情况下，一个特征的分位数使候选分裂点均匀地分布在数据集上，就像前文举的关于特征分位数的例子。

考虑 KaTeX parse error: Expected 'EOF', got '\cal' at position 1: \̲c̲a̲l̲{D}_k = \lbrace… 代表每个样本的第 $k$ 个特征和其对应的二阶梯度所组成的集合。那么我们现在就能用分位数来定义下面的这个排序函数 $r_k:\mathbb{R}\to [0,1]$
KaTeX parse error: Expected '}', got '\cal' at position 36: …sum_{(x,h) \in \̲c̲a̲l̲{D}_k}h} \sum_{…
上式表示的就是该特征的值小于 $z$ 的样本所占总样本的比例。于是我们就能用下面这个不等式来寻找分裂候选点$\{s_{k1},s_{k2},s_{k3},\cdots ,s_{kl}\}$
$$\Vert r_k(s_{k,j})-r_k(s_{k,j+1})\Vert <ϵ,s_{k1}=\underset{i}{\min }{x}_{ik},s_{kl}=\underset{i}{\max }{x}_{ik}$$
上式中 $ϵ$ 的作用：控制让相邻两个候选分裂点相差不超过某个值 $ϵ$ ，那么 $1/ϵ$ 的整数值就代表几分位，举例 $ϵ=1/3$ ，那么就是三分位，即有 $3-1$ 个候选分裂点。数学上，从最小值开始，每次增加 KaTeX parse error: Got function '\max' as argument to '\underset' at position 16: ϵ∗(\underset{i}\̲m̲a̲x̲ ̲x_{ik}−\underse… 作为分裂候选点。然后在这些分裂候选点中选择一个最大分数作为最后的分裂点，而且每个数据点的权重是 $h_i$ ，原因如下：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Obj^{(t)} &\ap…
说明：这部分论文原文推导有些错误，国外问答网站 stack exchange 给出很明确的答复， 上式可以视为标签为 $-\frac{g_i}{h_i}$ 且权重为 $h_i$ 的平方误差，此时视 $\frac{g_i^2}{2h_i}$ 常数 （因为是来自上一轮的梯度和二阶梯度）。

现在应该明白 Weighted Quantile Sketch 带权的分位方案的由来，下面举个例子：

即要切分为3个，总和为1.8，因此第1个在0.6处，第2个在1.2处。此图来自知乎weapon大神的《 GBDT算法原理与系统设计简介》

注意稀疏问题的分裂点查找 Sparsity-aware Split Finding

主要参考论文3.4节

对于数据缺失数据、one-hot编码等造成的特征稀疏现象，作者在论文中提出可以处理稀疏特征的分裂算法，主要是对稀疏特征值缺失的样本学习出默认节点分裂方向：

1. 默认miss value进右子树，对non-missing value的样本在左子树的统计值 $G_L$ 与 $H_L$，右子树为 $G-G_L$ 与$H-H_L$，其中包含miss的样本。

2. 默认miss value进左子树，对non-missing value的样本在右子树的统计值 $G_R$ 与 $H_R$，左子树为 $G-G_R$ 与$H-H_R$ ，其中包含miss的样本。

这样最后求出增益最大的特征值以及miss value的分裂方向。作者在论文中提出基于稀疏分裂算法：

使用了该方法，相当于比传统方法多遍历了一次，但是它只在非缺失值的样本上进行迭代，因此其复杂度与非缺失值的样本成线性关系。在 Allstate-10k 数据集上，比传统方法快了50倍：

旨在并行学习的列块结构 Column Block for Parallel Learning

主要参考论文4.1节

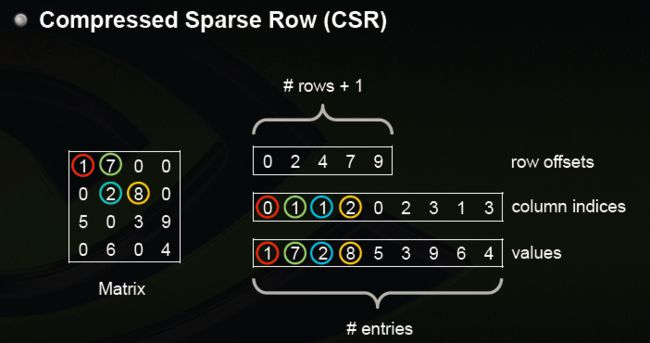
**CSR vs CSC **

稀疏矩阵的压缩存储形式，比较常见的其中两种：压缩的稀疏行（Compressed Sparse Row）和 压缩的稀疏列（Compressed Sparse Row）

CSR包含非0数据块values，行偏移offsets，列下标indices。offsets数组大小为（总行数目+1），CSR是对稠密矩阵的压缩，实际上直接访问稠密矩阵元素 (i,j) 并不高效，毕竟损失部分信息，访问过程如下：

    1. 根据行i 得到偏移区间开始位置 `offsets[i]`与区间结束位置 `offsets[i+1]-1`，得到ii行数据块 `values[offsets[i]..(offsets[i+1]-1)]`， 与非0的列下表`indices[offsets[i]..(offsets[i+1]-1)]`
    2. 在列下标数据块中二分查找j，找不到则返回0，否则找到下标值k，返回values[offsets[i]+k]

从访问单个元素来说，从 $O(1)$ 时间复杂度升到 $O(\log N)$, N 为该行非稀疏数据项个数。但是如果要遍历访问整行非0数据，则无需访问indices数组，时间复杂度反而更低，因为少了大量的稀疏为0的数据访问。

CSC与CSR变量结构上并无差别，只是变量意义不同，其中values仍然为非0数据块，offsets为列偏移，即特征id对应数组，indices为行下标，对应样本id数组，XBGoost使用CSC主要用于对特征的全局预排序。预先将CSR数据转化为无序的CSC数据，遍历每个特征，并对每个特征 i 进行排序：sort(&values[offsets[i]], &values[offsets[i+1]-1])。全局特征排序后，后期节点分裂可以复用全局排序信息，而不需要重新排序。

矩阵的存储形式，参考此文：稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB

采取这种存储结构的好处

未完待续。。。。。

关注缓存的存取 Cache-aware Access

使用Block结构的一个缺点是取梯度的时候，是通过索引来获取的，而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问，可能使得CPU cache缓存命中率低，从而影响算法效率。

因此，对于exact greedy算法中, 使用缓存预取。具体来说，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式在训练样本数大的时候特别有用，见下图：

在 approximate 算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的，设置过大则容易导致命中率低，过小则容易导致并行化效率不高。经过实验，发现 $2^{16}$ 比较好，那么上文提到CSC存储结构的 indices 数组（存储的行下表）的元素占用的字节数就是 16/8 = 2 。

核外块的计算 Blocks for Out-of-core Computation

XGBoost中提出Out-of-core Computation优化，解决了在硬盘上读取数据耗时过长，吞吐量不足

• 多线程对数据分块压缩 Block Compression，再将数据传输到内存，最后再用独立的线程解压缩，核心思想：将磁盘的读取消耗转换为解压缩所消耗的计算资源。
• 分布式数据库系统的常见设计：Block Sharding将数据分片到多块硬盘上，每块硬盘分配一个预取线程，将数据fetche到in-memory buffer中。训练线程交替读取多块缓存的同时，计算任务也在运转，提升了硬盘总体的吞吐量。

注：这部分内容属于外存算法External_memory_algorithm

XGBoost 对 GBDT 实现的巧妙之处

这部分内容主要参考了知乎上的一个问答 机器学习算法中 GBDT 和 XGBOOST 的区别有哪些？ - 知乎 根据他们的总结和我自己对论文的理解和补充。

1. 传统GBDT以CART作为基分类器，xgboost支持多种基础分类器。比如，线性分类器，这个时候xgboost相当于带 L1 和 L2正则化项 的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。

   可以通过booster [default=gbtree] 设置参数，详细参照官网

   • gbtree: tree-based models
   • gblinear: linear models
   • DART: Dropouts meet Multiple Additive Regression Trees dropout 在深度学习里面也经常使用，需要注意的是无论深度学习还是机器学习：使用droput训练出来的模型，预测的时候要使dropout失效。

2. 传统GBDT在优化时只用到一阶导数信息，xgboost则对损失函数函数进行了二阶泰勒展开，同时用到了一阶和二阶导数，这样相对会精确地代表损失函数的值。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导，详细参照官网API。

3. xgboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和，防止过拟合，这也是xgboost优于传统GBDT的一个特性。正则化的两个部分，都是为了防止过拟合，剪枝是都有的，叶子结点输出L2平滑是新增的。

4. Built-in Cross-Validation 内置交叉验证

XGBoost allows user to run a cross-validation at each iteration of the boosting process and thus it is easy to get the exact optimum number of boosting iterations in a single run.
This is unlike GBM where we have to run a grid-search and only a limited values can be tested.

9. continue on Existing Model 可以保存模型下次接着训练

User can start training an XGBoost model from its last iteration of previous run. This can be of significant advantage in certain specific applications.
GBM implementation of sklearn also has this feature so they are even on this point.

10. High Flexibility 可定制损失函数，只要这个损失函数2阶可导

XGBoost allow users to define custom optimization objectives and evaluation criteria.
This adds a whole new dimension to the model and there is no limit to what we can do.

xgboost工具支持并行。注意xgboost不同于随机森林中的并行粒度是：tree，xgboost与其他提升方法（比如GBDT）一样，也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

总体来说，这部分内容需要学习很多，特别是涉及到分布式地并发优化和资源调度算法，这就不仅仅是数学模型的问题了，还涉及到系统设计，程序运行性能的优化，本人实在是才疏学浅，这部分内容理解尚浅，进一步学习还需要其他论文和看XGBoost源码，有些优化的地方也不是作者首创，表示从附录的论文中得以学习集成到XGBoost中，真的是集万千之大作，作者不愧是上海交大ACM班出身。大神的访谈：https://cosx.org/2015/06/interview-of-tianqi/

优化的角度

马琳同学的回答 非常棒，真是让我感受到了：横看成岭侧成峰

高可用的xgboost

由于xgboost发展平稳成熟，现在已经非常易用，下图来自官网

hello world

来自官网，其他复杂的demo，参看github的demo目录

Python

import xgboost as xgb
# read in data
dtrain = xgb.DMatrix('demo/data/agaricus.txt.train')
dtest = xgb.DMatrix('demo/data/agaricus.txt.test')
# specify parameters via map
param = {'max_depth':2, 'eta':1, 'silent':1, 'objective':'binary:logistic' }
num_round = 2
bst = xgb.train(param, dtrain, num_round)
# make prediction
preds = bst.predict(dtest)

在jupter notebook中运行结果

import xgboost as xgb
# read in data
dtrain = xgb.DMatrix('demo/data/agaricus.txt.train')
dtest = xgb.DMatrix('demo/data/agaricus.txt.test')

[18:22:42] 6513x127 matrix with 143286 entries loaded from demo/data/agaricus.txt.train
[18:22:42] 1611x127 matrix with 35442 entries loaded from demo/data/agaricus.txt.test

# specify parameters via map
param = {'max_depth':3, 'eta':1, 'silent': 0, 'objective':'binary:logistic' }
num_round = 2
bst = xgb.train(param, dtrain, num_round)

[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\tree\updater_prune.cc:74: tree pruning end, 1 roots, 12 extra nodes, 0 pruned nodes, max_depth=3
[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\tree\updater_prune.cc:74: tree pruning end, 1 roots, 10 extra nodes, 0 pruned nodes, max_depth=3

# make prediction
preds = bst.predict(dtest)
print(preds)
print(bst.eval(dtest))

[0.10828121 0.85500014 0.10828121 ... 0.95467216 0.04156424 0.95467216]
[0]	eval-error:0.000000

param = {'booster': 'dart',
         'max_depth': 4, 
         'eta': 0.001,
         'objective': 'binary:logistic', 
         'silent': 0,
         'sample_type': 'uniform',
         'normalize_type': 'tree',
         'rate_drop': 0.5,
         'skip_drop': 0.0}
#Command Line Parameters: 提升的轮次数
num_round = 2
bst = xgb.train(param, dtrain, num_round)

[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\tree\updater_prune.cc:74: tree pruning end, 1 roots, 18 extra nodes, 0 pruned nodes, max_depth=4
[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\gbm\gbtree.cc:494: drop 0 trees, weight = 1
[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\tree\updater_prune.cc:74: tree pruning end, 1 roots, 18 extra nodes, 0 pruned nodes, max_depth=4
[18:22:42] C:\Users\Administrator\Desktop\xgboost\src\gbm\gbtree.cc:494: drop 1 trees, weight = 0.999001

# make prediction
preds = bst.predict(dtest, ntree_limit=num_round)
print(preds)
print(bst.eval(dtest))

[0.4990105 0.5009742 0.4990105 ... 0.5009742 0.4990054 0.5009742]
[0]	eval-error:0.007449

参数详解

官网，看懂参数的前提是把前文数学公式和理论看懂，这部分内容主要是对官网的翻译。

运行XGBoost之前，我们必须设置3种类型的参数：通用参数（general parameters），提升器参数（booster paramter），任务参数（task parameter）。

1. 通用参数：与我们所使用的提升器（通常是树型提升器或者线性提升器）的提升算法相关。
2. 提升器参数：取决于你所选择的哪种提升器
3. 学习任务的参数：这些参数决定了学习的方案（learning scenario）。例如：在排名任务场景下，回归任务可能使用不同的参数。
4. 命令行参数：与 XGBoost 的命令行接口（CLI）版本的行为相关。

Note

Parameters in R package

In R-package, you can use . (dot) to replace underscore(与underline同义) in the parameters, for example, you can use max.depth to indicate max_depth. The underscore parameters are also valid in R.

• General Parameters
  • Parameters for Tree Booster
  • Additional parameters for Dart Booster (booster=dart)
  • Parameters for Linear Booster (booster=gblinear)
  • Parameters for Tweedie Regression (objective=reg:tweedie)
• Learning Task Parameters
• Command Line Parameters

通用参数 general parameters

1. booster [default=gbtree] 设定基础提升器的参数

   Which booster to use. Can be gbtree, gblinear or dart; gbtree and dart use tree based models while gblinear uses linear functions.

2. silent [default=0]: 设置成1则没有运行信息的输出，最好是设置为0.

3. nthread [default to maximum number of threads available if not set]：线程数

4. disable_default_eval_metric [default=0]
   Flag to disable default metric. Set to >0 to disable. ，使默认的模型评估器失效的标识

5. num_pbuffer [set automatically by XGBoost, no need to be set by user]
   Size of prediction buffer, normally set to number of training instances. The buffers are used to save the prediction results of last boosting step.

6. num_feature [set automatically by XGBoost, no need to be set by user]
   Feature dimension used in boosting, set to maximum dimension of the feature

提升器参数 Booster parameters

树提升器参数 Parameters for Tree Booster

1. eta [default=0.3], range $[0,1]$

   shrinkage参数，用于更新叶子节点权重时，乘以该系数，避免步长过大。参数值越大，越可能无法收敛。把学习率 eta 设置的小一些，小学习率可以使得后面的学习更加仔细。

2. gamma [default=0 alias: min_split_loss] , range $[0,\infty ]$

   功能与min_split_loss 一样，（alias是“别名，又名”的意思，联想linux命令：alias就非常容易理解，即给相应的命令起了新的名字，引用是同一段功能的同一个程序是一样）后剪枝时，用于控制是否后剪枝的参数。

3. max_depth [default=6], range $[0,\infty ]$

   每颗树的最大深度，树高越深，越容易过拟合。

4. min_child_weight [default=1], range: $[0,\infty ]$

   这个参数默认是 1，是每个叶子里面loss函数二阶导（ hessian）的和至少是多少，对正负样本不均衡时的 0-1 分类而言，假设 h 在 0.01 附近，min_child_weight 为 1 意味着叶子节点中最少需要包含 100 个样本。这个参数非常影响结果，控制叶子节点中二阶导的和的最小值，该参数值越小，越容易 overfitting。

5. max_delta_step [default=0] , range: $[0,\infty ]$

   这个参数在更新步骤中起作用，如果取0表示没有约束，如果取正值则使得更新步骤更加保守。可以防止做太大的更新步子，使更新更加平缓。

6. subsample [default=1], range: $[0,1]$

   训练实例的抽样率，较低的值使得算法更加保守，防止过拟合，但是太小的值也会造成欠拟合。如果设置0.5，那就意味着随机树的生长之前，随机抽取训练数据的50%做样本。

7. colsample_bytree [default=1], range: $[0,1]$

   在构建每棵树的时候，特征（这里说是列，因为样本是按行存储的，那么列就是相应的特征）的采样率，用的特征进行列采样.

8. colsample_bytree 表示的是每次分割节点时，抽取特征的比例。

9. lambda [default=1, alias: reg_lambda]

   作用于权重值的 L2 正则化项参数，参数越大，模型越不容易过拟合。

10. alpha [default=0, alias: reg_alpha]

    作用于权重值的 L1 正则项参数，参数值越大，模型越不容易过拟合。

11. tree_method string [default=auto]

    • 用来设定树的构建算法，欲知详情请看陈天奇论文中的引用资料： reference paper.

      The tree construction algorithm used in XGBoost. See description in the reference paper.

    • 分布式和外存版本仅仅支持 tree_method=approx

      Distributed and external memory version only support tree_method=approx.

    • 选项：auto, exact, approx, hist, gpu_exact, gpu_hist, auto

      Choices: auto,exact,approx,hist,gpu_exact,gpu_hist,auto

      • auto: Use heuristic to choose the fastest method. 启发式地选择快速算法
        ​ - For small to medium dataset, exact greedy (exact) will be used. 中小数据量采用精确的贪婪搜索算法（指代前文说的树的生长过程中，节点分裂算法，所以很好理解）
        ​ - For very large dataset, approximate algorithm (approx) will be chosen. 非常大的数据集，近似算法将被选用。
        ​ - Because old behavior is always use exact greedy in single machine, user will get a message when approximate algorithm is chosen to notify this choice. 因为旧的行为总是使用精确的贪婪算法，所以在近似算法被选用的时候，用户会收到一个通知消息，告诉用户近似算法被选用。

        • exact: Exact greedy algorithm. 精确地贪婪算法

        • approx: Approximate greedy algorithm using quantile sketch and gradient histogram. 近似算法采用分位方案和梯度直方图方案。

        • hist: Fast histogram optimized approximate greedy algorithm. It uses some performance improvements such as bins caching. 优化过的近似贪婪算法的快速算法，这个快速算法采用一些性能改善（的策略），例如桶的缓存（这里桶指的是直方图算法中所用的特征数据划分成不同的桶，欲知详情，查看陈天奇论文以及论文的引用资料）

        • gpu_exact: GPU implementation of exact algorithm.

        • gpu_hist: GPU implementation of hist algorithm.

12. sketch_eps [default=0.03], range: (0, 1) 全称：sketch epsilon 即 分位算法中的 $ϵ$ 参数

    - Only used for `tree_method=approx`. 仅仅用于近似算法
    - This roughly translates into `O(1 / sketch_eps)` number of bins. Compared to directly select number of bins, this comes with theoretical guarantee with sketch accuracy. 大致理解为桶数的倒数值。与直接给出桶数相比，这个与带权分位草案（Weighted Quantitle Sketch）能够保证理论上一致，此部分内容详询陈天奇论文3.3节
    - **Usually user does not have to tune this**. But consider setting to a lower number for more accurate enumeration of split candidates. 通常情况下，不需要用户调试这个参数，但是考虑到设置一个更低的值能够枚举更精确的分割候选点。
    

13. scale_pos_weight [default=1] 正标签的权重缩放值

    • Control the balance of positive and negative weights, useful for unbalanced classes. A typical value to consider: sum(negative instances) / sum(positive instances). 控制样本正负标签的平衡，对于标签不平衡的样本有用，一个经典的值是：训练样本中具有负标签的实例数量/训练样本中正标签的实例数量。（举例：-1:2000个 +1:8000个，那么训练过程中每个正标签实例权重只有负标签实例的25%）

      See Parameters Tuning for more discussion. Also, see Higgs Kaggle competition demo for examples: R, py1, py2, py3.

14. updater [default=grow_colmaker,prune] 逗号分割的字符串定义树的生成器和剪枝，注意这些生成器已经模块化，只要指定名字即可。

    • A comma separated string defining the sequence of tree updaters to run, providing a modular way to construct and to modify the trees. This is an advanced parameter that is usually set automatically, depending on some other parameters. However, it could be also set explicitly by a user. The following updater plugins exist:
      • grow_colmaker: non-distributed column-based construction of trees. 单机版本下的基于列数据生长树，这里distributed tree 是xgboost有两种策略：单机版non-distributed和distributed分布式版本，比如单机版用的是精确贪婪的方式寻找分割数据点，分布式版本在采用的是近似直方图算法）
      • distcol: distributed tree construction with column-based data splitting mode. 用基于列数据的分割模式来构建一个树（即：生长一棵树），且树是按照分布式版本的算法构建的。
      • grow_histmaker: distributed tree construction with row-based data splitting based on global proposal of histogram counting. 基于全局数据的直方图统计信息，并按照行分割的方式地进行树的生长。
      • grow_local_histmaker: based on local histogram counting. 基于局部数据（当前节点，非整棵树）的直方图统计
      • grow_skmaker: uses the approximate sketching algorithm. 使用近似草案算法。
      • sync: synchronizes trees in all distributed nodes. 在分布式地所有节点中同步树（的信息）
      • refresh: refreshes tree’s statistics and/or leaf values based on the current data. Note that no random subsampling of data rows is performed. 刷新树的统计信息或者基于当前数据的叶子节点的值，注意：没有进行数据行的随机子抽样。
      • prune: prunes the splits where loss < min_split_loss (or $\gamma$). 在当前节点小于被定义的最小分割损失时，那么进行剪枝。
    • In a distributed setting, the implicit updater sequence value would be adjusted to grow_histmaker,prune.在分布式环境下，这个参数值被显示地调整为grow_histmaker,prune

15. refresh_leaf [default=1]

    • This is a parameter of the refresh updater plugin. When this flag is 1, tree leafs as well as tree nodes’ stats are updated. When it is 0, only node stats are updated. 用来标记是否刷新叶子节点信息的标识。当这个标志位为0时，只有节点的统计信息被更新。

16. process_type [default=default]

    • A type of boosting process to run.
    • Choices:default,update
      • default: The normal boosting process which creates new trees.
      • update: Starts from an existing model and only updates its trees. In each boosting iteration, a tree from the initial model is taken, a specified sequence of updater plugins is run for that tree, and a modified tree is added to the new model. The new model would have either the same or smaller number of trees, depending on the number of boosting iteratons performed. Currently, the following built-in updater plugins could be meaningfully used with this process type: refresh, prune. With process_type=update, one cannot use updater plugins that create new trees.

17. grow_policy [default=depthwise] 树的生长策略，基于深度或者基于最高损失变化

    • Controls a way new nodes are added to the tree.
    • Currently supported only if tree_method is set to hist.
    • Choices:depthwise, lossguide
      • depthwise: split at nodes closest to the root. 按照离根节点最近的节点进行分裂
      • lossguide: split at nodes with highest loss change.

18. max_leaves [default=0] 叶子节点的最大数目，只有当参数``grow_policy=lossguide`才相关（起作用）

    • Maximum number of nodes to be added. Only relevant when grow_policy=lossguide is set.

19. max_bin, [default=256] 桶的最大数目

    • Only used if tree_method is set to hist.只有参数 tree_method=hist 时，这个参数才被使用。
    • Maximum number of discrete bins to bucket continuous features. 用来控制将连续特征离散化为多个直方图的直方图数目。
    • Increasing this number improves the optimality of splits at the cost of higher computation time. 增加此值提高了拆分的最优性, 但是是以更多的计算时间为代价的。

20. predictor , [default=cpu_predictor] 设定预测器算法的参数

    • The type of predictor algorithm to use. Provides the same results but allows the use of GPU or CPU.
      • cpu_predictor: Multicore CPU prediction algorithm. 多核cpu预测器算法
      • gpu_predictor: Prediction using GPU. Default when tree_method is gpu_exact or gpu_hist. GPU预测器算法，当参数 tree_method = gpu_exact or gpu_hist 时，预测器算法默认采用 gpu_predictor 。

Additional parameters for Dart Booster (booster=dart)

Note 在测试集上预测的时候，必须通过参数 ntree_limits 要关闭掉dropout功能

Using predict() with DART booster

If the booster object is DART type, predict() will perform dropouts, i.e. only some of the trees will be evaluated. This will produce incorrect results if data is not the training data. To obtain correct results on test sets, set ntree_limit to a nonzero value, e.g.

preds = bst.predict(dtest, ntree_limit=num_round)

• sample_type [default=uniform] 设定抽样算法的类型

  • Type of sampling algorithm.
    • uniform: dropped trees are selected uniformly. 所有的树被统一处理，指的是权重一样，同样的几率被选为辍学树（被选为辍学的树，即不参与训练的学习过程）
    • weighted: dropped trees are selected in proportion to weight. 选择辍学树的时候是正比于权重。

• normalize_type [default=tree] 归一化（又名：标准化）算法的的类型，这个地方是与深度学习中的dropout不太一样。

  • Type of normalization algorithm.
    • tree: new trees have the same weight of each of dropped trees. 新树拥有跟每一颗辍学树一样的权重
      • Weight of new trees are 1 / (k + learning_rate).
      • Dropped trees are scaled by a factor of k / (k + learning_rate).
    • forest: new trees have the same weight of sum of dropped trees (forest).新树的权重等于所有辍学树的权重总和
      • Weight of new trees are 1 / (1 + learning_rate).
      • Dropped trees are scaled by a factor of 1 / (1 + learning_rate).

• rate_drop [default=0.0], range: [0.0, 1.0] 辍学率，与深度学习中的一样意思

  • Dropout rate (a fraction of previous trees to drop during the dropout).

• one_drop [default=0] 设置是否在选择辍学的过程中，至少一棵树被选为辍学树。

  • When this flag is enabled, at least one tree is always dropped during the dropout (allows Binomial-plus-one or epsilon-dropout from the original DART paper).

• skip_drop [default=0.0], range: [0.0, 1.0] 在提升迭代的过程中，跳过辍学过程的概率，即不执行dropout功能的概率

  • Probability of skipping the dropout procedure during a boosting iteration.
    • If a dropout is skipped, new trees are added in the same manner as gbtree.
    • Note that non-zero skip_drop has higher priority than rate_drop or one_drop. 注意到非0值得skip_drop参数比rate_drop和one_drop参数拥有更高的优先级。

学习任务的参数 Learning Task Parameters

Specify the learning task and the corresponding learning objective. The objective options are below:

• objective[default=reg:linear] 这个参数定义需要被最小化的损失函数

  • reg:linear: linear regression

  • reg:logistic: logistic regression

  • binary:logistic: logistic regression for binary classification, output probability

  • binary:logitraw: logistic regression for binary classification, output score before logistic transformation

  • binary:hinge: hinge loss for binary classification. This makes predictions of 0 or 1, rather than producing probabilities.

  • gpu:reg:linear, gpu:reg:logistic, gpu:binary:logistic, gpu:binary:logitraw: versions of the corresponding objective functions evaluated on the GPU; note that like the GPU histogram algorithm, they can only be used when the entire training session uses the same dataset

  • count:poisson
    –poisson regression for count data, output mean of poisson distribution

    • max_delta_step is set to 0.7 by default in poisson regression (used to safeguard optimization)

  • survival:cox: Cox regression for right censored survival time data (negative values are considered right censored). Note that predictions are returned on the hazard ratio scale (i.e., as HR = exp(marginal_prediction) in the proportional hazard function h(t) = h0(t) * HR). 比例风险回归模型(proportional hazards model，简称Cox模型)” 这块不太懂

  • multi:softmax: set XGBoost to do multiclass classification using the softmax objective, you also need to set num_class(number of classes)

  • multi:softprob: same as softmax, but output a vector of ndata * nclass, which can be further reshaped to ndata * nclass matrix. The result contains predicted probability of each data point belonging to each class.

  • rank:pairwise: Use LambdaMART to perform pairwise ranking where the pairwise loss is minimized

  • rank:ndcg: Use LambdaMART to perform list-wise ranking where Normalized Discounted Cumulative Gain (NDCG) is maximized

  • rank:map: Use LambdaMART to perform list-wise ranking where Mean Average Precision (MAP) is maximized

  • reg:gamma: gamma regression with log-link. Output is a mean of gamma distribution. It might be useful, e.g., for modeling insurance claims severity, or for any outcome that might be gamma-distributed.

  • reg:tweedie: Tweedie regression with log-link. It might be useful, e.g., for modeling total loss in insurance, or for any outcome that might be Tweedie-distributed.

• base_score [default=0.5]

  • The initial prediction score of all instances, global bias
  • For sufficient number of iterations, changing this value will not have too much effect.

• eval_metric [default according to objective] 对于有效数据的度量方法

  • Evaluation metrics for validation data, a default metric will be assigned according to objective (rmse for regression, and error for classification, mean average precision for ranking)
  • User can add multiple evaluation metrics. Python users: remember to pass the metrics in as list of parameters pairs instead of map, so that latter eval_metric won’t override previous one
  • The choices are listed below:
    • rmse: root mean square error 均方根误差
    • mae: mean absolute error 平均绝对误差
    • logloss: negative log-likelihood 负对数似然函数值
    • error: Binary classification error rate. It is calculated as #(wrong cases)/#(all cases). For the predictions, the evaluation will regard the instances with prediction value larger than 0.5 as positive instances, and the others as negative instances. 二分类错误率(阈值为0.5)
    • error@t: a different than 0.5 binary classification threshold value could be specified by providing a numerical value through ‘t’指定2分类误差率的阈值t
    • merror: Multiclass classification error rate. It is calculated as #(wrong cases)/#(all cases). 多分类错误率
    • mlogloss: Multiclass logloss. 多分类的负对数似然函数值
    • auc: Area under the curve 曲线下面积
    • aucpr: Area under the PR curve 准确率和召回率曲线下的面积
    • ndcg: Normalized Discounted Cumulative Gain
    • map: Mean Average Precision 主集合的平均准确率(MAP)是每个主题的平均准确率的平均值
    • ndcg@n, map@n: ‘n’ can be assigned as an integer to cut off the top positions in the lists for evaluation.
    • ndcg-, map-, ndcg@n-, map@n-: In XGBoost, NDCG and MAP will evaluate the score of a list without any positive samples as 1. By adding “-” in the evaluation metric XGBoost will evaluate these score as 0 to be consistent under some conditions.
    • poisson-nloglik: negative log-likelihood for Poisson regression
    • gamma-nloglik: negative log-likelihood for gamma regression
    • cox-nloglik: negative partial log-likelihood for Cox proportional hazards regression
    • gamma-deviance: residual deviance for gamma regression
    • tweedie-nloglik: negative log-likelihood for Tweedie regression (at a specified value of the tweedie_variance_power parameter)

• seed [default=0] 随机数的种子

  • Random number seed. 设置它可以复现随机数据的结果，也可以用于调整参数

命令行参数 Command Line Parameters

The following parameters are only used in the console version of XGBoost

• num_round
  • The number of rounds for boosting
• data
  • The path of training data
• test:data
  • The path of test data to do prediction
• save_period [default=0]
  • The period to save the model. Setting save_period=10 means that for every 10 rounds XGBoost will save the model. Setting it to 0 means not saving any model during the training.
• task [default=train] options:train,pred,eval,dump
  • train: training using data
  • pred: making prediction for test:data
  • eval: for evaluating statistics specified by eval[name]=filename
  • dump: for dump the learned model into text format
• model_in [default=NULL]
  • Path to input model, needed for test, eval, dump tasks. If it is specified in training, XGBoost will continue training from the input model.
• model_out [default=NULL]
  • Path to output model after training finishes. If not specified, XGBoost will output files with such names as 0003.model where 0003 is number of boosting rounds.
• model_dir [default=models/]
  • The output directory of the saved models during training
• fmap
  • Feature map, used for dumping model
• dump_format [default=text] options:text, json
  • Format of model dump file
• name_dump [default=dump.txt]
  • Name of model dump file
• name_pred [default=pred.txt]
  • Name of prediction file, used in pred mode
• pred_margin [default=0]
  • Predict margin instead of transformed probability
    XGBoost GPU Support
    XGBoost Python Package

调参

调参主要参考 Complete Guide to Parameter Tuning in XGBoost (with codes in Python) ，有空再详细说明。

引用

1. 陈天奇的论文 XGBoost: A Scalable Tree Boosting System
2. 陈天奇的演讲视频 XGBoost A Scalable Tree Boosting System June 02, 2016 演讲幻灯片 和 官网幻灯片
3. XGBoost 官网
4. XGBoost的贡献者之一的 演讲
5. 机器学习算法中 GBDT 和 XGBOOST 的区别有哪些？ - 知乎