深度学习之DeepFM实操演练

DeepFM原理

论文传送门

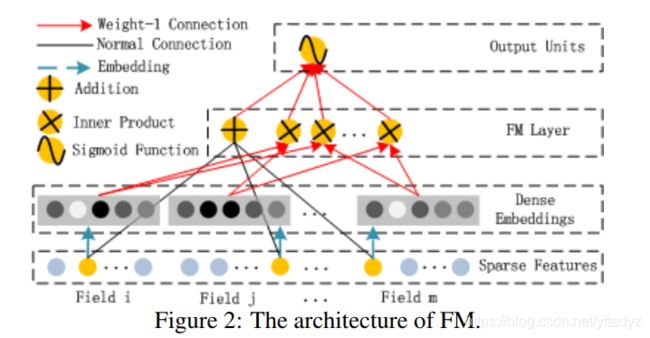
DeepFM使用Factorization Machine处理低阶特征组合，使用DNN处理高阶特征组合，然后将全部组合送入sigmoid或者softmax得到分类结果。

FM部分核心公式如下：

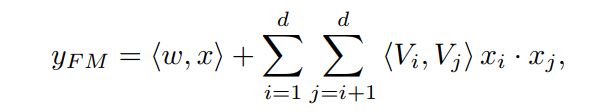
一阶特征，前面乘以一个系数w；二阶特征，考虑两个特征对应的embedding vectors，做内积即可。w和embedding vectors都是我们要学习的参数。

举个例子：
假设有三个特征：商品id，购买时间，评分，其中商品id有五个取值（‘001’,‘002’,‘003’,‘004’,‘005’），购买时间有两个取值(白天，夜晚)，评分有三个取值（好，一般，差）。有一条数据（‘002’,白天，好），它的one hot表示就为 one_hot =（0，1，0，0，0，1，0，1，0，0）,前五位对应商品id，中间两位对应购买时间，最后三位对应评分，总长度为10，即上面公式中的d=10。

再来看这个例子中我们要学习的参数，一阶特征组合系数$w=(w_0,w_1,...,w9)$，二阶特征组合系数由嵌入矩阵计算，商品id的嵌入矩阵 id_emb_mat:
$$id\_emb\_mat={\left[\begin{array}{c}id\_e_0\\ id\_e_1\\ id\_e_2\\ id\_e_3\\ id\_e_4\end{array}\right]}_{5\times K}$$， K为嵌入向量的维度。
同理购买时间的嵌入矩阵 time_emb_mat:
$$time\_emb\_mat={\left[\begin{array}{c}t\_e_0\\ t\_e_1\end{array}\right]}_{2\times K}$$

评分的嵌入矩阵rate_emb_mat:
$$rate\_emb\_mat={\left[\begin{array}{c}r\_e_0\\ r\_e_1\\ r\_e_2\end{array}\right]}_{3\times K}$$

那计算一下这个样本的$y_{FM}$吧。

$$\begin{array}{rl}{y}_{FM}& =w\cdot one\_hot+id\_e_1\cdot t\_e_0{}^T+id\_e_1\cdot r\_e_0{}^T+t\_e_0\cdot r\_e_0{}^T\end{array}$$

实现方法

实现方法上参考了ChenglongChen的版本（GitHub传送门）,这个版本的实现方法与论文的实现方法不同，它简化了模型的复杂度，只有一个嵌入矩阵，每个特征对应一个嵌入向量，而论文中是每个特征取值对应一个特征向量。

# ---------- first order term ----------
self.y_first_order = tf.nn.embedding_lookup(self.weights["feature_bias"], self.feat_index) # None * F * 1
self.y_first_order = tf.reduce_sum(tf.multiply(self.y_first_order, feat_value), 2)  # None * F
self.y_first_order = tf.nn.dropout(self.y_first_order, self.dropout_keep_fm[0]) # None * F

一阶特征直接将该特征的取值乘上一个feature_bias, 等价于将这个特征直接连接到输出单元softmax或signoid。

# ---------- second order term ---------------
# sum_square part
self.summed_features_emb = tf.reduce_sum(self.embeddings, 1)  # None * K
self.summed_features_emb_square = tf.square(self.summed_features_emb)  # None * K

# square_sum part
self.squared_features_emb = tf.square(self.embeddings)
self.squared_sum_features_emb = tf.reduce_sum(self.squared_features_emb, 1)  # None * K

# second order
self.y_second_order = 0.5 * tf.subtract(self.summed_features_emb_square, self.squared_sum_features_emb)  # None * K
self.y_second_order = tf.nn.dropout(self.y_second_order, self.dropout_keep_fm[1])  # None * K

二阶特征组合的计算方式与论文也有区别，更加简单。将每个特征的嵌入向量（要乘上该特征的取值）分别在嵌入向量的不同维度上面进行两两组合，输出结果的shape是[batch_size, K], K是嵌入向量维度。

我参考了这个版本，使用tf 2.2重新实现了一遍，算是加深一下对这个算法的理解吧（github传送门)。由于后面我想把它和RNN模块结合起来做一个通用性更强的、适用于营销场景的端到端模型，所以使用了字典切片作为模型输入（字典切片可以参考我的另一篇文章字典切片)。在一阶特征和二阶特征计算方法上没有做改动。

实操演练

数据集说明

演练使用的是titanic数据集，训练集有700条左右数据，测试集有300条左右，字段survived为1代表正样本，0代表负样本，找不到数据集的同学可以来[这里]。

建模过程

数据处理这块儿我做的毕竟简单，仅仅是处理了一下空值，然后对离散特征进行编码。

def preprocess(df,cate_cols,existed_cate=None):
    if not existed_cate:
        categories = {
     }
        for c in cate_cols:
            categories[c] = df[c].unique().tolist()
            
            #make sure 'unk' has code 0
            if 'unk' in categories[c]:
                categories[c].remove('unk')
            categories[c]=['unk']+categories[c]

            df[c] = pd.Categorical(df[c],
                                     categories=categories[c]).codes
        return categories
    else:
        for c in cate_cols:
            df[c] = pd.Categorical(df[c],
                                     categories=existed_cate[c]).codes
        return

字符型离散特征如果未知，我就标记为’unk’，数值型的所有特征，未知就记为0。如果特征取值为零的话，对应的嵌入向量就是零向量了，这个要注意一下。

y_train = dftrain.pop('survived')
y_eval = dfeval.pop('survived')

#transform dataframe to tensor
trainset=tf.data.Dataset.from_tensor_slices((dftrain.to_dict('list'),y_train.values))
evalset=tf.data.Dataset.from_tensor_slices((dfeval.to_dict('list'),y_eval.values))

#prepare batch set
batch_size=32
epoch_num=20
epoch_size=dftrain.shape[0]//batch_size
if dftrain.shape[0]%batch_size!=0:
    epoch_size+=1
trainset=trainset.shuffle(dftrain.shape[0]).batch(batch_size).repeat(epoch_num)
evalset=evalset.shuffle(dfeval.shape[0]).batch(128).repeat(1)

我比较喜欢tf.data.Dataset这个API，配合它的shuffle、batch、repeat这些方法，真的超级方便，当然要是输入毕较复杂的话，最好自己定义一个迭代器。

其他就是常规套路，adam优化器，BinaryCrossentropy损失函数，batch_size=32, 迭代了20个epoch，由于一个epoch只包含20个batch，所以实际上仅仅迭代了400 steps。

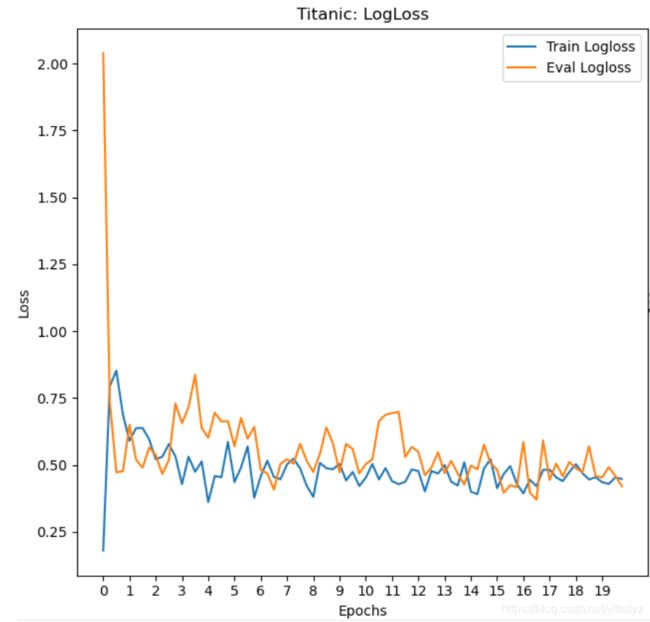
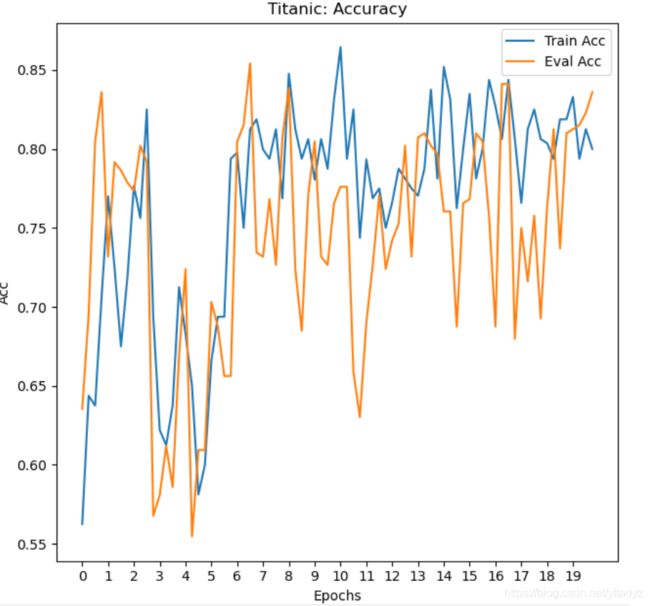
运行结果

可以看到测试集上的accuracy的波动还是非常大的，Accuracy最后能达到0.85左右。我们加上一个L2正则项，看看会有什么变化。

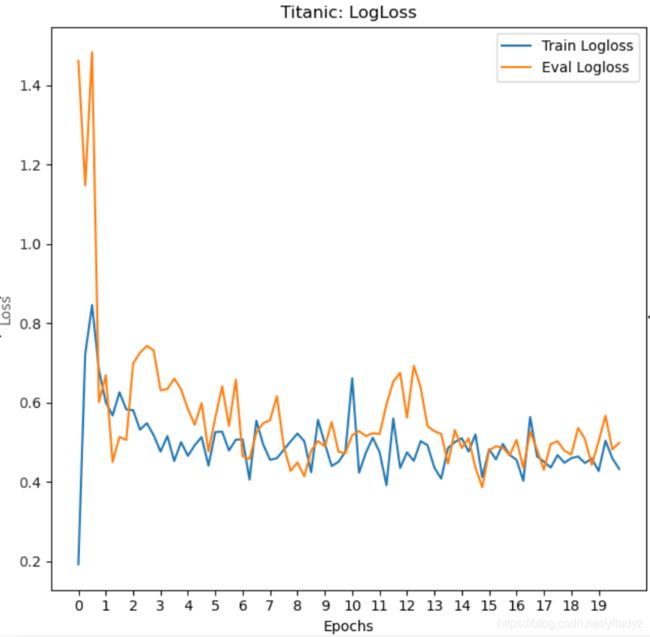
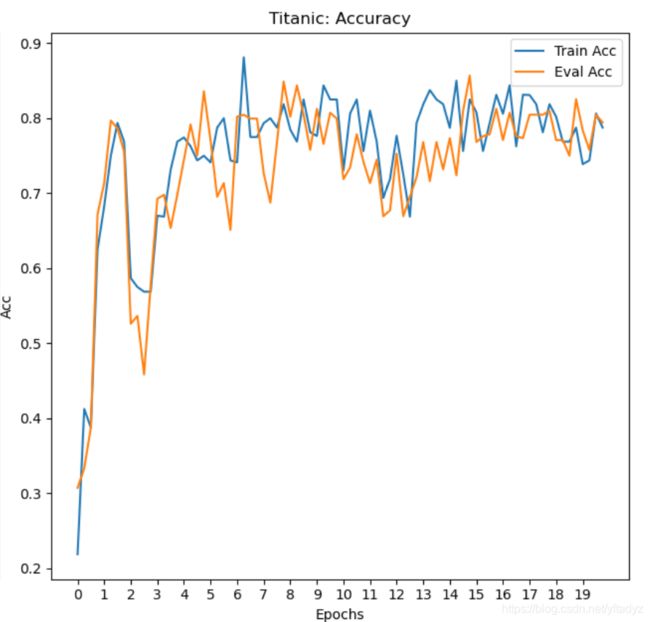
添加正则项后，振幅明显减弱了，效果也有提升，可以达到0.86左右。

后续计划

大多数营销应用场景，用户的数据既包括静态属性数据，也包括历史行为数据，DeepFM对静态属性数据的处理已经很出色了，我们还需要一个模块处理历史行为数据，从中提取出隐藏特征。如何实现，且听我下回分解~~

代码：
https://github.com/yftadyz/tensorflow2-DeepFM