数据结构与算法：01 绪论

绪论

知识结构：

---

一、什么是数据结构

例1：电话号码薄的查询问题。

$$(a_1,b_1),(a_2,b_2),\dots ,(a_n,b_n)$$

$a_i$：表示姓名，$b_i$：表示电话号码，$i=1,2,\dots ,n$。

思考：

• 怎样组织数据？
• 怎样存储数据？
• 怎样操作数据？
  • 添加操作
  • 删除操作
  • 修改操作
  • 查询操作
  • 排序操作
• 怎样代码实现？

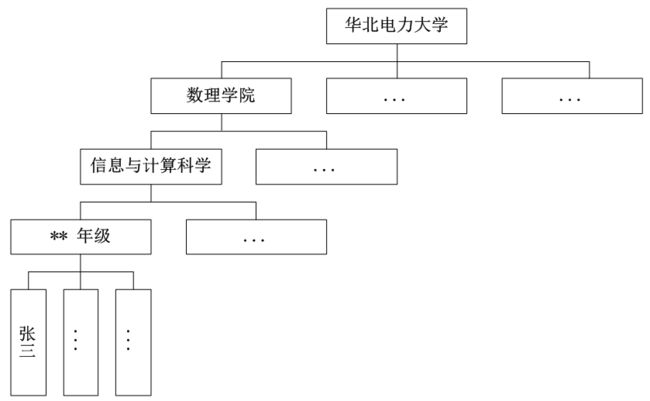
例2：学生自然情况查询问题。

思考：

• 怎样组织数据？
• 怎样存储数据？
• 怎样操作数据？
  • 添加操作
  • 删除操作
  • 修改操作
  • 查询操作
  • 排序操作
• 怎样代码实现？

数据结构的定义（Data Structure）

语言描述：数据结构是研究数据的逻辑结构，存储结构（物理结构）以及它们之间的关系，并对这种结构定义相适应的运算，设计出相应的算法。

形式化描述：数据结构是一个二元组

$$Data\_Struct=(D,R)$$

其中，$D$：是数据元素的有限集合， $R$：是$D$上关系的有限集合。

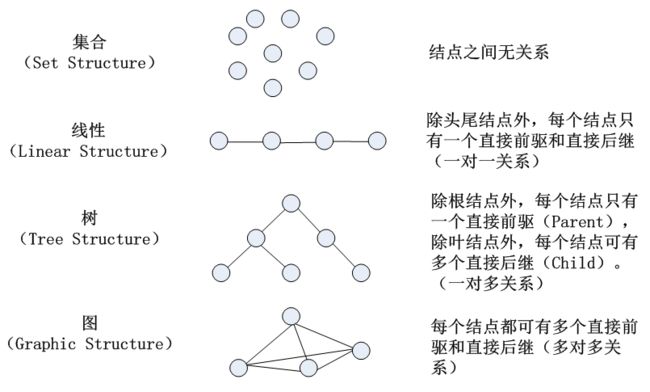
例3：集合结构。

$Set=(D,R)$ 其中，$D=\{ite{m}_1,ite{m}_2,ite{m}_3,ite{m}_4,itm{e}_5\}$，$R=\{\}$ （元素之间没有关系）。

比如：

• Python语言中的 Set
• C#语言中的 HashSet。

例4：线性结构。

$Line=(D,R)$其中，$R=\{<itm{e}_5,ite{m}_1>,<ite{m}_1,ite{m}_3>,<ite{m}_3,ite{m}_4>,<ite{m}_4,ite{m}_2>\}$（除了首尾结点，其余结点只有一个直接前驱，一个直接后继）。

比如：

• Numpy 中的ndarray
• C#语言中的数组
• Matlab中的矩阵

---

二、基本概念与术语

1、数据（Data）

指所有能输入计算机中并被计算机程序处理的符号集合。

可以是数值数据，如整数、实数；也可以是非数值数据，如字符、文字、图形、声音等。

2、数据元素（Data Element）

数据的基本单位，也称为结点，顶点，记录。

在计算机程序中，通常被作为一个整体进行考虑和处理。

3、数据项（Data Item）

具有独立含义的最小标识单位，也称为字段（Field）。

例如：在数据库信息处理系统中，数据表中的一条记录就是一个数据元素。这条记录中的学生学号、姓名、性别、籍贯、出生年月、成绩等字段就是数据项。

可见：数据由数据元素组成，数据元素由数据项组成。

4、逻辑结构（Logic Structure）

对数据之间逻辑关系的描述。（独立于计算机）

5、存储结构（Storage Structure）

逻辑结构在计算机存储器中的实现，即数据在计算机中的存放方式。

• 顺序：利用数组对数据进行存储。
• 链式：利用指针对数据进行存储。
• 索引：利用索引表来定位数据的存储。
• 散列：利用散列函数，根据数据元素关键字来定位数据的存储。

6、数据类型（Data Type）

数据类型是数据的取值范围和对数据进行操作的总和。

如：int、long、float、double、bool、char等

7、抽象数据类型（Abstract Data Type）

抽象数据类型由一组数据以及在该组数据上的一组操作组成。

抽象数据类型的格式定义如下：

ADT Name is
    Data
        构成该抽象数据类型所必须的基本数据项
    Operations
        Constructor
            Initial Values：赋给基本数据项的值
            Press：初始化对象
        Operation1
            Input：操作1要求用户输入的值
            PreCondition：系统执行操作1前的数据状态
            Press：操作1的解释说明
            Output：操作1结束后返回的数据
            PostCondition：系统执行操作1后的数据状态
        Operation2
            … …
        OperationN
            … …
End ADT Name

例5：矩形结构的ADT描述。

ADT Rectangle is
    Data
        float Length
        float Width
    Operations
        Constructor
            Initial Values：构造矩形时，赋长和宽的值。
            Press：初始化对象，给矩形的长和宽赋值。
        SetLength
            Input：赋给变量Length的新值
            PreCondition：无
            Press：将矩形的长度值修改为新值
            Output：无
            PostCondition：矩形的长度值被修改
        SetWidth
            Input：赋给变量Width的新值
            PreCondition：无
            Press：将矩形宽度值修改为新值
            Output：无
            PostCondition：矩形的宽度值被修改
        GetArea
            Input：无
            PreCondition：矩形的长度和宽度都大于零
            Press：得到矩形的面积
            Output：返回矩形面积的值
            PostCondition：无
        GetPerimeter
            Input：无
            PreCondition：矩形的长度和宽度都大于零
            Press：得到矩形的周长
            Output：返回矩形的周长
            PostCondition：无
End ADT Rectangle

一旦定义了矩形结构的ADT描述，就可以用代码进行实现了。

public class Rectangle
{
     
    public float Length;
    public float Width;
    public Rectangle(float length, float width)
    {
     
        Length = length > 0 ? length : 0f;
        Width = width > 0 ? width : 0f;
    }
    public void SetLength(float length)
    {
     
        Length = length > 0 ? length : 0f;
    }
    public void SetWidth(float width)
    {
     
        Width = width > 0 ? width : 0f;
    }
    public float GetArea()
    {
     
        if (Length * Width == 0)
            throw new ArgumentOutOfRangeException("长度或宽度为零。");
        return Length * Width;
    }
    public float GetPerimeter()
    {
     
        if (Length * Width == 0)
            throw new ArgumentOutOfRangeException("长度或宽度为零。");
        return (Length + Width) * 2;
    }
}

---

三、算法与算法分析

1、算法的基本概念

1.1 算法的定义

为了解决某类特定问题而提出的一组有穷规则，即以某些值或值的集合为输入并产生某些值或值的集合为输出的一系列运算步骤。

1.2 算法的五个重要特性

• 有穷性（Finity）：经过有限的时间可以完成。
• 确定性或无二义性（Unambiguousness）：给相同的输入，即得到相同的输出。
• 可行性（Realizability）
• 输入（Input）：至少有0个输入。
• 输出（Output）：至少1个。

1.3 算法设计的五点要求

• 正确性（Correctness）
• 可读性（Readability）
• 健壮性（Robustness）：具有很强的容错能力，对边界情况和异常情况做出处理。
• 运行时间（Running Time）
• 占用空间（Storage Space）：完成功能的前提下，时间越少，空间越小，越好。

1.4 算法与程序的区别

• 表现形式不同
  • 算法：自然语言、伪计算机语言等
  • 程序：计算机语言
• 是否具备有穷性

2、算法分析

2.1 时间复杂度（Time Complexity）

1）算法耗费的时间

一个算法耗费的时间 = 算法中每条语句的执行时间之和

每条语句的执行时间 = 语句的执行次数$\times$语句执行一次所需的时间

一般认为每条语句执行一次所需的时间是单位时间，即：一个算法耗费的时间 = 所有语句的执行频数之和

例6：计算方阵$A_{n\times n}\times B_{n\times n}$ 算法耗费的时间。

static double[,] MatrixMultiply(double[,] A, double[,] B, uint n)
{
     
    double[,] C = new double[n, n];             // 1
    for (int i = 0; i < n; i++)                 // n+1
    {
     
        for (int j = 0; j < n; j++)             // n*(n+1)
        {
     
            C[i, j] = 0;                        // n*n
            for (int k = 0; k < n; k++)         // n*n*(n+1)
            {
     
                C[i, j] += A[i, k] * B[k, j];   // n*n*n
            }
        }
    }
    return C;                                   // 1
}

$T(n)=2n^3+3n^2+2n+3$

2）问题的规模

算法求解问题的输入量，一般用一个整数表示。

• 矩阵求解问题，矩阵的阶数。
• 图论问题，图的结点个数，边的条数。

3）算法的时间复杂度 $T(n)$

就是该算法的时间耗费，是关于问题规模$n$的函数。

当$n\to \infty$时，与$T(n)$的同阶的简单函数称为算法的渐进时间复杂度。

例7： $T(n)=2n^3+3n^2+2n+3$

$\underset{n\to \infty }{\lim }\frac{2n^3+3n^2+2n+3}{n^3}=2$

所以 $T(n)=O(n^3)$

例8：针对一个问题，设计算法$A_1$，$A_2$其耗费时间$T_1(n)=100n^2$，$T_2(n)=n^3+n+1$，当$n\to \infty$时，$T_1(n)=O(n^2)$，$T_2(n)=O(n^3)$，即算法$A_1$所耗费的时间远小于算法$A_2$，在宏观上可通过渐进时间复杂度表示算法的优劣。

一般，我们把渐进时间复杂度$T(n)=O(f(n))$简称为时间复杂度。$f(n)$表示算法中频数最大语句的频数。

例9：

int x = 0;
int y = 0;
for (int i = 0; i < n; i++)
    x++;
for (int j = 0; j < n; j++)
    for (int k = 0; k < n; k++)
        y++;

$T(n)=O(n^2)$

例10：

int i = 50;
int j = 60;
int temp = i;
i = j;
j = temp;

$T(n)=O(1)$

4）常见的时间复杂度

• 常数阶：$O(1)$
• 对数阶：$O(log(n))$
• 线性阶：$O(n)$
• 线性对数阶：$O(nlog(n))$
• 平方阶：$O(n^2)$
• 立方阶：$O(n^3)$
• $k$方阶：$O(n^k)$
• 指数阶：$O(2^n)$

5）最坏时间复杂度

例11：在数组A[n]中查找给定值k。

static int Find(int[] A, int k)
{
     
    int i;
    for (i = 0; i < A.Length; i++) //(#)
        if (A[i] == k)
            break;
    return i == A.Length ? -1 : i;
}

• 当A中没有与k相等的元素，则(#)的频数$f(n)=n+1$；
• 当A中第1个元素与k相等，则(#)的频数$f(n)=1$；

最坏时间复杂度：最坏情况下的时间复杂度。

一般不特别说明，所讨论的时间复杂度，都指最坏时间复杂度。

2.2 空间复杂度（Space Complexity）

指该算法所耗费的存储空间，也是问题规模$n$的函数，渐进空间复杂度也常常称为空间复杂度。

---

后台回复「搜搜搜」，随机获取电子资源！
欢迎关注，请扫描二维码：