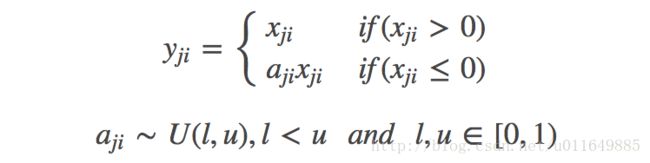浅析神经网络中的激活函数

1 什么是激活函数

激活函数就是一类x到y的映射
目的：是为了引入非线性元素，解决线性模型不能解决的问题。
意义：一个没有激活函数的神经网络将只不过是一个线性回归模型（Linear regression Model）。它并不能表达复杂的数据分布。

激活函数一般要满足的性质：
非线性：因为如果是线性激活函数，不管多少隐藏层，输出都是输入的线性组合。
可微性：因为当优化方法是基于梯度的时候，要对激活函数求偏导。
单调性：当激活函数是单调的时候，单层网络能够保证是凸函数。
输出值范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著。当激活函数输出值为无限的时候，模型的训练会更加高效，不过在这种情况下，一般需要更小的learning rate。

2 神经网络中为什么要使用激活函数？

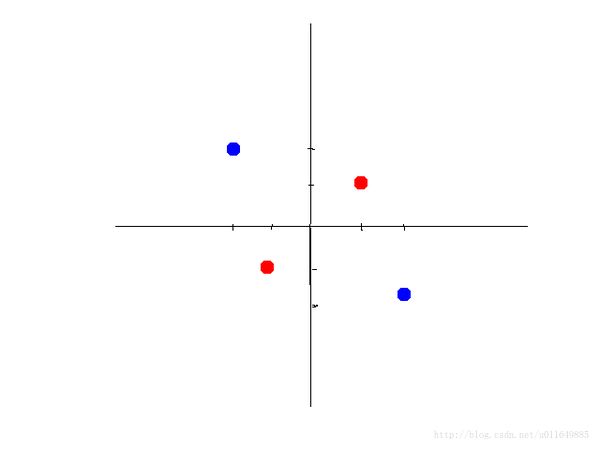
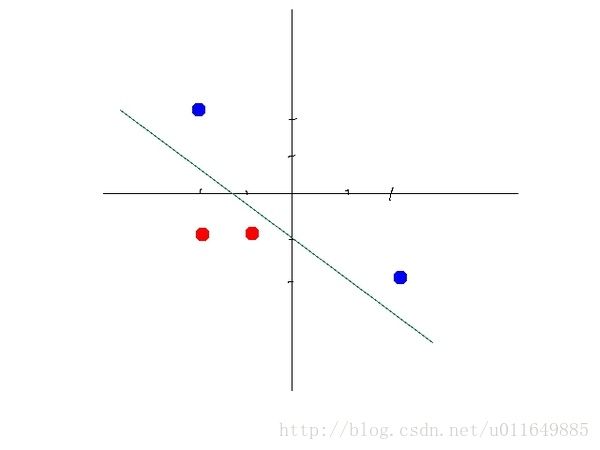
因为有些数据集并不是线性可分的。比如下面两幅图，左边是线性不可分，右边是线性可分。如果不用一个激活函数来处理，那这个神经网络什么时候也不能把左边这幅图的两种颜色的数据分开。

3 相关概念

饱和：当一个激活函数h(x)满足
limn→±∞ h ′(x)=0 我们称之为饱和了，n趋近于正无穷时为

硬饱和和软饱和：对任意的xx，如果存在常数cc，当x>cx>c时恒有 h′(x)=0h′(x)=0则称其为右硬饱和，当x

4 常用的激活函数

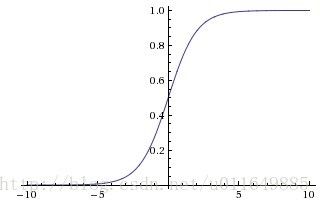
4.1 Sigmoid函数

sigmoid函数在浅层神经网络（三层）中使用比较多。

• 公式：

  f(x)=11+e−x

• 图像：

  

优点：
1、输出范围有限（0，1），在数据传递过程中不容易发散。所以可以作为输出层，输出表示概率。

缺点：
1、饱和导致容易产生梯度消失。sigmoid 神经元在值为 0 或 1 的时候接近饱和，这些区域，梯度几乎为 0。因此在反向传播时，这个局部梯度会与整个代价函数关于该单元输出的梯度相乘，结果也会接近为 0 。
这样，几乎就没有信号通过神经元传到权重再到数据了，因此这时梯度就对模型的更新没有任何贡献。导致信息丢失。
除此之外，为了防止饱和，必须对于权重矩阵的初始化特别留意。比如，如果初始化权重过大，那么大多数神经元将会饱和，导致网络就几乎不学习。
2、其输出并不是以0为中心的，这个特性会导致后面网络层的输入也不是0为中心的，进而影响梯度下降的运作。因为如果输入都是正数的话，那么关于梯度在反向传播过程中，要么全是正数，要么全是负数，这将会导致梯度下降权重更新时出现z字型下降。

---

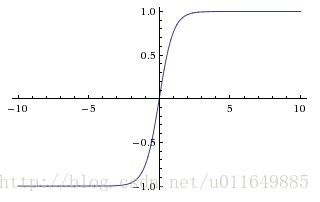
4.2 tanh（双曲正切）函数

• 公式：

  tanh(x)=$1+e−2x1−e−2x

• 图像：

  

优点：
1. 相比Sigmoid收敛速度更快。
2. 其输出以0为中心。

缺点：
和sigmoid函数一样，也是存在梯度消失的问题。

---

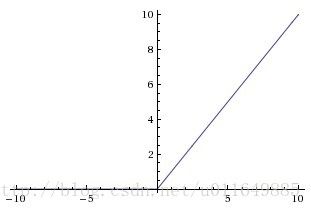
4.3 ReLU，目前使用最广泛的激活函数

• 公式：

  f(x)={0x(x≤0)(x>0)

• 图像：

  

优点：
1. 更容易学习优化，收敛速度比sigmoid/tanh快很多。因为其分段线性性质，导致其前传、后传，求导都是分段线性。
2. Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的互相依存关系，缓解了过拟合问题的发生。
3. 在生物上的合理性，它是单边的，相比sigmoid和tanh，更符合生物神经元的特征。

缺点：
1. ReLU在训练的时候很”脆弱”，一不小心有可能导致神经元”坏死”。举个例子：由于ReLU在x<0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，也就是ReLU神经元坏死了，不再对任何数据有所响应。实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都坏死了。 当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。

---

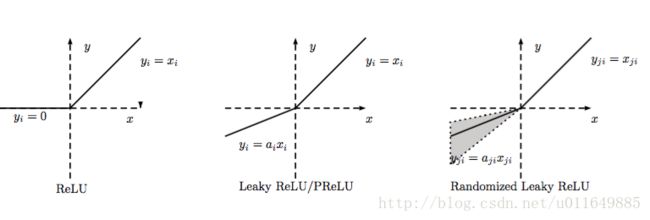
4.4 Leaky-ReLU、P-ReLU、R-ReLU

• LReLU和PReLU的函数：
  

  f(x)={yiaiyi(y_{i}>0)(y_{i}≤0)

• RReLU函数：

  

• LReLU
  当aiai比较小而且固定的时候，我们称之为LReLU。LReLU最初的目的是为了避免梯度消失。但在一些实验中，我们发现LReLU对准确率并没有太大的影响。很多时候，当我们想要应用LReLU时，我们必须要非常小心谨慎地重复训练，选取出合适的aa，LReLU的表现出的结果才比ReLU好。因此有人提出了一种自适应地从数据中学习参数的PReLU。

• PReLU
  PReLU是LReLU的改进，可以自适应地从数据中学习参数。PReLU具有收敛速度快、错误率低的特点。PReLU可以用于反向传播的训练，可以与其他层同时优化。

• RReLU
  其中， aij 是一个保持在给定范围内取样的随机变量，在测试中是固定的。RReLU在一定程度上能起到正则效果。

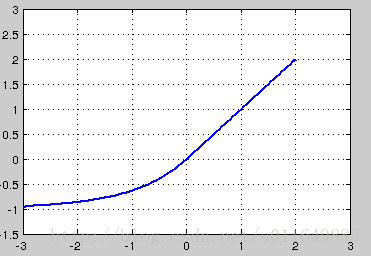
4.5 ELU

• 公式：
  f(x)={xα(ex−1)(x≥0)(x < 0)
• 图像：

优点：
1、融合了sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性。右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零，所以收敛速度更快。
2、将前面单元输入的激活值均值控制在0。
3、让激活函数的负值部分也可以被使用了。之前的激活函数，负值部分几乎不携带信息，特别是ReLU.

4.6 Maxout

f(x)=max(wT1x+b1,wT2x+b2,...,wTn+bn)

优点: maxout能够近似任意连续函数，且当w_{2},b_{2},…,w_{n},b_{n}为0时，退化为ReLU,Maxout同时能够缓解梯度消失，同时又规避了ReLU神经元死亡的缺点.
缺点: 增加了参数和计算量。

4.7 Softmax

fi(x)=exi∑Jj=1exjfori=1,....j

应用到多分类，把多个输入映射到0-1的数。

5 如何选择激活函数？

1） 4层以上就不要考虑sigmoid了，很容易出现梯度消失。
2）可以尝试tanh，但是层数多时tanh也会出现梯度消失。
3）使用ReLU激活函数时，注意不要把学习率设置太高，避免产生神经元“死亡”现象。
4）最好使用Maxout或者Leaky ReLU。

参考资料：

http://cs231n.github.io/neural-networks-1/
https://zhuanlan.zhihu.com/p/21462488
http://blog.csdn.net/cyh_24/article/details/50593400