Gamma分布与逆Gamma分布

Gamma分布与逆Gamma分布

Gamma分布

若随机变量X的密度函数为

⎧⎩⎨⎪⎪λαΓ(α)xα−1e−λx,x≥00,x<0GammaΓ(α)=∫+∞0xα−1e−xdx

则称X服从Gamma分布，记为X~ Ga(α,λ)

Gamma分布的期望和方差

E(x)=λαΓ(α)∫+∞0xαe−λxdx=Γ(α+1)Γ(α)1λ=αλE(x2)=λαΓ(α)∫+∞0xα+1e−λxdx=Γ(α+2)Γ(α)1λ2=α(α+1)λ2Var(x)=E(x2)−[E(x)]2=α(α+1)λ2−α2λ2=αλ2

其中期望式中的第二个等号处分别使用了 α 与 α+1 次分部积分法，与Gamma函数的性质： Γ(α)=(α−1)!

Gamma分布的特例

Ga(1,λ)=Exp(λ)=λe−λxGa(n2,12)=χ2(n)=(12)n2Γ(n2)xn2−1e−12x

Gamma分布与泊松分布、指数分布的关系
若一段时间[0,1]内事件A发生的次数服从参数为 λ 的泊松分布
两次事件发生的时间间隔将服从参数为 λ 的指数分布
n次事件发生的时间间隔服从X~ Ga(α,λ) 分布

——–

逆Gamma分布

若随机变量X的密度函数为：

⎧⎩⎨⎪⎪λαΓ(α)x−α−1exp(−λx),x≥00,x<0GammaΓ(α)=∫+∞0xα−1e−xdx

则称X服从InvGamma分布，记为 X~ IG(α,λ)

Gamma分布的期望和方差

E(x)=λαΓ(α)∫+∞0x−αe−λxdx=Γ(α−1)Γ(α)λ=λα−1E(x2)=λαΓ(α)∫+∞0x−α+1e−λxdx=Γ(α−2)Γ(α)λ2=λ2(α−1)(α−2)Var(x)=E(x2)−[E(x)]2=λ2(α−1)(α−2)−λ2(α−1)2=λ2(α−1)2(α−2)

其中期望式中的第二个等号处分别使用了 α 与 α+1 次分部积分法,与Gamma函数的性质： Γ(α)=(α−1)!

逆Gamma分布特例

IG(α2,αλ2)=Inv−χ2(α,λ)=(αλ2)α2Γ(α2)x−α2+1e−αλ2x

Gamma分布与逆Gamma分布
若随机变量X~ Ga(α,λ) ，则 1X ~ IG(α,λ)

——–

图像Python代码

Gamma分布

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
fig=plt.figure(figsize=(18,6))#确定绘图区域尺寸
ax1=fig.add_subplot(1,2,1)#将绘图区域分成左右两块
ax2=fig.add_subplot(1,2,2)
x=np.arange(0.01,15,0.01)#生成数列

z1=st.gamma.pdf(x,0.9,scale=2)#gamma(0.9,2)密度函数对应值
z2=st.gamma.pdf(x,1,scale=2)
z3=st.gamma.pdf(x,2,scale=2)
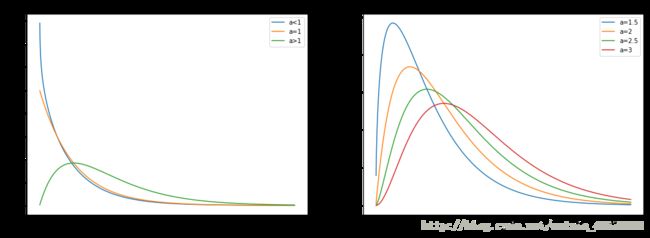
ax1.plot(x,z1,label="a<1")
ax1.plot(x,z2,label="a=1")
ax1.plot(x,z3,label="a>1")
ax1.legend(loc='best')
ax1.set_xlabel('x')
ax1.set_ylabel('p(x)')
ax1.set_title("Gamma Distribution lamda=2")

y1=st.gamma.pdf(x,1.5,scale=2)#gamma(1.5,2)密度函数对应值
y2=st.gamma.pdf(x,2,scale=2)
y3=st.gamma.pdf(x,2.5,scale=2)
y4=st.gamma.pdf(x,3,scale=2)
ax2.plot(x,y1,label="a=1.5")
ax2.plot(x,y2,label="a=2")
ax2.plot(x,y3,label="a=2.5")
ax2.plot(x,y4,label="a=3")
ax2.set_xlabel('x')
ax2.set_ylabel('p(x)')
ax2.set_title("Gamma Distribution lamda=2")
ax2.legend(loc="best")

plt.show()

逆Gamma分布

from scipy.stats import invgamma
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
a=[4,5,6]
for i in a:
    mean, var, skew, kurt = invgamma.stats(i,scale=2,moments='mvsk')
    x = np.linspace(invgamma.ppf(0.01,i,scale=2),invgamma.ppf(0.99,i,scale=2), 100)#invgamma.ppf
    ax.plot(x, invgamma.pdf(x,i,scale=2,), label="a="+str(i))
    ax.legend(loc="best")
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
ax.set_title("Invgamma Distribution lamda=2")
plt.show()