CUDA samples系列 0.6 matrixMul

矩阵相乘的代码，用的方法比较难理解，这部分我一步步画逻辑图来详细的展示下。

矩阵乘法

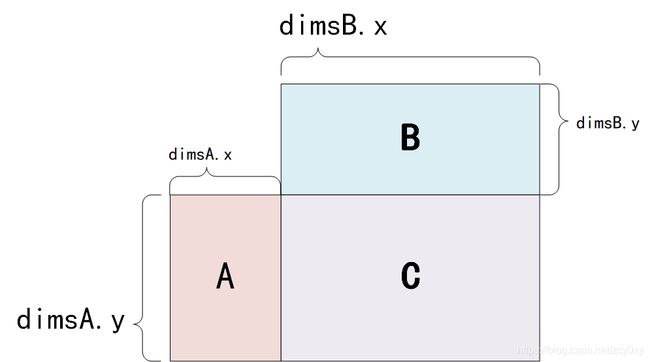
首先，矩阵乘法 A*B=C，A的行数等于B的列数，如下图所示
dimsA.x = dimsB.y，最后得到的C，尺寸为 [dimsA.y, dimsB.y]。

计算方法为A的第m行*B的第n列=C(m, n).

线程块的分配部署

程序对线程块，线程的任务分配如下。
block_size是程序设定的每个block含有多少个线程，源代码中设定为32.
矩阵是自己定义的，源代码定义大小为：

    dim3 dimsA(5*2*block_size, 5*2*block_size, 1);
    dim3 dimsB(5*4*block_size, 5*2*block_size, 1);

这里他把矩阵的长宽都设定为block_size的整数倍，这样方便下面的线程部署。
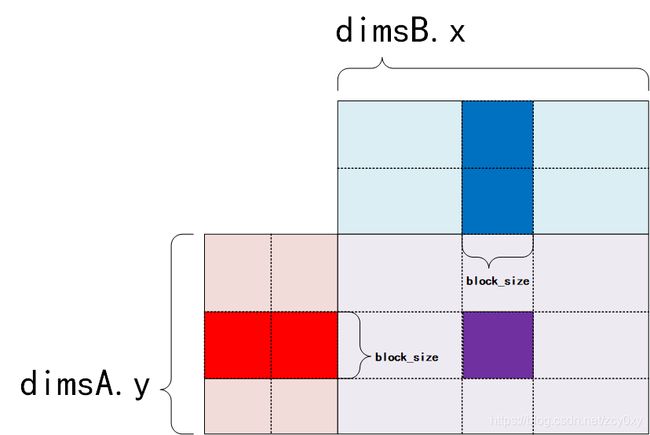
下图中A中红色的部分有block_size行，B中蓝色部分有block_size列，这两部分相乘得到C中紫色的部分，这部分大小为block_size*block_size。这个紫色的部分，全部由一个block计算得来，而一个线程则会负责紫色部分的一个元素：

核函数逻辑详解

先看一下核函数，发现里面有for，有aBegin，aEnd ，bBegin 等等，有点迷。
先别急，现在只要稳稳的记住一点，就是上面那个图，红色部分*蓝色部分=紫色部分，这些部分全部由一个block完成，并且每个block只负责这么多的部分。
每个thread负责计算出紫色区域（大小为block_size*block_size）中的一个点。

template <int BLOCK_SIZE> __global__ void
matrixMulCUDA(float *C, float *A, float *B, int wA, int wB)
{
    // Block index
    int bx = blockIdx.x;
    int by = blockIdx.y;
    // Thread index
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    int aBegin = wA * BLOCK_SIZE * by;
    int aEnd   = aBegin + wA - 1;
    int aStep  = BLOCK_SIZE;

    int bBegin = BLOCK_SIZE * bx;
    int bStep  = BLOCK_SIZE * wB;

    float Csub = 0;

    for (int a = aBegin, b = bBegin;
         a <= aEnd;
         a += aStep, b += bStep)
    {
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
        As[ty][tx] = A[a + wA * ty + tx];
        Bs[ty][tx] = B[b + wB * ty + tx];
        __syncthreads();

#pragma unroll
        for (int k = 0; k < BLOCK_SIZE; ++k)
        {
            Csub += As[ty][k] * Bs[k][tx];
        }
        __syncthreads();
    }

    int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
    C[c + wB * ty + tx] = Csub;
}

现在的关键是，这些for到底在干什么？每一个for内处理了多少数据？
再来好好看看这里：

    int aBegin = wA * BLOCK_SIZE * by;
    int aEnd   = aBegin + wA - 1;
    int aStep  = BLOCK_SIZE;

    int bBegin = BLOCK_SIZE * bx;
    int bStep  = BLOCK_SIZE * wB;

这里没有出现块内线程号tx和ty，只有线程块编号bx和by；也就意味着，对于一个block里的所有线程，这五个参数计算出来的是一样的。

int aBegin = wA * （BLOCK_SIZE * by）;

wA 是A矩阵的宽度，也就是一行有多少个元素，BLOCK_SIZE * by是当前block从第几行开始，所以aBegin就是当前block的最开始的位置。
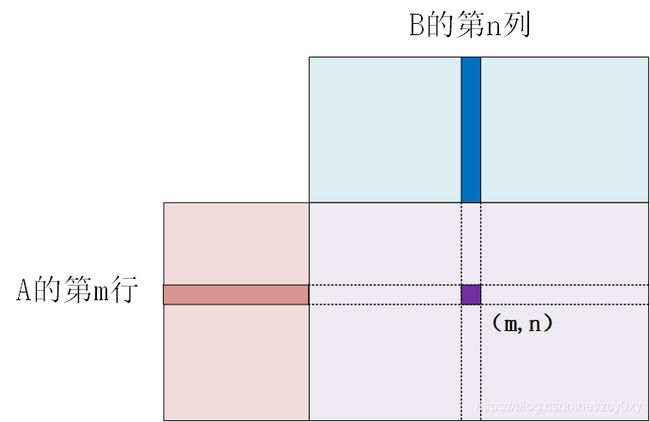
其他的4个参数看起来有点绕，不过想想也能知道分别代表什么。下面是直观的图，展示了几个参数分别代表什么位置。

图中的深红色方块和蓝色方块就是for里一个循环的计算量了。整个for走完一遍，就在A矩阵中从左走到右，B中从上走到下，对应的就是C中一个紫色方块的结果了。
下面详细到for里一个循环来看看每个线程干了什么。

    for (int a = aBegin, b = bBegin;
         a <= aEnd;
         a += aStep, b += bStep)
    {

		//共享内存，线程访问起来更快，同一个block共享同一个block
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
        As[ty][tx] = A[a + wA * ty + tx];
        Bs[ty][tx] = B[b + wB * ty + tx];

        //同步，等待同一个block的所有线程都完成了上一步，才会继续
		//因为必须保证数据都复制到As，Bs里去了才能操作计算他们
        __syncthreads();

        // #pragma unroll 这个语法就是把for循环在编译时手动展开
		//如果for循环次数比较少，可以这么做加快速度
#pragma unroll
        for (int k = 0; k < BLOCK_SIZE; ++k)
        {
            Csub += As[ty][k] * Bs[k][tx];
        }

        __syncthreads();
    }

    int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
    C[c + wB * ty + tx] = Csub;

画一个非常详细的图，就是下面这样：

想来这么看，就很清晰了，这份代码为了准确速度，做了很多工作。为了保证内存连续读取，每次读取的间隔是16的倍数啊等等，结果代码比较难搞懂。
这几个图使用visio画的，希望把逻辑讲清楚了。

扩展：matrixMulCUBLAS

matrixMulCUBLAS这个例程是调用了cuda自带的cuBLAS库来计算矩阵相乘的结果，关于这个库以及cublasSgemm()这个函数，我参考官方手册写了一篇介绍cuBLAS简介。
这个例程中的A、B矩阵都是随机初始化的，看不出是按照列优先排列的。

// Allocates a matrix with random float entries.
void randomInit(float *data, int size)
{
    for (int i = 0; i < size; ++i)
        data[i] = rand() / (float)RAND_MAX;
}

调用库函数，这个函数在cuBLAS简介作了介绍，计算结果存储在d_C，依然是列优先存储的格式：

        checkCudaErrors(cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, matrix_size.uiWB, 
        matrix_size.uiHA, matrix_size.uiWA, &alpha, d_B, matrix_size.uiWB,
         d_A, matrix_size.uiWA, &beta, d_C, matrix_size.uiWB));

算完以后，用CPU算了一遍，为了等会检查GPU计算的精度：

matrixMulCPU(float *C, const float *A, const float *B, unsigned int hA, 
unsigned int wA, unsigned int wB)
{
	//先遍历A的行，再遍历B的列
    for (unsigned int i = 0; i < hA; ++i)
        for (unsigned int j = 0; j < wB; ++j)
        {
            double sum = 0;

            for (unsigned int k = 0; k < wA; ++k)
            {
                double a = A[i * wA + k];
                double b = B[k * wB + j];
                sum += a * b;
            }

            C[i * wB + j] = (float)sum;
        }
}

结果比较

用“matrixMul”跑出来的

库函数的：

1334 GFlop/s对比3666 GFlop/s，库函数快了3倍, GFlop/s是十亿次浮点数运算/秒。
这个故事告诉我们，还是直接调用库函数方便，没事别瞎几把研究源码。