HNSW算法原理（一）

 

原文链接：https://blog.csdn.net/CHIERYU/article/details/81989920

HNSW算法可类比于skip lists数据结构，对于增和查操作，其与skip lists有很多相同之处，下面讲讲HNSW算法中的2个关键问题，即：如何确定待插入点的层次，如何调参。

一、HSNW算法将样本插入到第几层

每个样本属于哪个层呢？

首先要写一个确定层次的函数，样本点属于每一层的概率是确定好的，且是从底层到高层逐渐递减的。

确定每层概率的函数如下：

//from faiss code
//levelMult = 1/log(M)
void HNSW::set_default_probas(int M, float levelMult)
{
    int nn = 0; 
    cum_nneighbor_per_level.push_back (0); 
    for (int level = 0; ;level++) {
        float proba = exp(-level / levelMult) * (1 - exp(-1 / levelMult));
        if (proba < 1e-9) break;
        assign_probas.push_back(proba);
        nn += level == 0 ? M * 2 : M;//特别地，第0层要求2M个邻居，以提高recall
        cum_nneighbor_per_level.push_back (nn);
    }
}

上述代码的原理可以参考如下图片内容来辅助理解，层次t越大，那么概率应该越小。

确定样本层次的函数如下： 

//from faiss code
int HNSW::random_level()
{
    double f = rng.rand_float();
    // could be a bit faster with bissection
    for (int level = 0; level < assign_probas.size(); level++) {
        if (f < assign_probas[level]) {
            return level;
        }    
        f -= assign_probas[level];
    }    
    // happens with exponentially low probability
    return assign_probas.size() - 1; 
}

然后确定n个样本，每个样本的层次，它跟特征无关。

//from faiss code
for (int i = 0; i < n; i++) {
    int pt_level = hnsw.random_level();
    hnsw.levels.push_back(pt_level + 1);
}

int max_level = 0;
for (int i = 0; i < n; i++) {
    int pt_level = hnsw.levels[i + n0] - 1;
    if (pt_level > max_level) max_level = pt_level;
    hnsw.offsets.push_back(hnsw.offsets.back() + cum_nneighbor_per_level[pt_level + 1]);
    hnsw.neighbors.resize(hnsw.offsets.back(), -1);
}

上面的代码来自faiss，下面看看 hnswlib上是如何确定样本的层次的。

//from nmslib code
//c++11随机数产生器
std::default_random_engine level_generator_;
size_t random_seed = 100
level_generator_.seed(random_seed);

int getRandomLevel(double reverse_size) {
	//产生U(0,1)的随机数x,那么1-x也是均匀分布，-log(1-x)就是指数分布
	std::uniform_real_distribution distribution(0.0, 1.0);
	//逆变换采样？
	double r = -log(distribution(level_generator_)) * reverse_size;
	return (int) r;
}

//调用
size_t M_ = 16
mult_ = 1 / log(1.0 * M_);// 0.83048202372
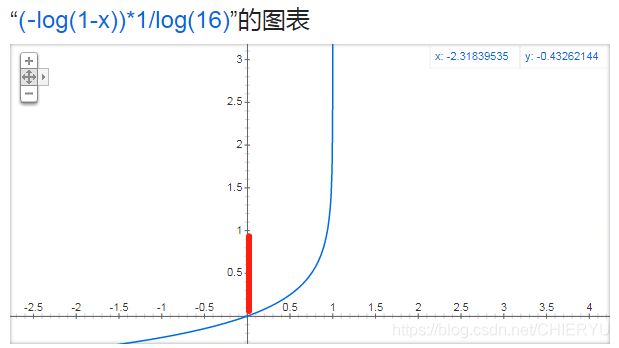
int curlevel = getRandomLevel(mult_);

下图中，横坐标表示概率，取值范围在[0,1]区间，对应蓝色的线往横坐标投影值；纵坐标表示某个点所在的最高层次，取值从0到正无穷，对应蓝色的线往纵坐标投影值。从中可以看到一个点对应的最高层次很大概率是第0层：

getRandomLevel函数结果与随机数对应关系

 

再看看Online-hnsw中是如何确定样本的层次的：

//from online-hnsw code
//https://github.com/andrusha97/online-hnsw/blob/master/include/hnsw/index.hpp
size_t random_level() {
	// I avoid use of uniform_real_distribution to control how many times random() is called.
	// This makes inserts reproducible across standard libraries.

	// NOTE: This works correctly for standard random engines because their value_type is required to be unsigned.
	auto sample = random() - random_t::min();
	auto max_rand = random_t::max() - random_t::min();

	// If max_rand is too large, decrease it so that it can be represented by double.
	//此处保证max_rand在[0,2^20]之间
	if (max_rand > 1048576) {
		sample /= max_rand / 1048576;
		max_rand /= max_rand / 1048576;
	}

	double x = std::min(1.0, std::max(0.0, double(sample) / double(max_rand)));
	//注意此处系数与hnswlib不同，第0层的是1/log(2M_+1),非0层是1/log(M_+1)
	return static_cast(-std::log(x) / std::log(double(options.max_links + 1)));
}

这样就预先设置了每层有多少样本点，当使用时：

//from faiss code
// build histogram
for (int i = 0; i < n; i++) {
    storage_idx_t pt_id = i + n0;
    int pt_level = hnsw.levels[pt_id] - 1;
    while (pt_level >= hist.size())
        hist.push_back(0);
    hist[pt_level] ++;
}

// accumulate
std::vector offsets(hist.size() + 1, 0);
for (int i = 0; i < hist.size() - 1; i++) {
    offsets[i + 1] = offsets[i] + hist[i];
}

每个段的元素数目确定了，那每个段是哪些元素呢？这是由hnsw.random_level()随机确定的。

//from faiss code
// bucket sort
for (int i = 0; i < n; i++) {
    storage_idx_t pt_id = i + n0;
    int pt_level = hnsw.levels[pt_id] - 1;
    order[offsets[pt_level]++] = pt_id;
}

至此，HNSW的插入样本的层次就确定了。

具体添加元素是怎么操作的呢？

调用函数add_with_locks。

二、HNSW的算法性能影响因素

HNSW算法需要调节的参数有哪些：M，efConstruction，levelMult，M_max0

为了获得最佳的性能，那么要求不同层的邻居点之间的重叠要小，为了降低重叠，那么就要降低levelMult，但是会使得每层的hop的个数增加，从而降低速度。在低位数据上调节好的参数到高维空间中很难成立，It is hard to expect the same behavior for high dimensional data since in this case the k-NN graph already has very short greedy algorithm paths.  但是在高维空间增加levelMult会让速度更快却没有负面效果。但是对于128维来说还是有影响的。

Further increase(>100 in a 10M SIFT dataset) of the efConstruction leads to little extra performance but in exchange of significantly longer construction time.

在遍历的过程中，traverse the graph,从1度邻居点，到2度邻居点，不断往外扩，扩的过程中将更近的点加入结果列表中。由于下一个点属于上层的概率为p=exp(-levelMult)，因此在搜索该节点的邻居时是有概率为p的可能性到此为止的，代码中bool visisted来标记是否访问过（想想看如何做并行访问）。

 

想要了解更多关于faiss的线程问题，可以参考：http://houjie13.com/articles/2018/06/25/1529933223485.html

本文原文链接：https://blog.csdn.net/CHIERYU/article/details/81989920