并查集原理、代码、例题演示

并查集

原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)

比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。（-1代表初始的小集体中只有自己一个）

毕业后，学生们要去公司上班，每个地方的学生自发组织成小分队一起上路，于是：西安学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}就相互认识了，10个人形成了三个小团体。假设右三个群主0,1,2担任队长，负责大家的出行。

一趟火车之旅后，每个小分队成员就互相熟悉，称为了一个朋友圈

从上图可以看出：编号6,7,8同学属于0号小分队，该小分队中有4人(包含队长0)；

编号为4和9的同学属于1号小分队，该小分队有3人(包含队长1)，编号为3和5的同学属于2号小分队，该小分队有3个人(包含队长1)。
仔细观察数组中内融化，可以得出以下结论：

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标

在公司工作一段时间后，西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起，两个小圈子的学生相互介绍，最后成为了一个小圈子：

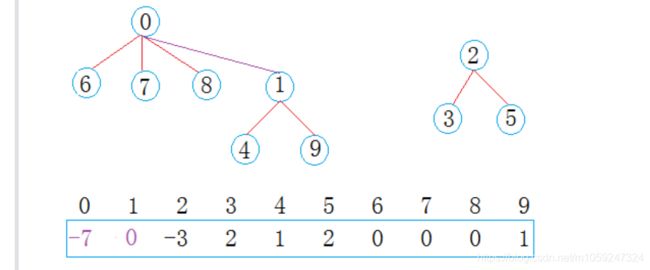
现在0集合有7个人，2集合有3个人，总共两个朋友圈。
通过以上例子可知，并查集一般可以解决一下问题：

1. 查找元素属于哪个集合
   沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
   沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
3. 将两个集合归并成一个集合
   将两个集合中的元素合并
   将一个集合名称改成另一个集合的名称
4. 集合的个数
   遍历数组，数组中元素为负数的个数即为集合的个数。

代码实现

class UnionSet
{
     
public:
	//初始值都置-1，代表团体只有自己一个
	UnionSet(size_t n)
	{
     
		_v.resize(n, -1);
	}
	 // 给一个元素的编号，找到该元素所在集合的名称
	int FindRoot(int x)
	{
     
		// 如果数组中存储的是负数，找到，否则一直继续
		while (_v[x] >= 0)
			x = _v[x];
		return x;
	}

	bool Union(int x1, int x2)
	{
     
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		if (root1 == root2) return false;

		//二者没在同一个集合，就进行合并，谁做根都可以

		_v[root1] += _v[root2];
		_v[root2] = root1;
        
        return true;
	}
	// 数组中负数的个数，即为集合的个数
	size_t Size()
	{
     
       int n = 0;
		for(auto e : _v)
        {
     
            if(e < 0)
                ++n;
        }
        return n;
	}

private:
	vector<int> _v;
};

LeetCode经典例题

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

输入: [[1,1,0], [1,1,0], [0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。第2个学生自己在一个朋友圈。所以返回2。

输入:
[[1,1,0],[1,1,1],[0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/friend-circles

class UnionSet
{
     
public:

	UnionSet(size_t n)
	{
     
		_v.resize(n, -1);
	}

	int FindRoot(int x)
	{
     
		while (_v[x] >= 0)
			x = _v[x];
		return x;
	}

	bool Union(int x1, int x2)
	{
     
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		if (root1 == root2) return false;

		_v[root1] += _v[root2];
		_v[root2] = root1;
        
        return true;
	}

	size_t Size()
	{
     
       int n = 0;
		for(auto e : _v)
        {
     
            if(e < 0)
                ++n;
        }
        return n;
	}

private:
	vector<int> _v;
};
class Solution {
     
public:
    int findCircleNum(vector<vector<int>>& M)
    {
     
        UnionSet us(M.size());
        
        for(int i = 0; i < M.size(); ++i)
        {
     
            for(int j = 0; j < M[i].size(); ++j)
            {
     
                if(M[i][j] == 1)   //只要二者存在联系，就并入一个团体
                    us.Union(i,j);
            }
        }
        return us.Size();
    }
};