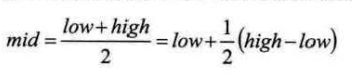数据结构与算法(十二)二分查找和插值查找

1、二分查找

有一个游戏最能体现二分查找的思路：我在纸上已经写好了100以内的正整数数字，然后请你猜，问最多几次可以猜出来？

这个游戏的解法就是每次猜数后折取一半，我们把这种每次取中间记录查找的方法叫做折半查找，或二分查找。

二分查找(Binary earch)，也称为折半查找。它的前提是线性表中的记录必须是关键码有序(通常从小到大有序) ，线性表必须采用顺序存储。

二分查找的基本思想是：

• 在有序表中，取中间数据作为比较对象，若给定值与中间记录的关键字相等，则查找成功；
• 若给定值小于中间记录的关键字，则在中阔记录的左半区继续查找；
• 若给定值大于中间记录的关键字，则在中间记录的右半区继续查找；
• 不断重复上述过程，直到查找成功，或所有查找区域元记录，查找失败为止。

/*二分查找算法*/
int BinarySearch(int *a, int length, int key)
{
	/*数组从1开始，0保留为查找失败*/
    int low  = 1;      /*定义最小下标为记录首位*/
    int high = length; /*定义最大下标为记录末位*/
    int mid;
    while (low <= high) 
    {     
        mid = (low+high)/2;   /*折半，mid为中间数据*/
        if (keya[mid]) /*若查找值比mid值大*/
            low = mid+1;     /*最小下标变为现在mid下标后一位，继续查找*/
        else 
            return mid;      /*相等说明找到，返回mid*/
    }
    return 0;
}

该算法还是比较容易理解的，同时我们也能感觉到它的效率非常高。但到底高多少？关键在于算法的时阅复杂度分析。

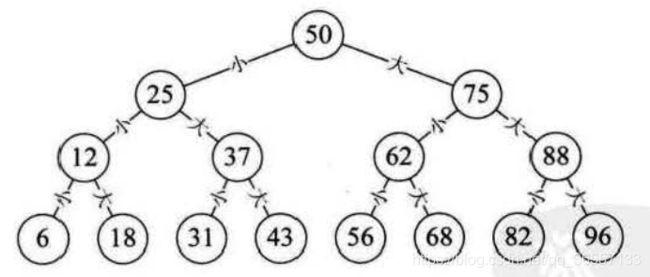
从上面的二叉树可以看出，二分查找的最坏情况就是查找到二叉树的叶子结点，查找次数等于二叉树的深度㏒₂n+1，所以算法时间复杂度为O(㏒₂n) 与，它显然远远好于顺序查找的O(n)时间复杂度了。数据量越大O(㏒₂n)的效率就越优于O(n)。

不过由于二分查找的前提条件是需要有序顺序表来存储，且不能用链表作存储结构，对于静态查找表，一次排序后不再变化，这样的算法已经非常好了。

但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序就会带来不小的开销，那就不建议使用。

没有bug的二分查找：

现在请问，上面的二分查找代码有没有问题？哪段代码会出现 bug ？

对于上面这段代码而言，问题出在：mid = (low + high) / 2。

这句代码在 low 和 high 很大的时候，low + high可能会出现大于INT_MAX的溢出的情况，从而导致数组下标访问错误。

 一般的做法是将加法变成减法：mid =  low + (high - low) / 2。 

还有一种更高逼格的写法，也是官方的二分查找的写法，使用位运算：mid =  low + ((high - low) >> 1)。

使用位运算优化乘、除以及模运算

2、插值查找

我们可以在二分查找的基础上思考，为什么一定要折一半，而不是折四分之一或者折更多呢？

例如之前提到的斐波那契查找就是按照黄金分割比例进行对折，那么如何折才是最优的？

打个比方，在英文词典里查“apple”，你下意识里翻开词典是翻前面的书页，还是后面的书页呢？

如果再让你查 “zoom”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的直接翻前面或后面。

同理，取值范围0~10000之间的100个元素从小到大均匀分布在数组中，如果我们需要查找5，我们自然会考虑从数组下标较小的开始查找，而如果我们需要查找8000，那自然从数组下标较大的开始查找。

我们先对二分查找的计算中值公式进行变换，这样mid就等于low加上high和low的差的一半：

我们考虑将1/2这个系数进行改进，下面为改进方案：

key-a[low]是为了得到查找值比最小值大多少，a[high]-a[low]得到这个有序序列的均匀分布情况，(key-a[low]) / (a[high]-a[low])就可以得到查找值在这个均匀分布的有序序列中的大致位置的系数，而改进后的查找方法称为插值查找，其核心就在于插值的计算公式。

现在有一个有序序列a = {0,1,16,24,35,47,59,62,73,88,99}（在0~100之间均匀分布），我们需要查找key=59，length=10，如果使用斐波那契查找就需要查找4次，如果使用二分查找那么需要查找3次。

如果使用插值查找，第一次：(key-a[low]) / (a[high]-a[low]) = (59-1)/(99-1) = 58/98 = 0.592，mid=low+(high-low)*0.592 = 1+9×0.592 = 6.92 ≈ 6，而a[mid=6] = 59，只查找1次就找到了。相比斐波那契查找和二分查找，此时的插值查找的效率明显提高了很多。

虽然这三种查找方法的时间复杂度都为O(㏒₂n)，但可以看出，在分布均匀且表较长的查找表来说，插值查找的效率要好太多。但反之查找表类似{1, 2, 3, 2000, 2001, 10000, ......}这样极端不均匀的数据而言，插值查找的效率就不如斐波那契查找和二分查找，插值查找就不是很合适的选择。

/*插值查找算法*/
int BinarySearch(int *a, int length, int key)
{
	                  /*数组从1开始，0保留为查找失败*/
    int low = 1;      /*定义最小下标为记录首位*/
    int high = length; /*定义最大下标为记录末位*/
    int mid;
    while (low <= high) 
    {     
        mid = low+(high-low)*(key-a[low])/(a[high]-a[low]);/*插值计算公式*/
        if (keya[mid]) /*若查找值比mid值大*/
            low = mid+1;     /*最小下标变为现在mid下标后一位，继续查找*/
        else 
            return mid;      /*相等说明找到，返回mid*/
    }
    return 0;
}

注：还有关键的一点，二分查找进行的是简单的加法和除法运算，斐波那契查找进行的是最简单的加减法运算，而插值查找进行相当复杂的加减乘除都有的四则运算，如果在海量的数据查找中，这种细微的差别可能也会影响最终的查找效率，所以使用哪种查找方法还是需要视情况进行比较后来选择。