数据分析面试题——统计理论

1. 扑克牌54张，平均分成2份，求这2份都有2张A的概率。
解：
排列公式 ：$A_n^m=n(n-1)(n-1)...(n-m+1)=\frac{n!}{(n-m)!}$
组合公式：$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)...(n-m+1)}{m(m-1)...1}=\frac{n!}{m!(n-m)!}$
将扑克牌分成两堆，每堆27张。
分母：先选27张，剩下27张自成一堆，$C_{54}^{27}$
分子：一共4张A，先从4张A中选2张（无序）$C_4^2$，再从50张（非A）中选25张$C_{50}^{25}$
$$P=\frac{C_4^2{C}_{50}^{25}}{C_{54}^{27}}$$
2. 男生点击率增加，女生点击率增加，总体为何减少?
解：
因为男女的点击率可能有较大差异，同时低点击率群体的占比增大。
如原来男性20人，点击1人；女性100人，点击99人，总点击率100/120。
现在男性100人，点击6人；女性20人，点击20人，总点击率26/120。
3. 参数估计
参数估计：是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。

例如，$X\sim N(\mu ,{\sigma }^2)$，若$\mu ,\sigma$未知，通过构造样本的函数，给出它们的估计值（点估计）或取值范围（区间估计）就是参数估计的主要任务。

点估计：依据样本估计总体分布中所含的未知参数或未知参数的函数。
区间估计（置信区间的估计）：依据抽取的样本，根据一定的正确度与精确度的要求，构造出适当的区间，作为总体分布的未知参数或参数的函数的真值所在范围的估计。例如人们常说的有百分之多少的把握保证某值在某个范围内，即是区间估计的最简单的应用。



（1） 矩估计
思想：矩估计是基于一种简单的“替换”思想，即用样本矩估计总体矩。
理论：矩估计的理论依据就是基于大数定律的，大数定律语言化表述为：当总体的k阶矩存在时，样本的k阶矩依概率收敛于总体的k阶矩，即当抽取的样本数量n充分大的时候，样本矩将约等于总体矩。
定义：令k为正整数或0，a为任意实数，X为随机变量。则期望值$E(x-a{)}^k$叫做随机变量X对a的k阶矩。如果有a=0，则$E(x{)}^k$叫做k阶原点矩，也叫k阶矩。
计算：
样本k阶原点矩$A_k=\frac{1}{n}{\sum }_{i=1}^n{X}_i^k$ ==> >总体k阶原点矩${\mu }_k=E(X^k)$
样本k阶中心矩$B_k=\frac{1}{n}{\sum }_{i=1}^n(X_i-\bar{X}{)}^k$ ==> >总体k阶中心矩$m_k=E([X-E(X){]}^K)$
即令样本k阶矩与总体k阶矩相等
例子

优点：简单易行，不需要事先知道总体是什么分布。（仅需按照均值和方差计算即可）。
缺点：总体类型已知时，未充分利用提供的分布信息，有些情况下，矩估计的量不唯一（样本矩近似总体矩有一定的随意性）。
（2） 极大似然估计
似然函数：似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。“似然性”与”概率”意思相近，都是指某种事件发生的可能性。概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。在这种意义上，似然函数可以理解为条件概率的逆反。在已知某个参数B时，事件A会发生的概率写作$P(A|B)=\frac{P(A,B)}{P(B)}$
极大似然估计的目的：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
原理：极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。
求解：
记已知一个独立同分布的样本集为$D{X}_1,X_2,..,X_n$，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为$F_d$，以及一个分布参数$\theta$
$$P\{X_1,X_2,..,X_n\}=F_d\{X_1,X_2,..,X_n|\theta \}$$
似然函数：$L(\theta )=P{X}_1,X_2,...,X_n={\prod }_{i=1}^{n}P(X_i|\theta )$
$$\hat{\theta }=argma{x}_{\theta }L(\theta )$$
$\hat{\theta }$是参数空间中能使似然函数最大的θ值，则应该是“最可能”的参数值
一般取对数似然，对$\theta$求偏导令其为0得到 $\hat{\theta }$得值。
优缺点
a.比其他估计方法更加简单；
b.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；
c.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。

4. 假设检验
参数估计和假设检验是统计推断的两个组成部分，它们都是利用样本对总体进行某种推断，但推断的角度不同。
参数估计讨论的是用样本估计总体参数的方法，总体参数μ在估计前是未知的。
而在假设检验中，则是先对μ的值提出一个假设，然后利用样本信息去检验这个假设是否成立。
https://blog.csdn.net/csefrfvdv/article/details/100705856(假设检验的例子)
p值就是对于观察到的数据，能获得的拒绝H0的最小的显著性水平$\alpha$。也可以简单说成是错误地拒绝了 H0 的概率。也就是Type 1 Error。

5. 置信度、置信区间
置信区间是我们所计算出的变量存在的范围（误差范围），置信水平就是我们对于这个数值存在于我们计算出的这个范围的可信程度。
“我们有95%的信心认为眼前这个样本统计值（可以是平均值、回归系数或净回归系数）的置信区间包含总体参数”，意思是：如果我们采用同一个抽样程序，从一个总体中抽到样本量相同的无数个样本，每个样本中得到一个样本统计值，每个样本统计值有一个置信区间，假设这无数个置信区间是百分之百，那么其中95%包括总体参数，我们有95%的信心认为眼前这个置信区间包括总体参数，也就是说，我们有95%的信心认为眼前这个置信区间包括总体参数是那95%中的一个。
计算“置信区间”是应用性研究，是做完显著度检验之后的跟进分析。显著度检验告诉我们能在什么信心度上放弃零假设。显著度检验中的“p值”是以正话反说的方式表示信心度。例如，p=0.05，意思是信心度为95%，亦即“放弃了零假设，但只冒了5%的犯一类错误的风险”。

• 已知总体方差，求总体均值的置信区间
  
• 未知总体方差，求总体均值的置信区间：

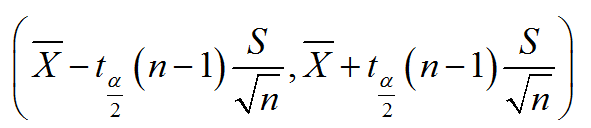
6. 协方差与相关系数的区别和联系
协方差：
协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

相关系数：
研究变量之间线性相关程度的量，取值范围是[-1,1]。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

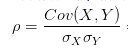
就是用X、Y的协方差除以X的标准差和Y的标准差。

可以看出$X-{\mu }_x$是偏离均值的幅度，取平方是为了消除负号，避免正负抵消。最后求平均值才能更好的体现每次变化偏离均值的情况。
既然是一种特殊的协方差：
1）也可以反映两个变量变化的是同向还是反向的，如果同向就为正，反向就为负。
2）由于它是标准化后的协方差，它消除了两个变量变化幅度的影响，而只是单纯反映两个变量每单位变化时的相似程度。

7. 中心极限定理 & 大数定律
中心极限定理定义：
（1）任何一个样本的平均值将会约等于其所在总体的平均值。
（2）中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。

一般来说，n个独立同分布的随机变量的和的分布函数是比较难求的，而通过中心极限定理，可以描述当n足够大的时候，这些随机变量的和的分布近似服从正态分布。下面主要讲述两条中心极限定理的

独立同分布的中心极限定理 ：随机变量 $X_1,X_2,\dots X_n$ 独立同分布，且具有数学期望$E(X_k)=\mu$, 和方差 $D(X_k)={\sigma }^2>0(k=1,2,3\dots )$, 则随机变量之和 ${\sum }_{k=1}^n{X}_k$ 的标准化变量
$$Y_n=\frac{{\sum }_{k=1}^n{X}_k-E({\sum }_{k=1}^n{X}_k)}{\sqrt{D({\sum }_{k=1}^n{X}_k)}}=\frac{{\sum }_{k=1}^n{X}_k-n\mu }{\sqrt{n}\sigma }$$的分布函数 $F_n(x)$ 对于任意 $x$ 满足
$$\underset{n\to \infty }{\lim }{F}_n(x)=\underset{n\to \infty }{\lim }P(\frac{{\sum }_{k=1}^n{X}_k-n\mu }{\sqrt{n}\sigma }\le x)={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}{e}^{-t^2/2}dt$$
当上面的 $n$ 充分大的时候，$\frac{{\sum }_{k=1}^n{X}_k-n\mu }{\sqrt{n}\sigma }$ 服从正态分布 $N(0,1)$
也可以将上面分布写成下面的形式

$\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}$~$N(0,1)$ 或 $\overline{X}$~$N(\mu ,{\sigma }^2/n)$

也就是说，当样本的数量n足够大的时候，样本均值服从均值为 $\mu$, 方差为 ${\sigma }^2/n$ 的正态分布， 其中 $\mu$ 和 $\sigma$ 分别是原来随机变量的所服从的分布的期望和方差，这一结果是数理统计中大样本统计推断的基础。
上面的独立同分布中每个随机变量都是同分布的，也就是具有同样的期望和方差，那么如果随机变量的分布独立呢？下面是对应这种情况的中心极限定理。
李雅普诺夫定理 设随机变量 $X_1,X_2,\dots X_n$ 相互独立，具有数学期望和方差$$E(X_k)={\mu }_k,D(X_k)={\sigma }_k^2>0,k=1,2,\dots$$,记$$B_n^2=\sum _{k=1}^n{\sigma }_k^2$$ 若存在正数 $\delta$, 使得当 $n\to \infty$ 时，$$\frac{1}{B_n^{2+\delta }}\sum _{k=1}^{n}E(|X_k-{\mu }_k{|}^{2+\delta })\to 0$$
定义随机变量 $Z_n$ 为$$Z_n=\frac{{\sum }_{k=1}^n{X}_k-{\sum }_{k=1}^n{\mu }_k}{B_n}$$
那么当n很大时,只要满足定理中的条件，那么随机变量 $Z_n$ 服从正态分布 $N(0,1)$。
tips:
a) 总体本身的分布不要求正态分布
b) 样本每组要足够大，但也不需要太大，取样本的时候，一般认为，每组大于等于30个，即可让中心极限定理发挥作用。
中心极限定理作用：
（1）在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体。
（2）根据总体的平均值和标准差，判断某个样本是否属于总体。

大数定律
大数定律有弱大数定律和强大数定律，两者描述的都是样本数量越多，则其平均就越趋近期望值。两个简单的区别就是弱大数定律表示样本均值依概率收敛于总体均值，而强大数定律表示了样本均值可以以概率为1收敛于总体均值。
弱大数定理（辛钦大数定理） 设 $X_1,X_2,\dots$ 是独立同分布的随机变量序列，且具有数学期望 $E(X_k)=\mu (k=1,2,,\dots .)$,取前 n 个变量的算术平均 $\frac{1}{n}{\sum }_{k=1}^n{X}_k$, 对于任意的 $ϵ$,有
$$\underset{n\to \infty }{\lim }P(|\frac{1}{n}\sum _{k=1}^n{X}_k-\mu |<ϵ)=1$$
定义描述的就是当样本数n足够大时，样本均值与总体期望的差可以无限小，也就是可以通过样本均值估计总体期望。
伯努利大数定理 设 $f_A$ 是 n 次独立重复试验中事件 $A$ 发生的次数，$p$ 是事件 $A$ 在每次试验中发生的概率，则对于任意正数 $ϵ>0$, 有$$\underset{n\to \infty }{\lim }P(|\frac{f_A}{n}-p|<ϵ)=1$$或$$\underset{n\to \infty }{\lim }P(|\frac{f_A}{n}-p|\ge ϵ)=0$$
伯努利大数定理主要描述当样本数足够大时，可以用样本的频率来估计总体的概率，其本质跟辛钦弱大数定理是一样的。

大数定理（LLN）和中心极限定理（CLT）的联系与区别
共同点：都是用来描述独立同分布（i.i.d）的随机变量的和的渐进表现（asymptotic behavior)
区别：首先，它们描述的是在不同的收敛速率（convergence rate）(差了个$\sqrt{n}$)之下的表现，其次LLN前提条件弱一点：$E(|X|)\le \infty$ , CLT成立条件强一点：$E(X^2)\le \infty$

8. P值的含义
使用P值的原因：置信水平（如0.05）是一个通用的风险概率，这是用域表示的缺陷，但根据不同的样本结果进行决策，面临的风险事实上是有差别的，为了精确地反应决策的风险度，这时就需要利用p值来判断哪一个样本计算的统计量更精确。
P值的定义：p值是指当原假设为真时样本观察结果或更极端结果出现的概率。如果p值很小，说明这种情况发生的概率很小，如果这种情况出现了，根据小概率原理，我们就有理由拒绝原假设1，p值越小，拒绝原假设的理由就越充分。
p值的优点：它反映了观察到的实际数据与原假设之间不一致的概率，与传统的拒绝域范围相比，p值是一个具体的值，这样就提供了更多的信息。
通过p值让我们可以更准确的做出决策。也可以直接使用p值进行决策，这时p值本身就代表了显著性水平。也可以使用p值，按照所需要的显著性水平进行判断和决策，具体做法就是将p值和需要的显著性水平进行比较。
P值计算：
左侧检验的P值为检验统计量X 小于样本统计值C 的概率，即：P = P{ X < C}
右侧检验的P值为检验统计量X 大于样本统计值C 的概率：P = P{ X > C}双侧检验的P值为检验统计量X 落在样本统计值C 为端点的尾部区域内的概率的2 倍：P = 2P{ X > C} (当C位于分布曲线的右端时) 或P = 2P{ X< C} (当C 位于分布曲线的左端时) 。
计算出P值后，将给定的显著性水平α与P 值比较，就可作出检验的结论：
如果P<α值，则在显著性水平α下拒绝原假设。
如果P≥α值，则在显著性水平α下接受原假设。

9.时间序列分析
是同一现象在不同时间上的相继观察值排列而成的序列。

10.怎么向小孩子解释正态分布

拿出小朋友班级的成绩表，每隔2分统计一下人数（因为小学一年级大家成绩很接近），画出钟形。然后说这就是正态分布，大多数的人都集中在中间，只有少数特别好和不够好
拿出隔壁班的成绩表，让小朋友自己画画看，发现也是这样的现象
然后拿出班级的身高表，发现也是这个样子的
大部分人之间是没有太大差别的，只有少数人特别好和不够好，这是生活里普遍看到的现象，这就是正态分布

11、 下面对于“预测变量间可能存在较严重的多重共线性”的论述中错误的是？
A. 回归系数的符号与专家经验知识不符（对）
B. 方差膨胀因子（VIF）<5（错，大于10认为有严重多重共线性）
C. 其中两个预测变量的相关系数>=0.85（对）
D. 变量重要性与专家经验严重违背（对）
当解释变量之间存在一定程度的相关性（近似共线性）时，也可以称之为多重共线性。当有多重共线性的情况发生时，参数估计的结果不再具有有效性，因此在进行逻辑回归分析之前我们需要通过VIF检验来排除掉某些有多重共线性的变量。
VIF指的是解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比，可以反映多重共线性导致的方差的增加程度。
$$VIF=\frac{1}{1-R^2}$$
R2是线性回归中的决定系数，反映了回归方程解释因变量变化的百分比。
它可以由因变量和自变量之间的复相关系数的平方得到，也可以由回归方程的残差平方和和总平方和的比值得到。为了得到每一个变量的VIF，我们需要以每一个变量为因变量对其余所有变量进行线性回归分析，对每一个变量得到各自的R2，再代入上面的式子，就可以得到每一个变量的VIF了。
复相关系数是反映一个因变量与一组自变量(两个或两个以上)之间相关程度的指标，其实就是因变量和自变量拟合结果之间的相关系数。($\widehat{X1}=0.0572X2+1.5178X3-3.8466$,就是预测的$\widehat{X1}$和X1的相关系数$R^2=r(X1,\widehat{X1}{)}^2=0.9398$)
回归平方和：$SSR={\sum }_{i=1}^n(\widehat{y_i}-\overline{y}{)}^2$
残差平方和：$SSE={\sum }_{i=1}^n(y_i-\widehat{y_i}{)}^2$
总平方和：$SST={\sum }_{i=1}^n(y_i-\overline{y}{)}^2$ $SST=SSR+SSE$
$$R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$

12. PCA为什么要中心化？PCA的主成分是什么？
中心化是对每一个样本向量做的

• 所谓去中心化，就是将样本X中的每个观测值都减掉样本均值，这样做的好处是能够使得求解协方差矩阵变得更容易。
• PCA通常是用于高维数据的降维，它可以将原来高维的数据投影到某个低维的空间上并使得其方差尽量大。如果数据其中某一特征（矩阵的某一列）的数值特别大，那么它在整个误差计算的比重上就很大，那么可以想象在投影到低维空间之后，为了使低秩分解逼近原数据，整个投影会去努力逼近最大的那一个特征，而忽略数值比较小的特征。因为在建模前我们并不知道每个特征的重要性，这很可能导致了大量的信息缺失。为了“公平”起见，防止过分捕捉某些数值大的特征，我们会对每个特征先进行标准化处理，使得它们的大小都在相同的范围内，然后再进行PCA。
• 此外，从计算的角度讲，PCA前对数据标准化还有另外一个好处。因为PCA通常是数值近似分解，而非求特征值、奇异值得到解析解，所以当我们使用梯度下降等算法进行PCA的时候，我们最好先要对数据进行标准化，这是有利于梯度下降法的收敛。

13. 极大似然估计
利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。