R语言|回归分析(一) ———R语言数据分析系列(一)
回归分析
- 数据准备
-
- 数据基本信息
- 建立回归模型
-
- 建立回归方程
- 预测数值
- 回归方程可视化
-
- 散点图加拟合
- 回归方程诊断
- 完整代码
回归分析它是最为人熟知的建模技术之一。线性回归通常是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。【该分析完整代码附于文章末】
数据准备
首先加载“gcookbook”包,这个包包含由OReilly Media出版的Winston Chang所著的《R Graphics Cookbook》一书中使用的数据集。
数据基本信息
调用"gcookbook"数据包中的heightweight数据框。
#install.packages("gcookbook") #没有下载过的可先运行此语句
library(gcookbook) #引用gcookbook数据集
View(heightweight) #heightweight为下面分析所用数据
str(heightweight) #按例查看数据形式
summary(heightweight) #查看数据基本内容
先查看数据的变量,如图1,该数据框有236行5列,其中包含了性别、年龄、月数、身高、体重五个变量。除了性别,其余的都是数值型数据。
 图1 数据的变量信息 图1 数据的变量信息
|
接下来查看数据的基本内容,如图2,这些年龄为11岁到17岁的青少年,平均年龄为13岁,男女比例基本各占一半,男性(male)仅比女性(famale)多14人。
 图2 数据的基本内容 图2 数据的基本内容
|
建立回归模型
建立回归方程
直接调用系统lm()函数,下面将做结果解读。
model <- lm(heightIn~ageYear,heightweight) #建立回归模型
model #直接查看回归系数
summary(model) #查看回归模型参数
首先查看方程形式,直接查看回归系数,如图3,常数项系数为37.436,常数项系数为1.748,因此该回归方程表示为
y = 37.4 + 1.75 x y=37.4+1.75x y=37.4+1.75x
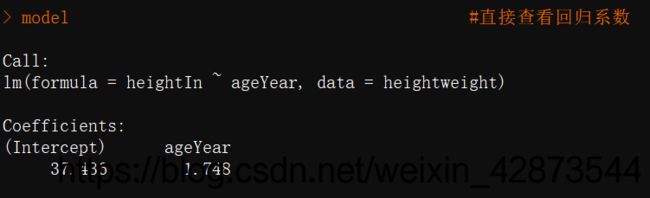 图3 回归方程的回归系数 图3 回归方程的回归系数
|
回归方程最主要还是看回归参数,如图4,可看出残差分析(Residuals)、系数项(Coefficients)、P值(p-value)、调整R方(Adjusted R-squared)均在下图对应位置。在系数分析一栏,每一项后面的星号代表着显著性的大小。图中显示R方为0.4225,P值为 p = 2.2 ∗ 1 0 − 16 p=2.2*10^{-16} p=2.2∗10−16。
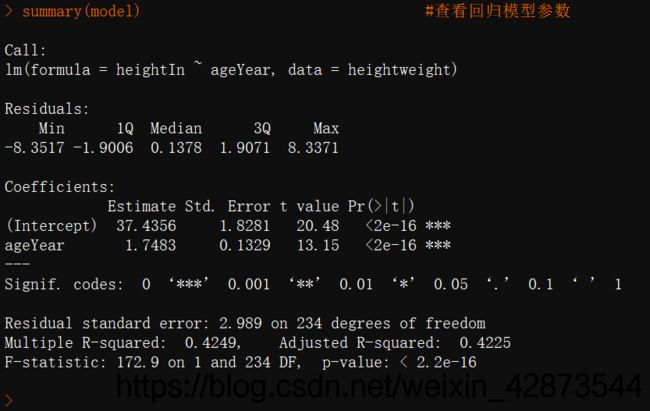 图4 回归方程的模型参数 图4 回归方程的模型参数
|
预测数值
首先建立需要预测的自变量数值,其次调用predict()函数进行预测。
data.frame()
xmin <- min(heightweight$ageYear)
xmax <- max(heightweight$ageYear)
predicted <- data.frame(ageYear = #创建需要预测的自变量数值
seq(xmin,xmax,length.out = 100))
predicted$heightIn <- predict(model,predicted) #预测数值
回归方程可视化
散点图加拟合
此处利用ggplot()函数进行可视化操作,分层次依次添加需要的东西。
ggplot(heightweight, aes(x=ageYear, y=heightIn,color="#5e616d"))+
geom_point()+ #绘画散点图
stat_smooth(method = lm,color="black")+ #在散点图加回归拟合线
annotate("text", label = "R^2==0.42",parse=T,x=16,y=52)+ #在图上添加R方
annotate("text", label = "y=37.4+1.75x",x=16,y=50) #在图上添加方程
如图5为散点图加以拟合图像。
 图5 回归方程可视化 图5 回归方程可视化
|
回归方程诊断
如图6左上,线性:若x与y线性相关,则残差和拟合应该没有任何系统关联,如果图上呈现出曲线,可能要考虑给方程加二次项。
如图6右上,正态性:当预测变量的值固定时,因变量成正态分布,因此残差也应该为均值为0的正态分布。Q-Q图是在正态分布对应的值下,标准化残差的概率图。若满足正态假设,则图上的点应落在图中的45度线上。若不是,则违反了正态分布的假设。
如图6左下,同方差性:若满足方差不变则图中的点应均匀分布在红色水平线两侧。
如图6右下,离群点、杠杆值、强影响点:在图中可以看到观测点217是个强影响点,依据是它距离cook’s distance 距离较远,因此删除它可以使得拟合效果更好。不过,删变量要尽量谨慎,不能一昧追求回归效果好而删原始值。
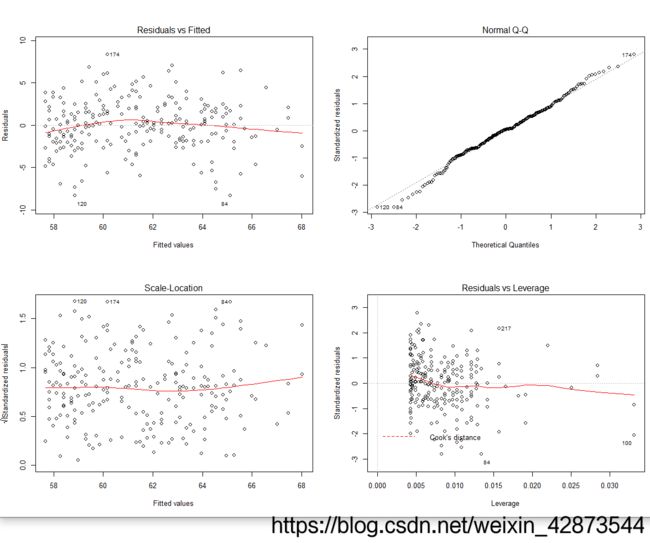 图6 回归方程诊断 图6 回归方程诊断
|
完整代码
#install.packages("gcookbook") #没有下载过的可先运行此语句
library(gcookbook) #引用gcookbook数据集
View(heightweight) #heightweight为下面分析所用数据
str(heightweight) #按例查看数据形式
summary(heightweight) #查看数据基本内容
model <- lm(heightIn~ageYear,heightweight) #建立回归模型
model #直接查看回归系数
summary(model) #查看回归模型参数
data.frame()
xmin <- min(heightweight$ageYear)
xmax <- max(heightweight$ageYear)
predicted <- data.frame(ageYear = #创建需要预测的自变量数值
seq(xmin,xmax,length.out = 100))
predicted$heightIn <- predict(model,predicted) #预测数值
ggplot(heightweight, aes(x=ageYear, y=heightIn,color="#5e616d"))+
geom_point()+ #绘画散点图
stat_smooth(method = lm,color="black")+ #在散点图加回归拟合线
annotate("text", label = "R^2==0.42",parse=T,x=16,y=52)+ #在图上添加R方
annotate("text", label = "y=37.4+1.75x",x=16,y=50) #在图上添加方程
par(mfrow=c(2,2)) #划分展示板
plot(model) #绘制诊断图像
1