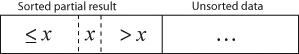排序算法之插入排序

一：概念

 

插入排序（英文为Insertion sort ）:  插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

 

二：原理

 

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

 

·         从第一个元素开始，该元素可以认为已经被排序

 

·         取出下一个元素，在已经排序的元素序列中从后向前扫描

 

·         如果该元素（已排序）大于新元素，将该元素移到下一位置

 

·         重复步骤3，直到找到已排序的元素小于或者等于新元素的位置

 

·         将新元素插入到该位置后

 

·         重复步骤2~5

 

如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找排序。

 

In-place 简单理解：排序通常是在原地。 k次迭代后得到的数组，其中第k +1项进行排序的属性。在每次迭代中对输入的所述第一剩余条目被删除，在正确的位置插入的结果，从而延长了结果：

 

排序前：

 

 

排序后：

 

 

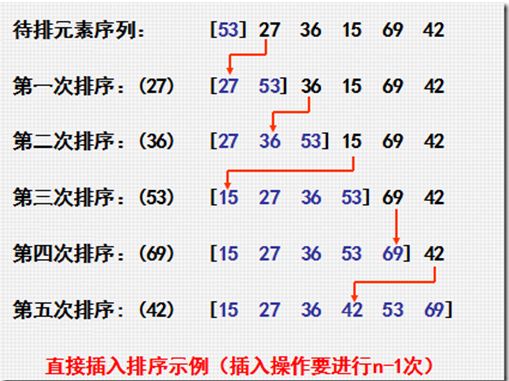
例子：流程图形式

 

 

 

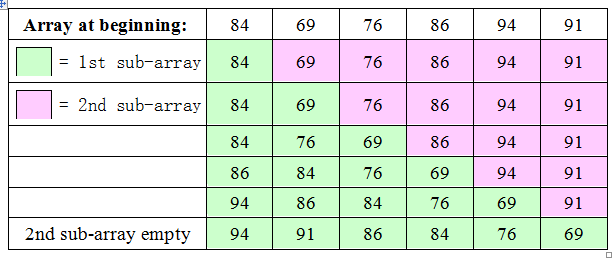
总上所述：插入排序是把数组分两个子数组，第一子数组（通常是左边的数组）是排过序的，第二个子数组是没有排序的。

 

 

 

三：特点

 

·         Simple implementation

 

·         Efficient for (quite) small data sets

 

·         Adaptive (i.e., efficient) for data sets that are already substantially sorted: the time complexity is O(n + d), where d is the number of inversions

 

·         More efficient in practice than most other simple quadratic (i.e., O(n²)) algorithms such as selection sort or bubble sort; the best case (nearly sorted input) is O(n)

 

·         Stable; i.e., does not change the relative order of elements with equal keys

 

·         In-place; i.e., only requires a constant amount O(1) of additional memory space

 

·         Online; i.e., can sort a list as it receives it

 

·         实现简单

 

·         对于小型数据集效率很高

 

·         自适应（即有效），为那些已经大幅排序的数据集：时间复杂度为O（N + D），其中d是反转的数目

 

·         在实践中更有效地比大多数其他简单的二次（即，O（N²））算法，如选择排序、冒泡排序；最好的情况下（近排序的输入）为O（N）

 

·         稳定性；即，不改变元素的相对顺序。

 

·         到位；即，只需要一定量的O（1）的额外的存储空间

 

·         •在线;即，可以对列表排序，因为它接收它

 

 

 

 

 

四：JAVA如何实现归并排序

 

public class InsertionSort {
	
	public static void insertionSort(Comparable []data){//升序排序方法
	        for(int index=1;index0 && data[position-1].compareTo(key)>0){  
	                data[position] = data[position-1];  
	                position--;  
	            }  
	            data[position]=key;  
	        }
	 }  
	 
	 public static void insertionSort(int[] num){ //降序排序方法
	      int j;                  //到目前已排序的元素数
	      int key;                //要被插入的元素 Key
	      int i;  
	      for (j = 1; j < num.length; j++)    //从1开始不是0
	      {
	           key = num[ j ];
	           for(i = j - 1; (i >= 0) && (num[ i ] < key); i--)   // 元素小的正在移动...
	           {
	                  num[ i+1 ] = num[ i ];
	           }
	          num[ i+1 ] = key;    //把元素key放在适当的位置
	      }
	 }
	 
    public static void main(String []args){  
        Comparable[] c ={4,9,23,1,45,27,5,2};  
        insertionSort(c);  
        for(int i=0;i

 

 

 

 

 

五：算法复杂度

 
空间复杂度O(1)
时间复杂度O(n²)
最差情况：反序，需要移动n*(n-1)/2个元素
最好情况：正序，不需要移动元素

 

 

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需(n-1)次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为O(n²)。

 

因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。 插入排序在工业级库中也有着广泛的应用，在STL的sort算法和stdlib的qsort算法中，都将插入排序作为快速排序的补充，用于少量元素的排序（通常为8个或以下）。

 

 

 

参考资料：

 http://zh.wikipedia.org/wiki/%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F

 http://blog.csdn.net/cjf_iceking/article/details/7916194

 http://www.cnblogs.com/fanyong/archive/2012/03/23/2413553.html

 http://www.cnblogs.com/Clingingboy/archive/2011/09/12/2174140.html

 https://www.princeton.edu/~achaney/tmve/wiki100k/docs/Insertion_sort.html

http://mathbits.com/MathBits/Java/arrays/InsertionSort.htm