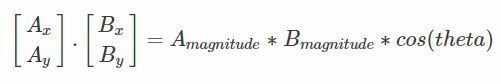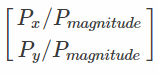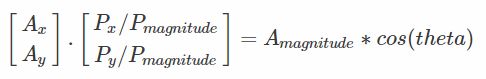踫撞检测 之三 — 使用分离轴理论进行踫撞检测（Collision Detection Using the Separating Axis Theorem）（完整翻译）

因为有踫撞的活要干，所以找了点资料，顺便译完之前一篇“入门文章”，再译一下这个详细一点的 — 使用分离轴理论进行踫撞检测（Collision Detection Using the Separating Axis Theorem）（完整翻译）

有些意译的会放上原文参考，有错的地方留言指正，及时更改， 感谢
如果想转请评论留个言并注明原博 @Sclifftop https://blog.csdn.net/S_clifftop/article/details/108454743

点赞，不然砍你

---

分离轴理论（以下简称SAT）经常被用于检测两个简单的多边形或者一个多边形和一个圆形，当然，他也会有利弊，接下来，我们会深究此理论所用到的数学知识，然后用一些代码示例和小demo去演示如何应用于游戏中

注意：尽管demo和一些代码示例用的是flash和AS3语言，但原理都是一样的，语言并不重要，看原理就完事

---

这个理论讲了什么？

说白了，SAT讲的是：如果你能用一条线把两个多边形分开，那这两个多边形就没有接触（他的总结与第一篇不一样，但问题不大）

将上图分为两行，第二行的多边形都有接触，因为你很难在两个物体之间画一条不与任何物体接触的线，但是第一行就很容易了，别说一条，你画一万条都没人管你，如下：

好了，小爷不跟你开玩笑了（鸡叫），还是上面那个总结：如果你可以轻松地在两个物体之间画一条线，那两者之间一定有间隙

---

沿任意一个轴线投影

假设两个多边形为正方形（box1，box2），图中的两个正方形是没有接触，那该怎么去算呢（你看起来没有接触就是不接触？你还看你自己觉得，记住，看到的不一定是对的）

从代码角度来分析：计算两个正方形之间的水平距离，然后减去box1和box2各自宽度的一半，与0比较就能得出是否接触

//伪代码，其实也不伪了
var length:Number = box2.x - box1.x;
var half_width_box1:Number = box1.width*0.5;
var half_width_box2:Number = box2.width*0.5;
 
var gap_between_boxes:Number = length - half_width_box1 - half_width_box2;
if(gap_between_boxes > 0) trace("It's a big gap between boxes")
else if(gap_between_boxes == 0) trace("Boxes are touching each other")
else if(gap_between_boxes < 0) trace("Boxes are penetrating each other")

如果两个正方形是其他方向呢？我们将它们旋转一下：

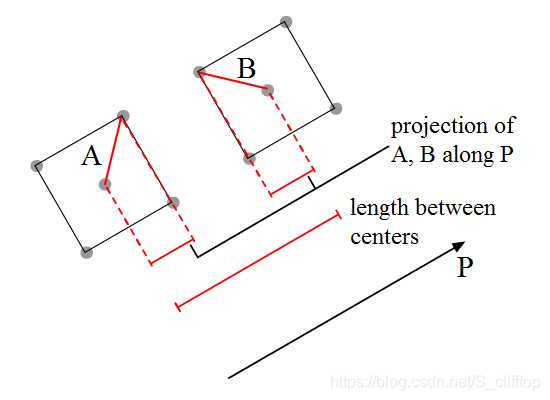
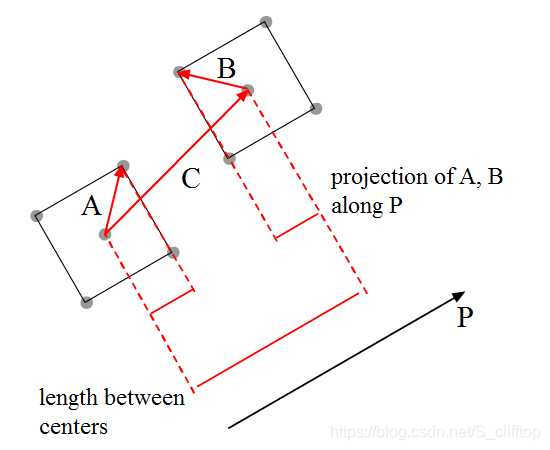
尽管我们知道间隙的值是不变，但是这种情况下该怎么计算呢 （上图投影的轴线是与P的方向平形）

这个时候向量就有用处了，我们需要把向量A和向量B投影到轴线P上，这样就能得到宽度的一半

---

有些同学可能对某些数学知识有所遗忘，那我们就先来稍微复习一下：

向量

先让我们看下向量A、B之间的数量积：

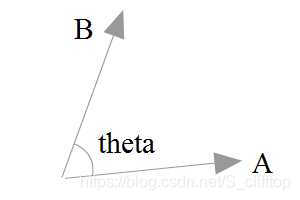
我们可以用两个向量来进行定义数量积（点积公式）：

​
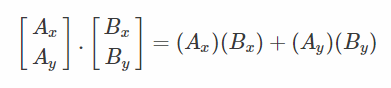
也可以用向量的大小和两者之间的角度来表示数量积（magnitude指的是一个量的大小，与方向无关，是个标量，后面我说某个向量的标量，你知道是magnitude就行了，例如：向量A的标量）：

接下来，算下向量A在向量P上的投影：

上图所示，我们知道如何计算A投影在P方向上的长度：A（注：A的标量）*cos(theta)（theta是向量A与向量P之间的夹角）

尽管我们可以直接根据角度来计算出投影的大小，但是会有点繁琐，得需要找一个直接的方法：

注意：表示单位向量（模等于1）

根据图中的推导，我们现在就可以用左边的公式

---

接下来讲讲该如何应用

为了方便，图中已标注了每个点的名称：

根据公式就可以按下图去算投影值：

计算间隙，需要计算几个的长度：

• 向量A在轴线P上的投影
• 向量B在轴线P上的投影
• 向量C在轴线P上的投影

需要特别注意箭头的方向，向量A与C是正向，它们投在轴线P上的是正值，向量B是反向，那么投影出来的则是负值

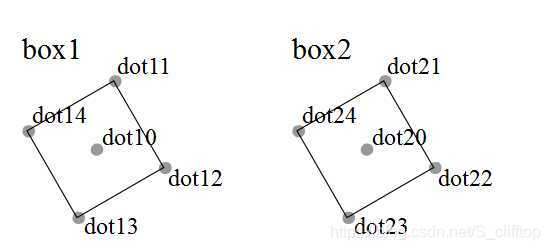
根据以上分析，代码思路就很清晰了，如下：

var dot10:Point = box1.getDot(0);
var dot11:Point = box1.getDot(1);
 
var dot20:Point = box2.getDot(0);
var dot24:Point = box2.getDot(4);
 
//Actual calculations
var axis:Vector2d = new Vector2d(1, -1).unitVector;
var C:Vector2d = new Vector2d(
    dot20.x - dot10.x,
    dot20.y - dot10.y
)
var A:Vector2d = new Vector2d(
    dot11.x - dot10.x,
    dot11.y - dot10.y
)
var B:Vector2d = new Vector2d(
    dot24.x - dot20.x,
    dot24.y - dot20.y
)
var projC:Number = C.dotProduct(axis)
var projA:Number = A.dotProduct(axis);
var projB:Number = B.dotProduct(axis);
 
var gap:Number = projC - projA + projB; //projB is expected to be a negative value
if (gap > 0) t.text = "There's a gap between both boxes"
else if (gap > 0) t.text = "Boxes are touching each other"
else t.text = "Penetration had happened."

（此处有个可交互的小demo，但是我访问时没有显示出来，可以去看下：原文）

其余代码请点击：点俺就送屠龙刀，一刀999999，爽到大小便失禁，爽到连自己都打

---

不足之处

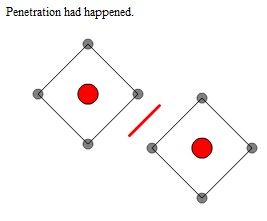
一：向量A和B得是固定的，如果你交换下两个正方形的位置，之前所说的踫撞检测就没用了

（交换两个正方形位置就会穿透）（两个物体之间的间隙）

二：两个正方形在一个方向有重叠，下图就没办法算出来了（瞅你这一天天的，看见就来气）

上面的代码是有不足，主要为了让我们知道原理，接下来优化一下

第一种不足的解决方法

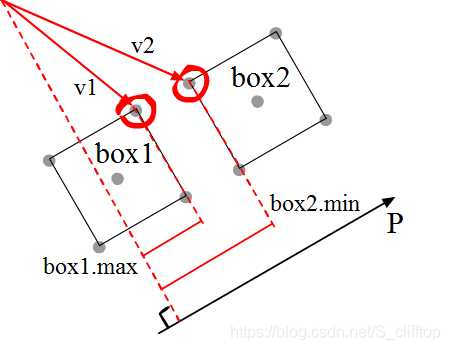
首先，我们需要找出在轴线P上角最大和最小的投影（下图就是相对左上角那个汇聚的点）

上图中两个物体的朝向是很理想的情况（刚好都与轴线P平行），这样比较好找，但是如果box1和box2与轴线P有夹角呢？

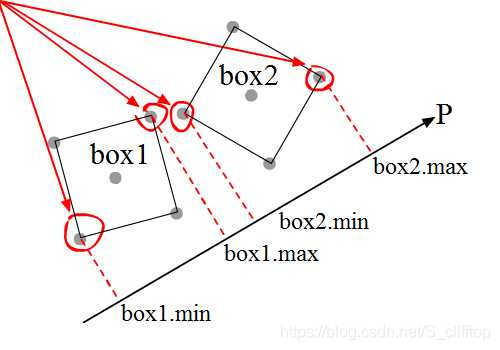
上图中两个正方形就不是很乖，但是既然已经这样了，也不能手动给它摆成平行，这就得遍历每个角去寻找最大和最小值

经过寻找得到了最小和最大的投影值，接下来就要计算是否有踫撞了，那么问题来了，怎么算咧？

上图标了box1.max和box2.min在轴线P上的投影

图中两个正方形（box1，box2）之间有间隙，因为box2.min - box1.max > 0，也就是box2.min > box1.max，交换一下两个正方形的位置，box1.min > box2.max也能得出两个正方形间没有接触，用代码表示：

//SAT: 判断box1和box2之间的间隙Pseudocode to evaluate the separation of box1 and box2
if(box2.min>box1.max || box1.min>box2.max){
    trace("collision along axis P happened")
}
else{
    trace("no collision along axis P")
}

---

更详细的代码

注意下面这些代码是没有优化过的，主要目的是让你们知道原理

1. 向量初始：

//preparing the vectors from origin to points
//since origin is (0,0), we can conveniently take the coordinates 
//to form vectors
var axis:Vector2d = new Vector2d(1, -1).unitVector;
var vecs_box1:Vector. = new Vector.;
var vecs_box2:Vector. = new Vector.;
 
for (var i:int = 0; i < 5; i++) {
    var corner_box1:Point = box1.getDot(i)
    var corner_box2:Point = box2.getDot(i)
     
    vecs_box1.push(new Vector2d(corner_box1.x, corner_box1.y));
    vecs_box2.push(new Vector2d(corner_box2.x, corner_box2.y));
}

2. 接下来获取box1上面最小最大的投影值，对box2的操作是一样的就不再写了

//setting min max for box1
var min_proj_box1:Number = vecs_box1[1].dotProduct(axis); 
var min_dot_box1:int = 1;
var max_proj_box1:Number = vecs_box1[1].dotProduct(axis); 
var max_dot_box1:int = 1;
 
for (var j:int = 2; j < vecs_box1.length; j++) 
{
    var curr_proj1:Number = vecs_box1[j].dotProduct(axis)
    //select the maximum projection on axis to corresponding box corners
    if (min_proj_box1 > curr_proj1) {
        min_proj_box1 = curr_proj1
        min_dot_box1 = j
    }
    //select the minimum projection on axis to corresponding box corners
    if (curr_proj1> max_proj_box1) {
        max_proj_box1 = curr_proj1
        max_dot_box1 = j
    }
}

3. 最后判断间隔的值

var isSeparated:Boolean = max_proj_box2 < min_proj_box1 || max_proj_box1 < min_proj_box2
if (isSeparated) t.text = "There's a gap between both boxes"
else t.text = "No gap calculated."

（此处，可交互的小demo，我访问时没有显示出来，去看下：原文）

其余代码请点击：点俺，看后喷水

优化

如果你不想这么复杂，其实还可以优化 — 不计算P的单位向量，因为这种计算会涉及到勾股定理那就要用到的Math.sqrt()（开平方根）会影响效率（说到这不得不提一下卡神，那个拥有D的意志的男人，现在都是封装的接口，还有几个人会研究底层的，帅得不谈）

推理公式如下（一些变量名称看上图）：

/*
Let:
//用P_unit表示P的单位向量
P_unit be the unit vector for P,
//用P_mag表示P的标量
P_mag be P's magnitude,
//用v1_mag表示v1的标量
v1_mag be v1's magnitude,
//v2_mag表示v2的标量
v2_mag be v2's magnitude,
//theta_1是v1与P之间的夹角
theta_1 be the angle between v1 and P,
//theta_2是v2与P之间的夹角
theta_2 be the angle between v2 and P,
 
Then:
box1.max < box2.min
=> v1.dotProduct(P_unit) < v2.dotProduct(P_unit)
=> v1_mag*cos(theta_1) < v2_mag*cos(theta_2)
*/

我们都知道，不等式两边同乘相同的数是不影响符号的：

/*
So:
A*v1_mag*cos(theta_1) < A*v2_mag*cos(theta_2)
 
If A is P_mag, then:
P_mag*v1_mag*cos(theta_1) < P_mag*v2_mag*cos(theta_2)
...which is equivalent to saying:
v1.dotProduct(P) < v2.dotProduct(P)
*/

经过推论可以得出不需要单位向量也能检测是否重叠

如果你只是检测是否重叠，就使用这种方法就可以了，但是要计算box1和box2重叠的部分（大部分游戏都需要计算的），你还是得计算P的单位向量

第二种不足解决方法

之前说了，如果有部分重叠，只投一个方向是不行的，得结合其他方向一起判断，但是你知道要哪个方向吗？（你可能会说知道，行，还好是法治社会，不然你早就被动当0了）

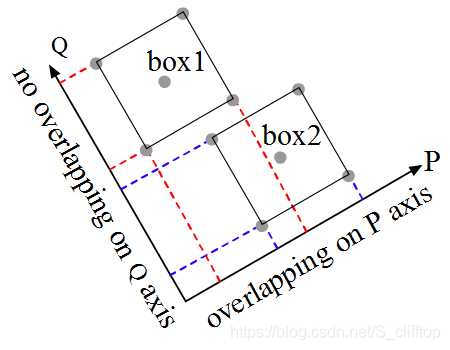
看上图，如果是这种情况，就很好办，用个暴力的方法，直接判断轴线Q和轴线P，如果至少一个没有重叠，那两个正方形就是没有踫撞

但如果有角度不是平行的呢？

（此处，小demo，没有显示出来，去看下：原文）

该怎么判断？下面我们就取多边形的法线来判断

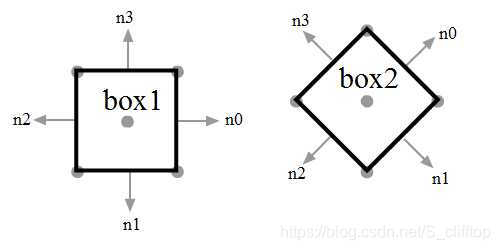
一般来说，都会去检测8条：两个正方形的n0 - n3，同志们，让我们来看一下：

• n0 and n2 of box1
• n1 and n3 of box1
• n0 and n2 of box2
• n1 and n3 of box2

分析完就知道，我们不必去搞8条，4条就完事，极限一点，相同方向的就需要检测2条

但是其他多边形呢？

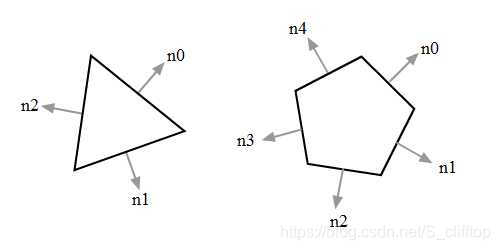
很幸运，捷径只有一条，我不是在说笑，所以我们得遍历所有的轴线去判断

法线的计算

每个面都会有两条法线：

上图标出了P的两条法线，注意向量不一样的部分和它们的符号

一般习惯上都是顺时针方向，所以我用了左侧的法线来判断，看下我写的方法（在文件SimpleSquare.as中）

public function getNorm():Vector. {
    var normals:Vector. = new Vector.
    for (var i:int = 1; i < dots.length-1; i++) 
    {
        var currentNormal:Vector2d = new Vector2d(
            dots[i + 1].x - dots[i].x, 
            dots[i + 1].y - dots[i].y
        ).normL //left normals
        normals.push(currentNormal);
    }
    normals.push(
        new Vector2d(
            dots[1].x - dots[dots.length-1].x, 
            dots[1].y - dots[dots.length-1].y
        ).normL
    )
    return normals;
}

看下怎么判断

下面列好所有的情况，应该能看懂，自己也可以优化一下：
···
//results of P, Q
var result_P1:Object = getMinMax(vecs_box1, normals_box1[1]);
var result_P2:Object = getMinMax(vecs_box2, normals_box1[1]);
var result_Q1:Object = getMinMax(vecs_box1, normals_box1[0]);
var result_Q2:Object = getMinMax(vecs_box2, normals_box1[0]);

//results of R, S
var result_R1:Object = getMinMax(vecs_box1, normals_box2[1]);
var result_R2:Object = getMinMax(vecs_box2, normals_box2[1]);
var result_S1:Object = getMinMax(vecs_box1, normals_box2[0]);
var result_S2:Object = getMinMax(vecs_box2, normals_box2[0]);

var separate_P:Boolean = result_P1.max_proj < result_P2.min_proj ||
result_P2.max_proj < result_P1.min_proj
var separate_Q:Boolean = result_Q1.max_proj < result_Q2.min_proj ||
result_Q2.max_proj < result_Q1.min_proj
var separate_R:Boolean = result_R1.max_proj < result_R2.min_proj ||
result_R2.max_proj < result_R1.min_proj
var separate_S:Boolean = result_S1.max_proj < result_S2.min_proj ||
result_S2.max_proj < result_S1.min_proj

//var isSeparated:Boolean = separate_p || separate_Q || separate_R || separate_S
if (isSeparated) t.text = “Separated boxes”
else t.text = “Collided boxes.”
···
作者在这里写了一堆，主要就一个意思：上面 separate_P、separate_Q、separate_R、separate_S中只要有一个是true，后面的就不用再算了，可以省了很多不必要的运算，由你来优化

（此，demo，没显，去看：原文）

后感

经过上面的规则计算，可以检测轴线是否有重叠，我需要提两点：

• 在任何边都没有重叠的情况下，SAT 检测其中一边有重叠就不会再继续下去了，但是如果有重叠，它会遍历所有边，直到找出来，根据separate_p || separate_Q || separate_R || separate_S，即使只有 separate_S是重叠的，那它也会把前面的判断完，这种情况下效率就比较低
• SAT是遍历多边形的边来进行判断，所以多边形越复杂，程序就越复杂

六边形 - 三角形踫撞检测

下面一小段代码是一个六边形和三角形之间的检测：

private function refresh():void {
//prepare the normals
var normals_hex:Vector. = hex.getNorm();
var normals_tri:Vector. = tri.getNorm();
 
var vecs_hex:Vector. = prepareVector(hex);
var vecs_tri:Vector. = prepareVector(tri);
var isSeparated:Boolean = false;
 
//use hexagon's normals to evaluate
for (var i:int = 0; i < normals_hex.length; i++) 
{
    var result_box1:Object = getMinMax(vecs_hex, normals_hex[i]);
    var result_box2:Object = getMinMax(vecs_tri, normals_hex[i]);
     
    isSeparated = result_box1.max_proj < result_box2.min_proj || result_box2.max_proj < result_box1.min_proj
    if (isSeparated) break;
}
//use triangle's normals to evaluate
if (!isSeparated) {
    for (var j:int = 1; j < normals_tri.length; j++) 
    {
        var result_P1:Object = getMinMax(vecs_hex, normals_tri[j]);
        var result_P2:Object = getMinMax(vecs_tri, normals_tri[j]);
         
        isSeparated = result_P1.max_proj < result_P2.min_proj || result_P2.max_proj < result_P1.min_proj
        if (isSeparated) break;
    }
}
 
if (isSeparated) t.text = "Separated boxes"
else t.text = "Collided boxes."
}

完整代码在DemoSAT4.as中：点俺点点点点点点点俺

（demo，没，看：原文）

正方形 - 圆形踫撞检测

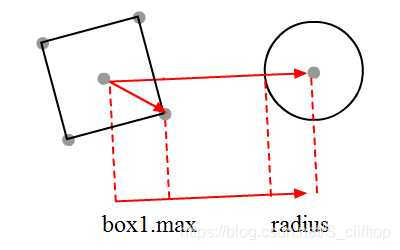
检测圆形之间的踫撞相对比较简单，因为每个方向一样（就绕着圆转呗，害能咋滴）：

private function refresh():void {
    //prepare the vectors
    var v:Vector2d;
    var current_box_corner:Point;
    var center_box:Point = box1.getDot(0);
     
    var max:Number = Number.NEGATIVE_INFINITY;
    var box2circle:Vector2d = new Vector2d(c.x - center_box.x, c.y - center_box.y)
    var box2circle_normalised:Vector2d = box2circle.unitVector
     
    //get the maximum
    for (var i:int = 1; i < 5; i++) 
    {
        current_box_corner = box1.getDot(i)
        v = new Vector2d(
            current_box_corner.x - center_box.x , 
            current_box_corner.y - center_box.y);
        var current_proj:Number = v.dotProduct(box2circle_normalised)
         
        if (max < current_proj) max = current_proj;
    }
    if (box2circle.magnitude - max - c.radius > 0 && box2circle.magnitude > 0) t.text = "No Collision"
    else t.text = "Collision"
}

来了来了，本文总结

balabalabalabala……，感谢祖国培养，感谢父母养育 ，完。

---

粗略看一遍你什么都记不住，只有会记得开头：SAT讲的是：如果你能用一条线把两个多边形分开，那这两个多边形就没有接触，所以结合代码来看好吧

---