剑指offer 40. 最小的k个数

题目链接
输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]
示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

方法1：大根堆

构建堆+堆排序可参考视频

大根堆的性质：

1.完全二叉树
2.父节点>子节点

堆排序：
1.对于一个大根堆，每次将堆顶和堆中最后一个元素交换，堆的大小-1
2.对堆顶调用heapfiy使其保持堆结构
3.重复该过程知道堆有序

堆排序转载自链接
比较直观的想法是使用堆数据结构来辅助得到最小的 k 个数。堆的性质是每次可以找出最大或最小的元素。我们可以使用一个大小为 k 的最大堆（大顶堆），将数组中的元素依次入堆，当堆的大小超过 k 时，便将多出的元素从堆顶弹出。我们以数组
[5,4,1,3,6,2,9]，k=3 为例展示元素入堆的过程，如下面动图所示：

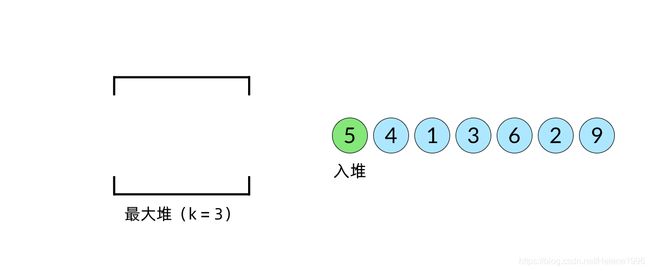
这样，由于每次从堆顶弹出的数都是堆中最大的，最小的 k 个元素一定会留在堆里。这样，把数组中的元素全部入堆之后，堆中剩下的 k 个元素就是最大的 k 个数了。

注意在动画中，我们并没有画出堆的内部结构，因为这部分内容并不重要。我们只需要知道堆每次会弹出最大的元素即可。在写代码的时候，我们使用的也是库函数中的优先队列数据结构，如 Java 中的 PriorityQueue。在面试中，我们不需要实现堆的内部结构，把数据结构使用好，会分析其复杂度即可。

代码实现

//保持堆的大小为k,然后遍历数组中的数字，遍历的时候作如下判断：
//1.若目前堆的大小小于k，将当前数字放入k中
//2.否则判断当前元素与大根堆堆顶元素的大小关系，若小于堆顶元素，先poll掉堆顶，再将该数字放入堆中
//3.若当前元素比大根堆堆顶小，先poll掉堆顶，再将该数字放入堆中

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if(k == 0 || arr.length == 0){
            return new int[0];
        }
        //默认是小根堆，实现大根堆需要重写一下比较器
        Queue pq = new PriorityQueue<>((v1,v2) -> v2-v1);
        for(int num:arr){
            if(pq.size() < k){
                pq.offer(num);
            }else if(num

方法2：快速排序

将原数组快速排序，然后选取数组的前k个数
快排思想可参考链接

快排思想：

1. 先从数列中取出一个数作为基准数。
2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3. 再对左右区间重复这一步骤，直到各区间只有一个数。

具体实现：

• 将nums[low]的值赋给基准数pivot ,(pivot=nums[low])
• 指针j从右向左遍历数组直到j指向第一个比pivot小的数，指针i从左向右遍历数组直到找到第一个比pivot大的数
• 交换nums[I]和nums[j]的值
• 重复这一操作直至i>=j
• 将pivot的值赋给nums[j],将nums[j]的值赋给nums[low]，此时nums[j]左边的数均小于nums[j],nums[j]右边的数均大于nums[j]
• 对nums[j]左侧和右侧的区间重复以上步骤直至各区间只有一个数,( if(low>=high) return;)

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if(k == 0 || arr.length == 0){
            return new int[0];
        }
        else{
            quickSort(arr,0,arr.length-1);
            return Arrays.copyOf(arr, k);
        }
    }

    private void quickSort(int[] nums, int low, int high){
        //当数组长度为小于等于1时返回
        if(low>=high) return;
        int pivot =nums[low];
        int i = low, j = high;
        int t = 0;
        while(true){
            //从右往左找寻第一个比基准v小的数
            while(j>low&&nums[j]>=pivot){
                j--;
            }
            //从左往右找第一个比基准v大的数
            while(i=j){
                break;
            }
            //交换i和j的值
            t = nums[j];
            nums[j]=nums[i];
            nums[i]=t;
        }
        //将pivot的值和nums[j]的值交换
        nums[low]=nums[j];
        nums[j]=pivot;
        //对j的左右两侧进行快排
        quickSort(nums,j+1,high);
        quickSort(nums,low,j-1);
    }
}