LeteCode刷题：416. 分割等和子集（中等难度)

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100
数组的大小不会超过 200

示例 1:

输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/partition-equal-subset-sum

解析：首先由题意正整数和非空，能分成两个等集合，则数组和sums必须是偶数，sums%2==0能被2整除，其次里面的数进行组合相加要能等于target=sum/2,否则无法分成两部分。这道题就变成了，集合nums中是否存在几个数相加等于target。

  题目给的数组大小不会超过200，元素不会超过100，暴力搜索的话，100*100=10000复杂度也不会太高，计算机基本能完成。所以可以尝试计算出所有组合的和，看是否等于sums/2。
当然这道题还可以用动态规划来做,作为算法题，应该优先考虑动态规划的解法：

一、动态规划思路：

 建立二维表格dp，dp[i][j]表示nums[0]~nums[i]之间的数，是否能经过一系列组合得到j，能的话dp[i][j]=True，反之False。我们的目标就是要知道dp[len(nums)-1][target]是True还是False

判断转移条件：当前nums[i] whether == j:

nums[i]>j	dp[i][j]=dp[i-1][j]	不选用，查找下一个数
nums[i]<=j	dp[i][j]=dp[i-1][j-nums[i]]	选用当前数

边界条件：
由上表可知，我们首先要初始化i=0的情况，然后遍历i从1开始，这样才能保证i-1！=负数，
dp[0][j]表示，nums[0]是否等于j，所以只有dp[0][nums[0]]=True其他情况都是False。当然前提是nums[0]<=target否则就超出表的边界了。
代码:

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        leng=len(nums) # 数组总数
        target,remain=sums=divmod(sum(nums),2) # 得到target并判断是否是偶数
        if remain :
            return False # 如果不是偶数，肯定不能分成两部分整数
        dp=[[False for _ in range(target+1)  ] for _ in range(leng)]
        # 先分析下：如果nums[i]==j,则 dp[i][j]=True
        #如果nums[i]>j,dp[i][j]=dp[i-1][j]         # 从这里可以看出我们需要对i=0这一列初始化，
        											#否则i-1可能是负数，计算从i=1开始
        #如果 nums[i]
        # 初始化 
        # for j in range(target+1):
        #     if nums[0]==target:
        if nums[0]<=target:  # 判断第一个数是否超出边界，如果超出了 那肯定也不能分成两部分
            dp[0][nums[0]]=True# 只有这个是true 其他一定都是false
        else: 
            return False
    
        # i 表示长度区间，从1开始，上面已经说了i=0这一行已经初始化过了
        for i in range(1,leng):
            #j表示当前的目标值
            for j in range(target+1):
                # if nums[i] == j:
                #     dp[i][j]=True
                dp[i][j]= dp[i-1][j] or dp[i-1][j-nums[i]] #两种情况只要有一个是true结果就是true
                #原本应该这样写：
                 #if j >= nums[i]:
                 #   dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]]
                #else:
                #    dp[i][j] = dp[i - 1][j]
				# 但是通过列出表格可以看到即使j-nums[i]是负数，得到的结果依然没有影响，主要是or的作用
				#只要同一列的都是True，其实这也算特殊性吧，实际设计的思路是要考虑这种情况的
        return dp[-1][-1]   # dp[leng-1][target]

执行用时 :1624 ms, 在所有 python3提交中击败了31.99%的用户
内存消耗 :17.7 MB, 在所有 python3提交中击败了5.82%的用户

降二维数组为一维数组，由于每次当前位置都有上一行以及左上值决定，下一行是把上一行先完全复制即dp[i-1][j]，在根据上一行的转移状态dp[i-1][j-nums[i]]来共同决定的。所以这个复制上一行状态完全可以省略，只需要每次根据之前状态和转移状态决定就可以了。变成一维数组,数组的状态，从原来二维数组的第一行一直更新到最后一行，就是我们要的最终状态。

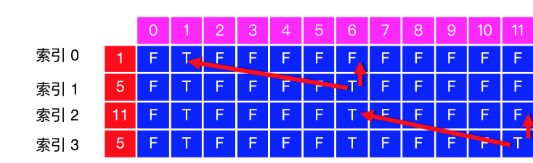
借用letecode别人画的图，第一行如果确定下来了，从第二行开始，先依据第一行的状态，在查看转移状态，比如第二行，先copy第一行状态，然后[1,6]位转移状态是对应的[0,1]为True，所以跟新为True

重新定义dp表的意义，dp[j]表示j是否能被nums里面的数表示。
转移判定为是否使用nums[i]。 是：dp[j]=dp[j-nums[i]] 否：dp[j]=dp[j] 沿用之前状态
代码：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        leng=len(nums)
        target,remain=sums=divmod(sum(nums),2)
        if remain :
            return False
        dp=[False for _ in range(target+1)  ]
        # 先分析下:
        #初始状态：就是二维数组的第一行初始状态
        #dp[nums[0]]的位置是True，其他都是False
        #开始跟新：
        #同二维数组，只不过i-1的操作可以省略，直接是当且一维表
        #注意：这里列的遍历需要逆序，因为在二维表中，我们是从上一行左侧开始寻找值，也就是说一维在跟新的时候，必须维持原来的状态（对应二维数组的上一行）的左侧。
        #所以跟新状态应该从右到左跟新，才能保证右侧的状态先跟新，寻找左侧的时候还是原来的状态
         
        if nums[0]<=target:
            dp[nums[0]]=True# 只有这个是true 其他一定都是false
        else: 
            return False
        # i 表示长度区间
        for i in range(1,leng):
            #j表示当前的目标值
            dp[-1]=dp[-1] or dp[target-nums[i]]
            if dp[-1]==True :
                return True
            for j in range(target-1,0,-1):  # 0不需要计算
                # if nums[i] == j:
                #     dp[j]=True
                #     continue
                if j>= nums[i]:
                    dp[j]=dp[j] or dp[j-nums[i]]
                # else:
                #     break  #如果j
 
        return dp[target]
        

执行用时 :580 ms, 在所有 python3 提交中击败了78.06%的用户
内存消耗 :12.8 MB, 在所有 python3 提交中击败了99.03%的用户

“哈希迭代”：
找出所有可能的组合，并判断target是否在组合里面
代码设计:比如一个集合里面有{t1,t2,t3}那么他们的组合列表是{t1,t2,t3,t1+t2,t1+t3,t2+t3},如果组合到了target就可以提前结束搜寻。

但是这样所有组合保存，可能造成内存溢出，我们只关注组合的数值，而不需要关注具体组合的数，所以可以把不同组合但是最后数值相同的组合，只保留一个数值就可以了。比如t1+t2==t1+t3==t3+t4=6那么只要保存一个6就可以了。注意这里的组合方式还是比较有意思的。每次组合是在之前的基础上的累加，有点类似于树搜索。

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        leng=len(nums)
        target,remain=sums=divmod(sum(nums),2)
        if remain :
            return False
        ans={
     0} # 收集组合的集合，set的话可以去重，因为只关注组合的数值，而不需要关注具体组合的数,防止内存溢出
        for i in nums:
            for j in list(ans): # 这个集合会在迭代过程中改变，所以需要转换为List
                j+=i
                if j==target:
                    return True
                ans.add(j)
        return False

执行用时 :292 ms, 在所有 python3 提交中击败了87.26%的用户
内存消耗 :12.8 MB, 在所有 python3 提交中击败了99.03%的用户
这种方法速度反而更快，对比动态规划的方法，其实也是设置了数值保存可能的组合值，但是这里有去重的操作，所以总的遍历要少。

使用Bitset数据结构记录：
这种方法的思路其实和上面是一样的，保存所有组合的可能值，但是用的是二进制的数据结构储存，在内存和速度上都有极大的优势！

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        flag = 1                        # 初始化
        sumnums = 0
        for i in nums:
            sumnums += i                # 记录和
            flag = flag | flag << i     # 记录所有可能的结果

        if sumnums % 2 == 0:            # 和为偶数才有解
            sumnums //= 2
        else:
            return False
        target = 1 << sumnums           # 目标和

        if target & flag != 0:          # 目标位置上不为0
            return True
        else:
            return False

执行用时 :64 ms, 在所有 python3 提交中击败了93.22%的用户
内存消耗 :12.8 MB, 在所有 python3 提交中击败了100.00%的用户