NN学习中的技巧之(一) 参数的最优化之SGD
源码在前,了无秘密
NN的学习实质上就是区找到使得损失函数最小的那组参数,包括权重和偏置,所以这就是一个参数寻优的过程,是最优化问题。但NN中的参数空间非常庞大,网络越深参数空间越大,这使得NN的参数寻优不可能通过解析的方法实现。
SGD(Stochastic Gradient Descent)随机梯度下降
在NN的学习中,找最优参数通常是以梯度为线索的,使用最终的损失函数计算值关于每个参数的梯度,沿着梯度的反方向更新参数,重复多次逐渐靠近最优参数,每次以整个训练数据集的一个小batch的数据求一次损失函数值(batch中所有输入的损失函数的和),并计算此损失函数值关于所有参数的梯度,以梯度计算值为依据根据梯度下降法更新一次参数,直到迭代次数达到为止。
随机体现在每个iteration随机从训练数据中选出一个batch。
SGD表现不好的例子:
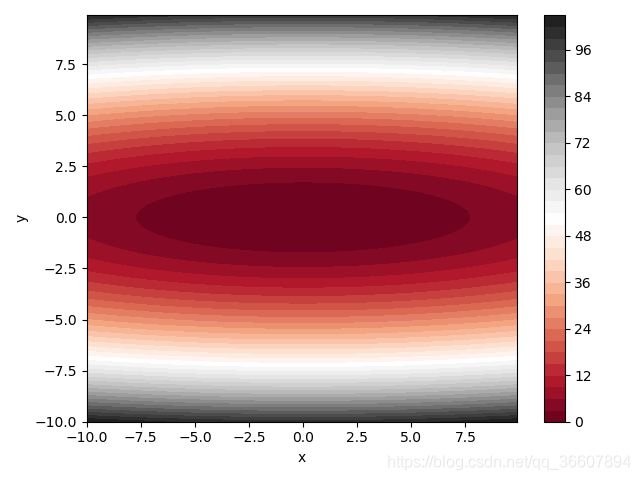
二元函数 f ( x , y ) = 1 20 x 2 + y 2 f(x,y)=\frac{1}{20}x^2+y^2 f(x,y)=201x2+y2
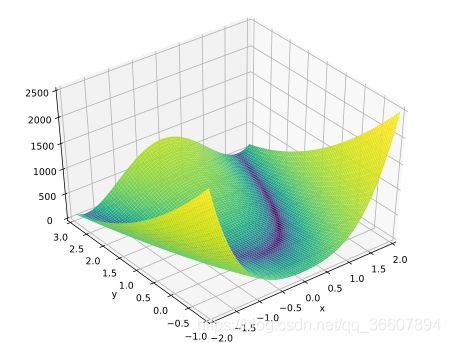
函数图像:
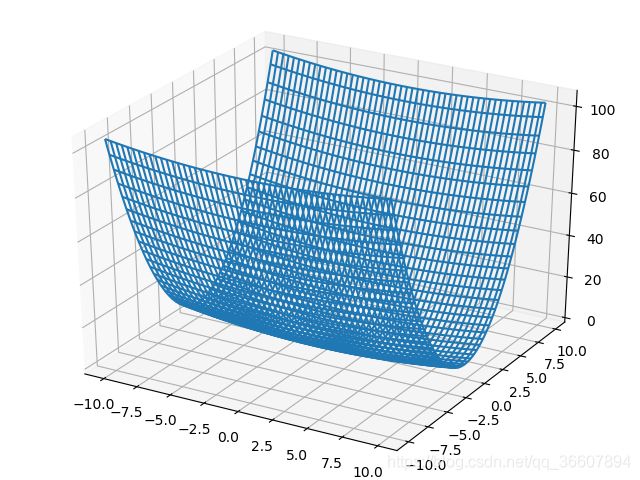
函数的等高线:
画图代码:
# SGD_Nogood_Example.py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x, y):
return (x ** 2) / 20 + y ** 2
# 画函数图像
fig = plt.figure()
ax = Axes3D(fig)
x = np.arange(-10, 10, 0.1)
y = np.arange(-10, 10, 0.1)
X, Y = np.meshgrid(x, y)
Z = func(X, Y)
ax.plot_wireframe(X, Y, Z)
# 画函数的等高线
plt.figure()
# 进行颜色填充,其他着色方案:
# cmap=plt.cm.Blues plt.cm.hot
# plt.cm.Accent plt.cm.cbook cmap='jet'
plt.contourf(X, Y, Z, 40, cmap='RdGy')
plt.colorbar()
# 画等高线(可画可不画),前面只填充了颜色,也足够表现出等高线
# contour = plt.contour(X, Y, Z, 40, colors='black')
# 画40条等高线
plt.xlabel('x')
plt.ylabel('y')
# plt.savefig('0.png', dpi=100)
# 线条标注的绘制
# plt.clabel(contour, inline=True, fontsize=10)
# 去掉坐标轴刻度
# plt.xticks(())
# plt.yticks(())
# plt.axis('off')与上两句同效,但无法显示xlabel和ylabel
plt.show()
梯度图:
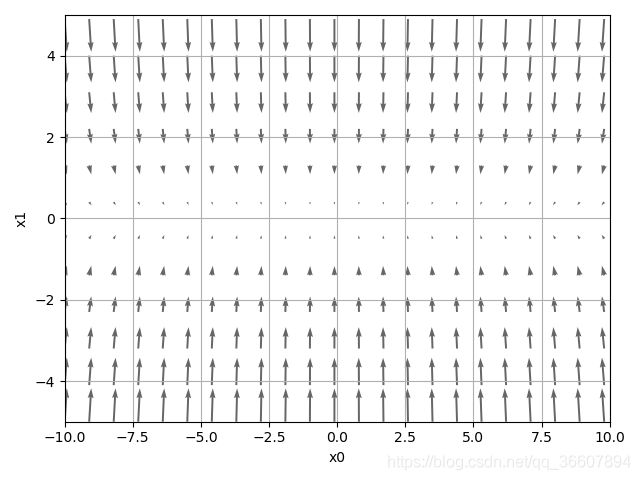
可以看出沿着x方向的梯度基本都接近于0,这就导致SGD不好学习了。
梯度图绘制代码:
# Quiver.py
# 使用quiver函数绘制f(x,y)=0.05x^2+y^2的梯度图
import numpy as np
import matplotlib.pyplot as plt
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
fxh1 = fxh1[idx[1]] # 完美改造!!!
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
fxh2 = fxh2[idx[1]] # 完美改造!!!
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
def func(x):
out = x[0]**2 / 20 + x[1]**2
return out
if __name__ == '__main__':
x0 = np.arange(-10.0, 10.0, 0.9)
x1 = np.arange(-5.0, 5.0, 0.9)
X, Y = np.meshgrid(x0, x1)
X = X.flatten()
Y = Y.flatten()
grad = numerical_gradient(func, np.array([X, Y]))
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy", color="#666666")
# quiver进行箭图绘制,X,Y是箭头位置,U,V是箭头数据,angles="xy"用于绘制梯度场
# ,headwidth=10,scale=40,color="#444444")
plt.xlim([-10, 10])
plt.ylim([-5, 5])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.draw()
plt.show()
之前我的这篇博客绘制过 f ( x , y ) = x 2 + y 2 f(x,y)=x^2+y^2 f(x,y)=x2+y2的图像和梯度图等,这次绘制 f ( x , y ) = 1 20 x 2 + y 2 f(x, y)=\frac{1}{20}x^2+y^2 f(x,y)=201x2+y2,直接对之前的代码做了少许改进实现的,主要是改了梯度计算方法,不再使用非批版本输入的数值梯度方法,而是使用numpy的nditer对象实现二维矩阵索引实现数值梯度,花了俩小时才搞定,不容易的。。。
需要再次记录一下,使用python时,输入数字时如果是浮点型一定要加小数点,例如输入10和10.0,python会自动判断为整型和浮点型,在程序中10+0.0001=10,而10.0+0.0001=10.0001,前面的结果会导致梯度计算完全错误!!!
已经是第二次掉到这个坑里了。
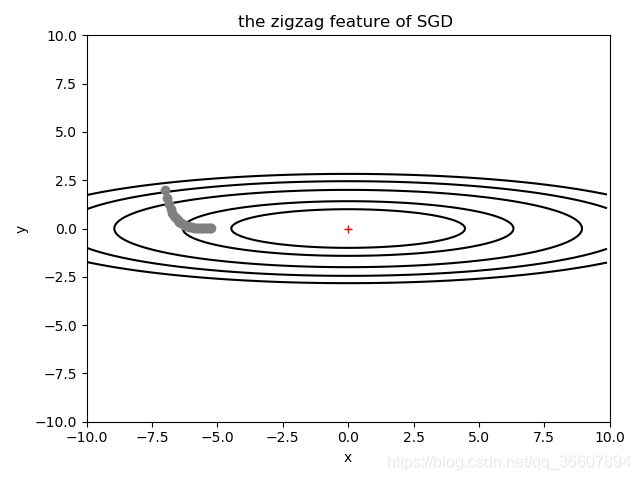
下面对f(x,y)使用梯度下降法,随机选一个初始点(-7,2),展示从初始点到接近原点的梯度下降过程:
这里为了展示SGD对于某些函数会出现之字形下降,故意把学习率设大了,实际上有时候学习率不大,对于某些函数仍有可能出现这种情况:
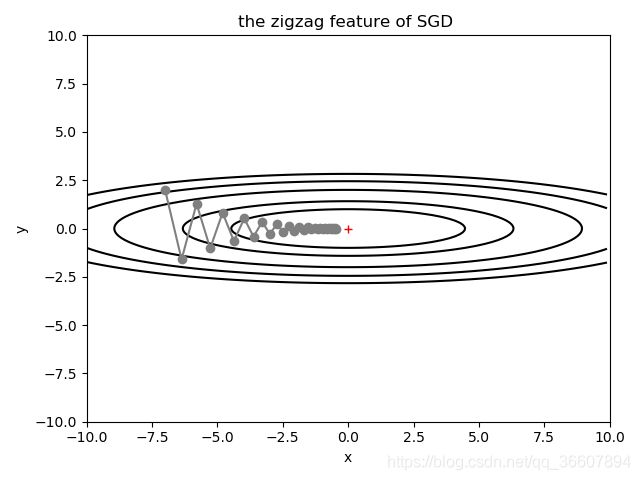
可以看到收敛过程是之字形的,比较慢,但最终还是能收敛到最小值的,但更多更复杂的函数可能就无法收敛到全局最小了。
红色加号标注的是全局最小值坐标(0,0)
画这小破图花了一晚上,各种傻逼或不太傻逼的bug,看到它还是超开心呀
# Zigzag_SGD.py
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return (x[0] ** 2) / 20 + x[1] ** 2
def gradient_descent(f, init_x, lr=0.1, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
# 这里必须用x.copy()
# 否则最终x_history里所有数值都和最后一个数值相同
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
# 把x_history转换为numpy数组
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
temp = x[idx]
x[idx] = temp + h
fxh1 = f(x)
x[idx] = temp - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = temp
return grad
init_x = np.array([-7.0, 2.0]) # 起始点
learning_rate = 0.9 # 学习率较大才会出现之字形震荡下降
stepnum = 30 # 沿着梯度走30步
x, x_history = gradient_descent(func, init_x, lr=learning_rate, step_num=stepnum)
# 画图
plt.figure()
x0 = np.arange(-10.0, 10.0, 0.1)
x1 = np.arange(-10.0, 10.0, 0.1)
X, Y = np.meshgrid(x0, x1)
z = np.array([X, Y])
Z = func(z)
plt.contour(x0, x1, Z, [1,2,4,6,8], colors='black') # 画5条等高线
# 画出30个由梯度下降找到的点
plt.plot(x_history[:, 0], x_history[:, 1], 'o', color='gray')
# 画点间连线
for i in range(x_history.shape[0]-2):
tmp = x_history[i:i+2]
tmp = tmp.T
plt.plot(tmp[0], tmp[1], color='gray')
# 标注原点位置(最小值)
plt.plot(0, 0, '+', color='r')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.xlabel('x')
plt.ylabel('y')
plt.title('the zigzag feature of SGD ')
plt.show()
如果只是把上述代码的学习率改为0.1,那么得到结果如下,没有之字形下降,但由于学习率小,30步只能更新到(-5,0)左右的位置,具体计算值是(-5.17790261e+00, 2.47588008e-03),可以看出y轴方向已经收敛到0了,而x轴由于这个函数自己的特性,会更新很慢,因为整个x轴上的梯度都接近于0,。
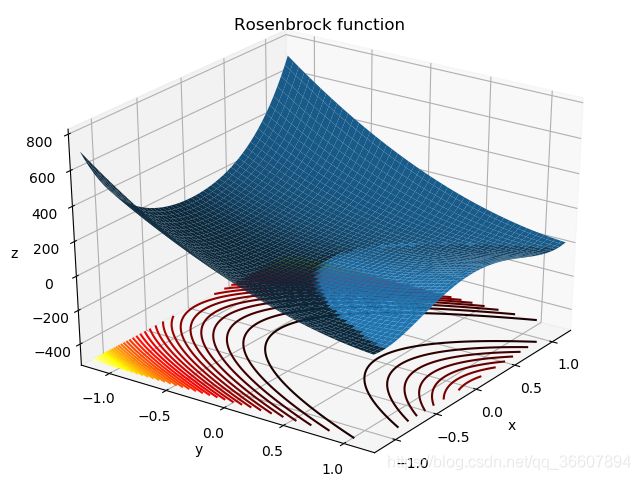
下面用著名的恶意函数——香蕉函数,Rosenbrock函数来试试SGD
函数图像如下,底部画了等高线(蓝色的是我画的,绿色的来自wiki),这里我不明白怎么把y轴翻转过来,画出wiki中的那样,在网上找的代码是
fig = plt.figure()
ax = Axes3D(fig)
ax.xaxis.set_ticks_position('bottom')
ax.invert_xaxis()
ax.yaxis.set_ticks_position('left')
ax.invert_yaxis()
但是经过试验发现这个只适用于二维坐标轴,如下面的等高线和SGD的示意图,在三维坐标系里ax.yaxis.set_ticks_position(‘left’)这行代码会报错,因为会调用库函数axis.py中的第一个set_ticks_position(position)函数,而这个函数并不接受left参数······
然而axis.py中有两个同名同参数的函数,均为set_ticks_position(position),我的代码中ax.xaxis.set_ticks_position(‘bottom’)想调用第一个函数,ax.yaxis.set_ticks_position(‘left’)想要调用第二个函数(允许接收left,right等参数)······
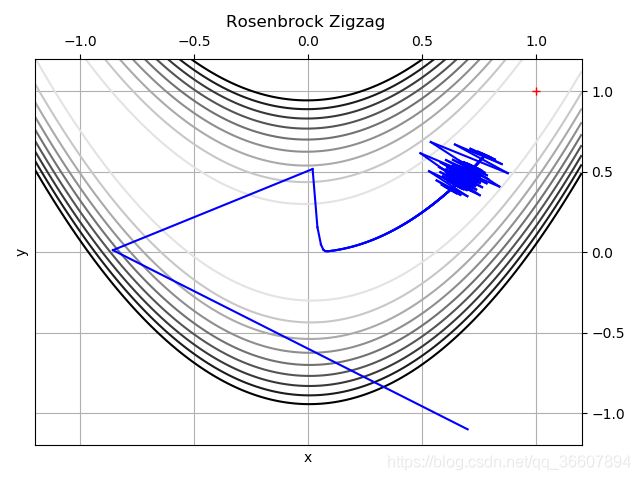
这个函数对超参数的要求很高,我的起点选的已经离最小值点不远了,但是学习率一旦大于0.0035就会出现一次更新就跑到我的画布外面去了·······而且 步数到达1000后面再加多少都是徒劳,还是走不到最小值点·······果然是一个厉害的非凸函数,测试优化最算法的性能杠杠的
代码:
# RosenbrockZigzag.py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Rosenbrock函数
def func(x):
return (1 - x[0]) ** 2 + 100 * (x[1] - x[0]**2) ** 2
def gradient_descent(f, init_x, lr=0.1, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
# 这里必须用x.copy()
# 否则最终x_history里所有数值都和最后一个数值相同
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
# 把x_history转换为numpy数组
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
temp = x[idx]
x[idx] = temp + h
fxh1 = f(x)
x[idx] = temp - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = temp
return grad
init_x = np.array([0.7, -1.1]) # 起始点
learning_rate = 0.0035 # 学习率,再大就会导致一次参数更新跳到非常远的地方
stepnum = 1000 # 沿着梯度走1000步,经过观察,rosenbrock函数走10000步也到不了最小点
# 前面梯度大,一次更新走很远,后面梯度小,几乎没怎么动
x, x_history = gradient_descent(func, init_x, lr=learning_rate, step_num=stepnum)
x = np.linspace(-1.2, 1.2, 200)
y = np.linspace(-1.2, 1.2, 200)
X, Y = np.meshgrid(x, y)
z = np.array([X, Y])
# 画函数图像
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, func(z),alpha=1)
# alpha是透明度
ax.view_init(30, 35)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_zlim (-500, 800)
# 翻转x轴显示方向
ax.xaxis.set_ticks_position('bottom')
ax.invert_xaxis()
plt.title('Rosenbrock function')
# 在函数下方500处画40条等高线
ax.contour(x, y, func(z),40, zdir='z',offset=-500,cmap=plt.cm.hot)
plt.show()
# 画等高线
plt.figure()
plt.contour(x, y, func(z),np.arange(0,100,10), zdir='z', cmap='binary')
# 画所有由梯度下降找到的点
# plt.plot(x_history[:, 0], x_history[:, 1], 'o', color='blue')
# 翻转坐标轴方向
ax = plt.gca()
ax.xaxis.set_ticks_position('top')
ax.invert_xaxis()
ax.yaxis.set_ticks_position('right')
ax.invert_yaxis()
# 画点间连线
for i in range(x_history.shape[0]-2):
tmp = x_history[i:i+2]
tmp = tmp.T
plt.plot(tmp[0], tmp[1], color='blue')
# 标注最小值位置
plt.plot(1, 1, '+', color='r')
plt.xlim(-1.2, 1.2)
plt.ylim(-1.2, 1.2)
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.title('Rosenbrock Zigzag ')
plt.show()