C数学基础专题
数学是程序竞赛中常见的题目,并且很容易和其他题目一起出,作为基础,还是得尽快掌握。
高精度计算
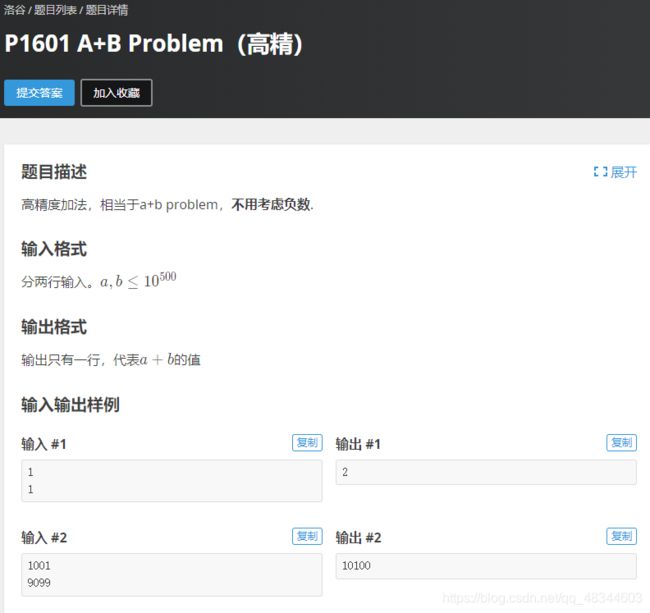
洛谷P1601 A+B高精度
#include
#include
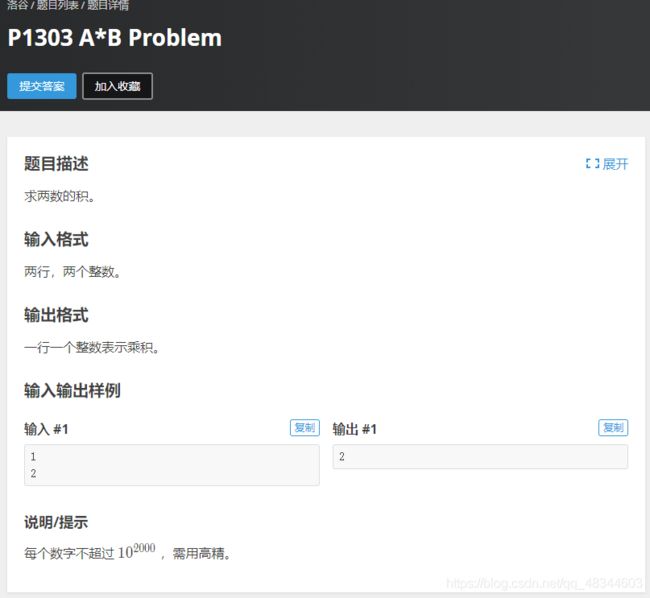
#include 洛谷P1603 A*B高精度
#include
#include
#include 数论
快速幂
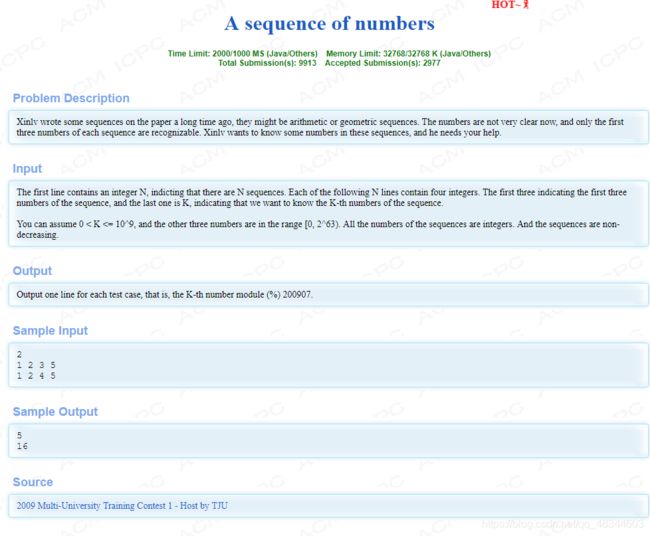
hdu2817 A sequence of numbers
#include
#include
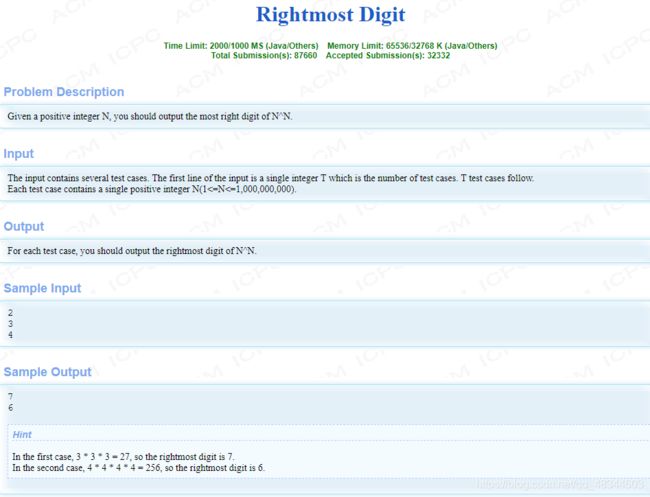
#include hdu1061 Rightmost Digit
#include
#include
#include hdu3117 Fibonacci Numbers
discuss里大佬的博客,证明前4位怎么得到的。http://www.cnblogs.com/WArobot/p/6810504.html
为何可以转为矩阵乘法,因为斐波那契是递归数列,矩阵不像常数,只能表示一个数,矩阵可以记录很多数,比如斐波那契数列,矩阵的00元素记录当前值,01记录前一个值,10和11没用,只是为了方便乘法。然后灵魂就是后面那个递归矩阵,他乘一下就可以代表递归的数运算一下,然后用快速幂。
#include
#include
#include GCD&LCM
gcd:欧几里得算法以及欧几里得算法扩展
欧几里得b站大佬视频:https://www.bilibili.com/video/BV1Ra4y1h723/?spm_id_from=333.788.videocard.0
欧几里得扩展b站大佬视频:https://www.bilibili.com/video/BV1bp4y1S7bW?from=search&seid=6067462148398361649
lcm:两数乘积除去gcd
hdu1019 Least Common Multiple
#include
#include
#include poj1061 青蛙的约会
推荐2篇大佬博客
1.https://blog.csdn.net/swordholy/article/details/4423543
2.https://blog.csdn.net/u011815404/article/details/88423181?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.channel_param
先1后2,慢慢看,对欧几里得扩展会有更深的认识。

#include
#include
#include hdu1576 A/B
上面一题分析透彻,这一题只要自己理清题意,得到等式就可以利用欧几里得扩展了。

#include
#include
#include 乘法逆元&除法取模
hdu5976 Detachment
推荐博客:https://blog.csdn.net/weixin_41707869/article/details/90107418
#include
#include
#include 素数筛选
线性欧拉筛大佬博客:https://www.cnblogs.com/liuwenyao/p/9931230.html
hdu1262 素数对
#include
#include
#include hdu2710 Max Factor
#include
#include
#include hdu3826 Squarefree number
#include
#include
#include 组合数学
鸽巢原理
hdu1205 吃糖果
#include
int main()
{
__int64 n,m,i;
scanf("%I64d",&n);
while(n--)
{
memset(a,0,sizeof(a));
__int64 max=-99;
__int64 sum=0;
scanf("%I64d",&m);
for(i=1;i<=m;i++)
{
scanf("%I64d",&a[i]);
sum+=a[i];
if(a[i]>max)
max=a[i];
}
__int64 sum1=sum+1-max;
if(sum1>=max)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}
hdu1808 Halloween treats
#includehdu5776 sum
#include容斥原理
hdu2841 Visible Trees
#includehdu4135 Co-prime
#include斐波那契数列
hdu3117 Fibonacci Numbers
poj3070 Fibonacci
都是求大数斐波那契数列,hdu3117上面已经写过,用到矩阵快速幂。
母函数
hdu1028 Ignatius and the Princess III
#includehdu1521 排列组合
#include特殊计数
hdu2067 小兔的棋盘(卡特兰数)
#include令h(0)=1,h(1)=1,catalan数满足递推式[1]:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
例如:h(2)=h(0)h(1)+h(1)h(0)=11+11=2
h(3)=h(0)h(2)+h(1)h(1)+h(2)h(0)=12+11+21=5
另类递推式[2]:
h(n)=h(n-1)(4n-2)/(n+1);
递推关系的解为:
h(n)=C(n,2n)*(2n-1) (n=0,1,2,…)
递推关系的另类解为:
h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,…)
hdu4372 Count the Buildings( 斯大林数第一类)
hdu2643 Rank(斯大林数第二类)
#include公平组合游戏
巴什游戏
hdu1846 Brave Game
#include必胜点N必败点P与动态规划
hdu2147 kikis game
#include尼姆游戏
hdu1850 Being a Good Boy in Spring Festival
#includeSG函数
大佬博客:https://www.cnblogs.com/graytido/p/10771907.html
hdu1848 Fibonacci again and again
#include威佐夫游戏
hdu1527 取石子游戏
这里分析奇异局势与非奇异局势的转换。首先奇异局势在这里是P(必败),那么我们处在奇异局势时,必败,我们处在非奇异时,能不能转到奇异局势,见大佬博客:https://blog.csdn.net/Jason_crawford/article/details/52129969?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param
我们可以知道非奇异能够成为奇异,换句话说,因为奇异时P,我们非奇异能变为P,那么我们非奇异就是N(必胜)

#include