caffe参数配置solver.prototxt 及优化算法选择
#caffe参数配置solver.prototxt 及优化算法选择
本文主要包含如下内容:
文章目录
- `solver.prototxt`介绍及流程
- `solver.prototxt`优化算法选择
- 批量梯度下降法(BGD)和 随机梯度下降法(SGD)
- SGD:随机梯度下降法
- AdaGrad:自适应性梯度下降法
- AdaDelta:AdaGrad的扩展
- RMASprop:Adadelta的特例
- Adam:Adaptive Moment Estimation(目前效果最好的梯度下降算法)
- NAG:Nesterov accelerated gradient(加速梯度下降法)
solver.prototxt介绍及流程
参考网址
.proto文件用来定义结构体的参数,.prototxt文件用结构体的初始化数据配置初始化Net
参数配置文件定义了网络模型训练过程中需要设置的参数,如学习率、权重衰减系数、迭代次数、使用GPU还是CPU等。
在前向过程(forward)中计算loss,在反向传播中计算梯度gradient。根据误差度、正则项的梯度以及其他方法的特定项来计算参数更新量。
Solver的流程:
- 设计好需要优化的对象,以及用于学习的训练网络和用于评估的测试网络。(通过调用另外一个配置文件
prototxt来进行) - 通过
forward和backward迭代的进行优化来跟新参数。 - 定期的评价测试网络。 (可设定多少次训练后,进行一次测试)
- 在优化过程中显示模型和
solver的状态
# 设置网络模型,文件的路径要从caffe的根目录开始
net: "examples/mnist/lenet_train_test.prototxt"
# 与test layer中的batch_size结合起来理解,假设样本总数为10000,一次性执行全部数据效率低,因此将测试数据分成几个批次来执行,每个批次的数量就是batch_size。假设batch_size为100,则需要迭代100次才能将10000个数据全部执行完,因此test_iter设置为100.(100*100=10000),合理设置可使得测试遍历完去不测试样本
test_iter: 100
# 训练网络之前不进行测试,默认在训练网络前先进行一次test
test_initialization:false
# 测试间隔,也就是每训练test_interval次,才进行一次测试 ,合理设置可使得训练遍历完全部训练样本
test_interval: 500
# 这个参数乘上train.prototxt中的batch size是你实际使用的batch size。 相当于读取batchsize * itersize个图像才做一下gradient decent。 这个参数可以规避由于gpu内存不足而导致的batchsize的限制 因为你可以用多个iteration做到很大的batch 即使单次batch有限
iter_size: 8
# The base learning rate, momentum and the weight decay of the network.
# base_lr为基础学习率
base_lr: 0.01
# 优化算法选择,此处选择随机梯度下降法(默认为SGD,这一行可以省掉)
type: SGD
# 上一次梯度更新的权重
momentum: 0.9
# 权重衰减项,防止过拟合的一个参数(正则化项)
weight_decay: 0.0005
# The learning rate policy,学习率变化准则
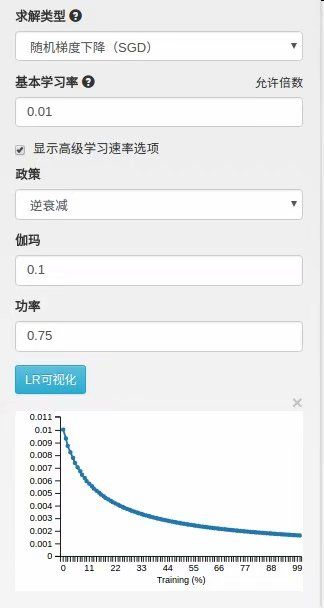
lr_policy: "inv"
# 学习率变化的比率
gamma: 0.0001
power: 0.75
# 每训练display次在屏幕上显示一次
display: 100
# 最大迭代次数,这个数设置太小,会导致没有收敛,精确度很低。设置太大,会导致震荡,浪费时间
max_iter: 10000
# 状态进行保存,snapshot用于设置训练多少次后进行保存,默认为0,不保存。snapshot_prefix 设置保存路径
snapshot: 5000
snapshot_prefix: "examples/mnist/lenet"
# 设置运行模式: CPU or GPU(默认为GPU)
solver_mode: CPU
lr_policy:学习策略
lr_policy可以设置为下面这些值,相应的学习率的计算为:
- fixed: 保持base_lr不变.
- step: 如果设置为step,则还需要设置一个stepsize, 返回 base_lr * gamma ^ (floor(iter / stepsize)),其中iter表示当前的迭代次数
- exp: 返回base_lr * gamma ^ iter, iter为当前迭代次数
- inv: 如果设置为inv,还需要设置一个power, 返回base_lr * (1 + gamma * iter) ^ (- power)
- multistep: 如果设置为multistep,则还需要设置一个stepvalue。这个参数和step很相似,step是均匀等间隔变化,而multistep则是根据stepvalue值变化
- poly: 学习率进行多项式误差, 返回 base_lr (1 - iter/max_iter) ^ (power)
- sigmoid: 学习率进行sigmod衰减,返回 base_lr ( 1/(1 + exp(-gamma * (iter - stepsize))))
solver.prototxt优化算法选择
批量梯度下降法(BGD)和 随机梯度下降法(SGD)
批量梯度下降法(batch gradient descent),是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。(训练集的所有内容)。(容易内存超出,陷入局部最小值)
随机梯度下降法(stochastic gradient descent),这里的随机梯度下降法其实跟MBGD(minibatch gradient descent)是一个意思,即随机抽取一批样本,以此为根据来更新参数。(增加随机性,可以跳出局部最小值)
各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。
对于准确度来说,随机梯度下降法用于仅仅用mini-batch样本决定梯度方向,导致解很有可能不是最优,导致迭代方向变化很大,不能很快的收敛到局部最优解。
同样的,batch size 设置比较大的时候,效果会比较好(不能设置太小或者太大)。在使用GPU的情况下,并且运用矩阵乘法(并行运算),batch size 等于1或10计算一次梯度的时间是一致的。因此:batch size 设置为10的时候,运行速度比batch size 设置为1的时候几乎快10倍。而且。随机性更小,震荡更不明显,加快收敛速度。
SGD:随机梯度下降法
SGD,随机梯度下降法就是每一次迭代计算 mini-batch 的梯度,然后对参数进行更新。利用负梯度和上一次权重的更新值的线性组合(利用传统的梯度下降法容易收敛到局部最优,且选择合适的 learing rate 困难)。学习率a是负梯度的权重。动量u是上一次更新值的权重。
学习参数需要一定的调整才能达到最好的效果。一般的,将学习速率a初始化为0.01,然后在训练中当loss达到稳定时,将a除以一个常数,将这个过程重复多次。对于动量u设置为0.9。u能使权重的更新更为平缓(防抖动),使学习过程更为稳定、快速。
通过交叉验证,动量参数通常设为[0.5,0.9,0.95,0.99]中的一个.有时随着时间而变化,从0.5到0.99;表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,改为0.9。学习率即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。
特征:下降初期时,使用了上一次更新参数,如果下降方向一致,乘上较大的u能够进行很好的加速。下降中后期时,在局部最小值来回震荡的时候,gradient->0,u使得更新幅度增大,从而跳出陷阱。在梯度改变方向的时候,u能够减少更新。总而言之,momentum项能够在相关方向加速SGD,抑制振荡,从而加快收敛。
AdaGrad:自适应性梯度下降法
自适应梯度下降法,对学习率进行了一个约束。即:
特征:前期g_t较小的时候, regularizer较大,能够放大梯度;后期g_t较大的时候,regularizer较小,能够约束梯度;合处理稀疏梯度。
用于平滑的式子eps(一般设为1e-4到1e-8之间)是防止出现除以0的情况。
缺点:仍依赖于人工设置一个全局学习率,学习率设置过大的话,会使regularizer过于敏感,对梯度的调节太大,中后期,分母上梯度平方的累加将会越来越大,使gradient->0,使得训练提前结束。
AdaDelta:AdaGrad的扩展
Adadelta是对Adagrad的扩展。Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。
t%5E2)
特征:训练初中期,加速效果不错,很快;训练后期,反复在局部最小值附近抖动
同时:使用Adadelta算法,我们甚至都无需设置默认的学习率。
E [ Δ θ 2 ] t = γ E [ Δ θ 2 ] t − 1 + ( 1 − γ ) Δ θ t 2 E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2
R M S [ Δ θ ] t = E [ Δ θ 2 ] t + ϵ RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon} RMS[Δθ]t=E[Δθ2]t+ϵ
Δ θ t = − R M S [ Δ θ ] t − 1 R M S [ g ] t g t \Delta \theta_t = - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t} Δθt=−RMS[g]tRMS[Δθ]t−1gt
RMASprop:Adadelta的特例
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
是一个非常高效的适应性学习率方法。这个方法用一种很简单的方式修改了Adagrad
方法,让它不那么激进,单调地降低了学习率。具体说来,就是它使用了一个梯度平方的滑动平均
。
代码中,decay_rate是一个超参数,常用的值是[0.9,0.99,0.999]。RMSProp仍然
是基于梯度的大小来对每个权重的学习率进行修改,这同样效果不错。但是和Adagrad不同,其更
新不会让学习率单调变小,不会发生更新停止的情况。
特征:RMSprop依赖于全局学习率,RMSprop算是Adagrad的一种发展,和Adadelta的变
体,效果趋于二者之间,适合处理非平稳目标对于RNN效果很好。
Adam:Adaptive Moment Estimation(目前效果最好的梯度下降算法)
本质上是带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个
参数的学习率。
特征:结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点,对内存需求较小,为不同的参数计算不同的自适应学习率,也适用于大多非凸优化 - 适用于大数据集和高维空间。
作者建议u1取默认值为0.9,v1为0.999,ϵ为1e-8
NAG:Nesterov accelerated gradient(加速梯度下降法)
Nesterov动量的核心思路是,当参数向量位于某个位置x时,观察上面的动量更新公式可以发现,动量部分会通过mu * v稍微改变参数向量。因此,计算x + mu * v的梯度而不是“旧”位置x的梯度就有意义了。Nesterov项在梯度更新时做一个校正,避免前进太快,同时提高灵敏度。 关键:计算梯度的位置不一样.
![]()
Momentum项和Nesterov项都是为了使梯度更新更加灵活,对不同情况有针对性。