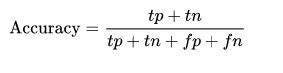准确率(正确率, accuracy),精确度(precision), 召回率(recall) 都是计算正条件值 (Condition positive, 正样本).
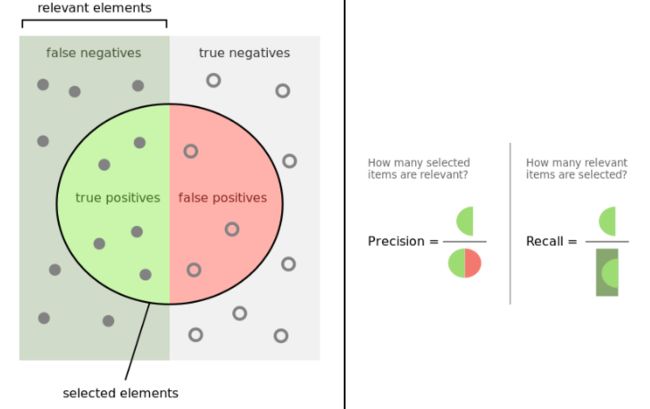
查准率(Precision)查准率反映了被判定为正例中真正的正例样本的比重
查全率(Recall)查全率反映了被判定的正例占总的正例的比重
100次地震预测, 实际10次地震,TP为10, RECALL为1 , 预测很全
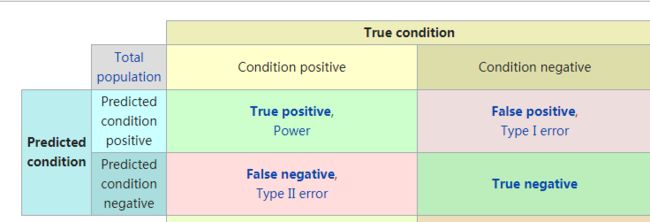
显然,混淆矩阵包含四部分的信息:
- True negative(TN),称为真阴率,表明实际是负样本预测成负样本的样本数
- False positive(FP),称为假阳率,表明实际是负样本预测成正样本的样本数
- False negative(FN),称为假阴率,表明实际是正样本预测成负样本的样本数
- True positive(TP),称为真阳率,表明实际是正样本预测成正样本的样本数
对照着混淆矩阵,很容易就能把关系、概念理清楚,但是久而久之,也很容易忘记概念。不妨我们按照位置前后分为两部分记忆,前面的部分是True/False表示真假,即代表着预测的正确性,后面的部分是positive/negative表示正负样本,即代表着预测的结果,所以,混淆矩阵即可表示为正确性-预测结果的集合。现在我们再来看上述四个部分的概念(均代表样本数,下述省略):
- TN,预测是负样本,预测对了
- FP,预测是正样本,预测错了
- FN,预测是负样本,预测错了
- TP,预测是正样本,预测对了
几乎我所知道的所有评价指标,都是建立在混淆矩阵基础上的,包括准确率、精准率、召回率、F1-score,当然也包括AUC。
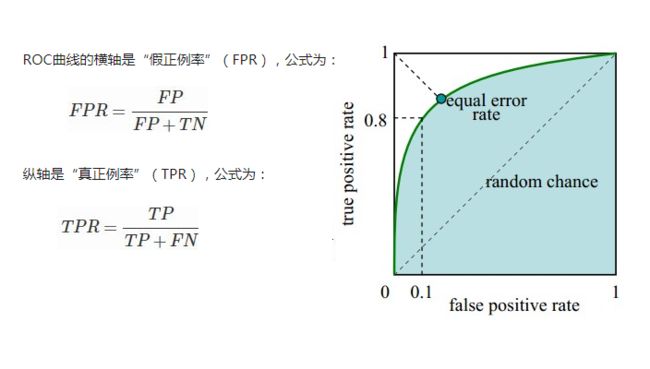
对于真正例率TPR,分子是得分>t里面正样本的数目,分母是总的正样本数目。 而对于假正例率FPR,分子是得分>t里面负样本的数目,分母是总的负样本数目.
这里是归一化思想, 即各类的预测效果如何。TPR,正样本预对OK率;FPR,负样本预对FAIL率;
引用 : https://www.zybuluo.com/frank-shaw/note/152851
假设有下面两个分类器,哪个好?(样本中有A类样本90个,B 类样本10个。)
| 、 | A类样本 | B类样本 | 分类精度 |
|---|---|---|---|
| 分类器C1 | A*90(100%) | A*10(0%) | 90% |
| 分类器C2 | A*70 + B*20 (78%) | A*5 + B*5 (50%) | 75% |
可以代入到上面的两个分类器当中,可以得到下面的表格(分类器C1):
| 、 | 预测A | 预测B | 合计 |
|---|---|---|---|
| 实际A | 90 | 0 | 90 |
| 实际B | 10 | 0 | 10 |
TPR = FPR = 1.0.
分类器C2:
| 、 | 预测A | 预测B | 合计 |
|---|---|---|---|
| 实际A | 70 | 20 | 90 |
| 实际B | 5 | 5 | 10 |
TPR = 0.78, FPR = 0.5
那么,以TPR为纵坐标,FPR为横坐标画图,可以得到:
上图中蓝色表示C1分类器,绿色表示C2分类器。可以知道,这个时候绿色的点比较靠近左上角,可以看做是分类效果较好。所以评估标准改为离左上角近的是好的分类器(考虑了正负样本的综合分类能力)。
一连串这样的点构成了一条曲线,该曲线就是ROC曲线。而ROC曲线下的面积就是AUC(Area under the curve of ROC)。这就是AUC指标的由来。
如何画ROC曲线
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值才能得到这样的曲线,这又是如何得到的呢?
可以通过分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本),来动态调整一个样本是否属于正负样本(还记得当时阿里比赛的时候有一个表示被判定为正样本的概率的列么?)
或者
但仍有一个问题,对于一个学习器它的预测结果只能产生一对(FPR,TPR),这只能绘制一个点,不足以绘制出一条曲线。实际上对于许多学习器在判定二分类问题时是预测出一个对于真值的范围在[0.0, 1.0]之间的概率值,而判定是否为真值则看该概率值是否大于设定的阈值(Threshold)。例如如果阈值设定为0.5则所有概率值大于0.5的均为正例,其余为反例。因此对于不同的阈值我们可以得到一系列相应的FPR和TPR,从而绘制出ROC曲线。
以下列数据举例:
y_true = [0, 1, 0, 1],真实值
y_score = [0.1, 0.35, 0.4, 0.8], 预测概率值 ??? 如果预测值与真值一样呢? ROC会是什么样?
分别取4组判定正例用的阈值(大于等于):[0.1, 0.35, 0.4, 0.8],可得相应4组FPR,TPR:
FPR: [1, 0.5, 0.5, 0]
TPR: [1, 1, 0.5, 0.5]
其中
|
|
|
|
绘制ROC曲线图如下: ![]()
ROC曲线所覆盖的面积称为AUC(Area Under Curve),可以更直观的判断学习器的性能,AUC越大则性能越好。对于该例的AUC值为0.75
AUC(Area under the Curve of ROC)是ROC曲线下方的面积,是判断二分类预测模型优劣的标准。ROC(receiver operating characteristic curve)接收者操作特征曲线,是由二战中的电子工程师和雷达工程师发明用来侦测战场上敌军载具(飞机、船舰)的指标,属于信号检测理论。ROC曲线的横坐标是伪阳性率(也叫假正类率,False Positive Rate),纵坐标是真阳性率(真正类率,True Positive Rate)
显然,ROC曲线的横纵坐标都在[0,1]之间,自然ROC曲线的面积不大于1。现在我们来分析几个特殊情况,从而更好地掌握ROC曲线的性质:
- (0,0):假阳率和真阳率都为0,即分类器全部预测成负样本
- (0,1):假阳率为0,真阳率为1,全部完美预测正确,happy
- (1,0):假阳率为1,真阳率为0,全部完美预测错误,悲剧
- (1,1):假阳率和真阳率都为1,即分类器全部预测成正样本
- TPR=FPR,斜对角线,预测为正样本的结果一半是对的,一半是错的,代表随机分类器的预测效果
于是,我们可以得到基本的结论:ROC曲线在斜对角线以下,则表示该分类器效果差于随机分类器,反之,效果好于随机分类器,当然,我们希望ROC曲线尽量除于斜对角线以上,也就是向左上角(0,1)凸。
AUC(Area under the ROC curve)
ROC曲线一定程度上可以反映分类器的分类效果,但是不够直观,我们希望有这么一个指标,如果这个指标越大越好,越小越差,于是,就有了AUC。AUC实际上就是ROC曲线下的面积。AUC直观地反映了ROC曲线表达的分类能力。
- AUC = 1,代表完美分类器
- 0.5 < AUC < 1,优于随机分类器
- 0 < AUC < 0.5,差于随机分类器
AUC能拿来干什么
从作者有限的经历来说,AUC最大的应用应该就是点击率预估(CTR)的离线评估。CTR的离线评估在公司的技术流程中占有很重要的地位,一般来说,ABTest和转全观察的资源成本比较大,所以,一个合适的离线评价可以节省很多时间、人力、资源成本。那么,为什么AUC可以用来评价CTR呢?我们首先要清楚两个事情:
- CTR是把分类器输出的概率当做是点击率的预估值,如业界常用的LR模型,利用sigmoid函数将特征输入与概率输出联系起来,这个输出的概率就是点击率的预估值。内容的召回往往是根据CTR的排序而决定的。
- AUC量化了ROC曲线表达的分类能力。这种分类能力是与概率、阈值紧密相关的,分类能力越好(AUC越大),那么输出概率越合理,排序的结果越合理。
我们不仅希望分类器给出是否点击的分类信息,更需要分类器给出准确的概率值,作为排序的依据。所以,这里的AUC就直观地反映了CTR的准确性(也就是CTR的排序能力)