gdtop818

DANN：Unsupervised Domain Adaptation by Backpropagation

本篇是迁移学习专栏介绍的第十三篇论文，发表在ICML15上。论文提出了用对抗的思想进行domain adaptation，该方法名叫DANN(或RevGrad)。核心的问题是同时学习分类器、特征提取器、以及领域判别器。通过最小化分类器误差，最大化判别器误差，使得学习到的特征表达具有跨领域不变性。

Abstract

高性能的深层体系结构是针对大量标记数据进行训练的。在缺少特定任务的标记数据的情况下，域自适应通常提供了一个有吸引力的选项，因为具有类似性质但来自不同域的标记数据(例如合成图像)是可用的。在此，我们提出了一种在深层体系结构中进行域自适应的新方法，该方法可以训练来自源域的大量标记数据和来自目标域的大量未标记数据(不需要标记的target domain数据)。

随着训练的进行，该方法促进了

对源域上的主要学习任务具有鉴别性的深层特征的出现
关于域之间的迁移具有不变性

我们证明，这种自适应行为几乎可以在任何前馈模型中实现，通过增加几个标准层和一个简单的新的梯度逆转层。生成的增强体系结构可以使用标准的反向传播进行训练。

总的来说，使用任何深度学习包都可以轻松地实现该方法。该方法在一系列的图像分类实验中取得了良好的效果，在存在较大的域迁移的情况下，取得了较好的自适应效果，在Office数据集上的性能优于以往的先进方法。

1. Introduction

深度前馈体系结构为各种机器学习任务和应用程序带来了令人印象深刻的最新进展。然而，目前，只有在有大量标记的训练数据可用时，才能实现这些性能飞跃。同时，对于缺少标记数据的问题，仍然有可能获得足够大的训练集来训练大规模的深度模型，但是这些训练集的数据分布与测试时遇到的实际数据发生了变化。一个特别重要的例子是合成的或半合成的训练数据，这些数据可能非常丰富，并且被完全标记，但是它们不可避免地具有与真实数据不同的分布(Liebelt & Schmid, 2010; Stark et al., 2010; Vazquez et al. , 2014; Sun & Saenko, 2014)。

在训练分布和测试分布之间存在迁移的情况下学习判别分类器或其他预测器被称为域适应(DA)。在浅层学习的背景下，已经提出了一些领域适应的方法，例如在给定和固定了数据表示/特征的情况下。然后，这些方法构建源(训练时间)域和目标(测试时间)域之间的映射，这样，当使用域之间的学习映射组合时，为源域学习的分类器也可以应用于目标域。域适应方法的吸引力在于，当目标域数据要么完全无标记(无监督域注释)，要么标记样本很少(半监督域适应)时，能够学习域之间的映射。下面，我们将重点讨论较难的无监督情况，尽管所提出的方法可以相当直接地推广到半监督情况。

与以往大多数使用固定特征表示的领域适应相关论文不同，我们侧重于将领域适应和深度特征学习结合在一个训练过程中(深度领域适应)。我们的目标是将领域自适应嵌入到学习表示的过程中，使最终的分类决策基于对领域变化既具有区别性又不变性的特征，即在源域和目标域中具有相同或非常相似的分布。这样，得到的前馈网络可以应用于目标域，而不受两个域之间位移的影响。

因此，我们关注结合(i)辨别力和(ii)领域不变性的学习特性。这是通过联合优化基础特性以及对这些特性进行操作的两个判别分类器来实现的：(i)用于预测类标签的标签预测器，在训练期间和测试时都使用域分类器，用于在训练过程中区分源域和目标域。对分类器参数进行优化，使其在训练集上的误差最小；对底层深度特征映射参数进行优化，使标签分类器的损失最小，使域分类器的损失最大。后者鼓励在优化过程中出现域不变的特性。

DANN：Unsupervised Domain Adaptation by Backpropagation_第1张图片

图1所示。该结构包括一个深特征提取器(绿色)和一个深标签预测器(蓝色)，它们共同构成一个标准的前馈结构。在基于反向传播的训练过程中，通过梯度反转层将梯度乘以一定的负常数，将一个域分类器(红色)连接到特征提取器，实现无监督域自适应。否则，训练将以标准的方式进行，并最小化标签预测损失(对于源示例)和域分类损失(对于所有示例)。梯度反转确保了两个域上的特征分布是相似的(对于域分类器来说，尽可能难以区分)，从而产生域不变的特征。

关键的是，我们证明了这三个训练过程都可以嵌入到一个适当组成的使用标准层和损失函数的深度前馈网络中(图1)，并且可以使用基于随机梯度下降或其修改的标准反向传播算法(例如带动量的SGD)进行训练。我们的方法是通用的，因为它可以用于向任何可以通过反向传播训练的现有前馈体系结构添加域适配。实际上，所提议的体系结构的唯一非标准组件是一个相当简单的梯度反转层，它在正向传播期间保持输入不变，并在反向传播期间通过将其乘以一个负标量来反转梯度。

下面，我们详细的建议方法领域适应深架构，传统的深度学习和现在的结果图像数据集(如MNISTT (LeCun et al., 1998)和SVHN(Netzer et al., 2011))以及OFFICE benchmarks (Saenko et al., 2010)，在该方法的精度比以往大大提高。

2. Related work

近年来，人们提出了大量的领域自适应方法，这里我们将重点介绍相关的领域自适应方法。多种方法通过匹配源域和目标域的特征分布来实现无监督域自适应。有些方法通过重新权衡或从源域中选择样本来实现这一点(Borgwardt et al., 2006; Huang et al., 2006; Gong et al., 2013)；而其他人则寻求一种明确的特征空间转换，将源分布映射到目标分布(Pan et al., 2011; Gopalan et al., 2011; Baktashmotlagh et al., 2013)。分布匹配方法的一个重要方面是度量分布之间相似性的方法。在这里，一个流行的选择是匹配核再生希尔伯特空间中的分布方式 (Borgwardt et al., 2006; Huang et al., 2006)，而(Gong et al., 2012; Fernando et al., 2013)绘制与每个分布相关的主轴。我们的方法也尝试匹配特征空间分布，但是这是通过修改特征表示本身来实现的，而不是通过重新加权或几何变换。此外，我们的方法(隐式地)使用了一种非常不同的方法来测量分布之间的差异，该方法基于分布的可分性，采用了一种经过深度判别训练的分类器。

有几种方法从源领域逐渐过渡到目标领域(Gopalan et al., 2011; Gong et al., 2012)通过训练分布的逐步变化。在这些方法中(S. Chopra & Gopalan, 2013)通过对一系列深层自动编码器进行分层训练，逐步将源域样本替换为目标域样本，实现了这一目标。相对于(Glorot et al.， 2011)的类似方法，这种方法只需要为两个域训练一个深层的自动编码器，这是一种改进。在这两种方法中，实际的分类器/预测器都是使用自动编码器学习的特征表示在单独的步骤中学习的。与(Glorot et al., 2011; S. Chopra & Gopalan, 2013)，我们的方法在统一的体系结构中，使用单一的学习算法(反向传播)，共同进行特征学习、领域自适应和分类器学习。因此，我们认为我们的方法更简单(无论是在概念上还是在实现上)。我们的方法在流行的OFFICE基准测试上也取得了相当好的结果。虽然上述方法执行无监督域自适应，但也有一些方法通过利用目标域的标记数据来执行监督域自适应。在深度前馈体系结构的上下文中，这些数据可用于对源域(Zeiler & Fergus, 2013; Oquab et al., 2014; Babenko et al., 2014)。我们的方法不需要标记目标域数据。同时，它可以很容易地在可用时合并这些数据。(Goodfellow et al., 2014)描述了一个与我们相关的想法。虽然他们的目标是完全不同(建筑生成深层网络,可以合成样品),他们测量的方式,减少训练数据的分布之间的差异和合成数据的分布非常类似于我们的架构方式措施和最小化两个域之间的差异特征分布。

最后，(Tzeng et al., 2014)最近的一份并发报告也关注了前馈网络中的域适应。他们的技术集度量并最小化跨域数据手段的距离。这种方法可以看作是我们的方法的一阶近似，它寻求分布之间更紧密的对齐。

3. Deep Domain Adaptation

3.1. The model

现在，我们详细介绍了所提出的领域适应模型。我们假设模型适用于输入样本 $\mathbf{x} \in X$ ，其中是某个输入空间和来自标签空间的某些标签(输出)y。下面，我们假设分类问题中Y是一个有限集 $(Y=\{1,2, \ldots L\})$ ，但是我们的方法是通用的，可以处理其他深度提要的任何输出标签空间正向模型可以处理。我们进一步假设在 $X \otimes Y$ 上存在两个分布 $\mathcal{S}(x, y) \text { and } \mathcal{T}(x, y)$ ，分别称为源分布和目标分布(或源域和目标域)。这两种分布都假定为复杂和未知的，而且相似但不同(换句话说， $\mathcal{S}$ 从 $\mathcal{T}$ 移到某个域上)。

我们的最终目标是能够预测标签y给定目标分布的输入x。在训练时，我们可以访问大量的训练样本 $\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \dots, \mathbf{x}_{N}\right\}$ 来自源和目标域的分布式根据边际分布 $\mathcal{S}(\mathbf{x}) \text { and } \mathcal{T}(\mathbf{x})$ 我们与di表示二进制变量(域标签)i的例子，这表明是否xi来自源分布 $\left(\mathbf{x}_{i} \sim \mathcal{S}(\mathbf{x}) \text { if } d_{i}=0\right)$ 或从目标分布 $\left(\mathbf{x}_{i} \sim \mathcal{T}(\mathbf{x}) \text { if } d_{i}=1\right)$ 。对于源分布( $d_{i}=0$ )中的示例，在训练时已知对应的标签 $y_{i} \in Y$ 。对于来自目标域的示例，我们不知道训练时的标签，我们希望在测试时预测这些标签。

现在，我们定义了一个深度前馈体系结构，对于每个输入x，它预测其标签y和域标签 $d \in\{0,1\}$ 。我们将这种映射分解为三个部分。我们假设输入x是第一次由一个映射映射 $G_{f}$ (特征提取器)采用特征向量 $\mathbf{f} \in \mathbb{R}^{D}$ 。功能映射可能还包括几层前馈和我们表示向量的参数 $\theta_{f}$ 所有层的映射，即 $\mathbf{f}=G_{f}\left(\mathbf{x} ; \theta_{f}\right)$ 。然后,特征向量f是由一个映射映射 $G_{y}$ 标签(标签预测)y，和我们与 $\theta_{y}$ 表示这种映射的参数。最后，映射到相同的特征向量f域标签d由一个映射 $G_{d}$ (域分类器)参数(图1)。

在学习阶段，我们的目标是最小化预测损失的标签带注释的一部分(即源部分)的训练集和特征提取器和标签的参数预测因此优化以减少源领域的经验损失样品。这保证了特征f的鉴别性，保证了特征提取器和标签预测器在源域上的组合具有良好的整体预测性能。

同时，我们希望使特性f域不变。也就是说，我们想让分布 $S(\mathbf{f})=\left\{G_{f}\left(\mathbf{x} ; \theta_{f}\right) | \mathbf{x} \sim S(\mathbf{x})\right\}$ 和 $T(\mathbf{f})=\left\{G_{f}\left(\mathbf{x} ; \theta_{f}\right) | \mathbf{x} \sim T(\mathbf{x})\right\}$ 是相似的。在协变量移位假设下，这将使目标域上的标签预测精度与源域上的相同(Shimodaira, 2000)。然而，测量分布 $S(\mathbf{f}) \text { and } T(\mathbf{f})$ 的不同之处并不简单，因为f是高维的，而且分布本身随着学习的进展而不断变化。估计不同的一种方法是看域分类器 $G_{d}$ 的损失，提供的参数θd域分类器的训练来区分这两个特性分布以最优的方式。

这一观察结果引出了我们的想法。在训练时，为了获得域不变特性，我们寻求参数 $\theta_{f}$ 最大化的功能映射域分类器的损失(通过两个特性分布尽可能相似)，同时寻求域分类器的参数 $\theta_{d}$ 域分类器的损失最小化。此外，我们寻求最小化标签预测器的损失。

更正式地说，我们考虑功能：

$\begin{array}{c}{E\left(\theta_{f}, \theta_{y}, \theta_{d}\right)=\sum_{i=1, N \atop \overline{d}_{i}=N} L_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right)-} \\ {\lambda \sum_{i=1 . N} L_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{d}\right), y_{i}\right)}\end{array}$

$=\sum_{i=1 \ldots N \atop d_{i}=0} L_{y}^{i}\left(\theta_{f}, \theta_{y}\right)-\lambda \sum_{i=1 . . . N} L_{d}^{i}\left(\theta_{f}, \theta_{d}\right)$

其中， $L_{y}(\cdot, \cdot)$ 为标签预测的损失(如多项)， $L_{d}(\cdot, \cdot)$ 为域分类的损失(如logistic)，而 $L_{y}^{i} \text { and } L_{d}^{i}$ 表示第i个训练示例中评估的相应损失函数。根据我们的想法，我们正在寻求参数 $\hat{\theta}_{f}, \hat{\theta}_{y}, \hat{\theta}_{d}$ ，交付一个鞍点的功能(1)

$\begin{array}{c}{\left(\hat{\theta}_{f}, \hat{\theta}_{y}\right)=\arg \min _{\theta_{f}, \theta_{y}} E\left(\theta_{f}, \theta_{y}, \hat{\theta}_{d}\right)} \\ {\hat{\theta}_{d}=\arg \max _{\theta_{d}} E\left(\hat{\theta}_{f}, \hat{\theta}_{y}, \theta_{d}\right)}\end{array}$

在鞍点处，域分类器的参数 $\theta_{d}$ 最小化域分类损失(因为它进入(1)负号)的参数 $\theta_{y}$ 标签预测减少标签预测损失。特征映射参数 $\theta_{f}$ 最小化标签预测损失(即功能是区别的)，而最大化域分类损失(即功能域不变)。参数λ控制两个目标之间的权衡，形状特征在学习。下面，我们证明了标准随机梯度求解器(SGD)可用于鞍点(2)-(3)的搜索。

3.2. Optimization with backpropagation

鞍点(2)-(3)可以作为后续随机更新的一个固定点：

$\begin{array}{c}{\theta_{f} \longleftarrow \theta_{f}-\mu\left(\frac{\partial L_{y}^{i}}{\partial \theta_{f}}-\lambda \frac{\partial L_{d}^{i}}{\partial \theta_{f}}\right)} \\ {\theta_{y} \longleftarrow \theta_{y}-\mu \frac{\partial L_{y}^{i}}{\partial \theta_{y}}} \\ {\theta_{d} \longleftarrow \theta_{d}-\mu \frac{\partial L_{d}^{i}}{\partial \theta_{d}}}\end{array}$

哪里是学习率(可能随时间而变化)。更新(4)-(6)非常类似于前馈深度模型的随机梯度下降(SGD)更新，该模型由特征提取器输入标签预测器和区域分类器。(4)的区别是λ因子(区别很重要，因为没有这样的因子，随机梯度下降法试图使特征在不同区域间不相似，从而使区域分类损失最小化)。虽然直接实现(4)-(6)作为SGD是不可能的，但我们非常希望将更新(4)-(6)减少到某种形式的SGD，因为SGD(及其变体)是大多数用于深度学习的包中实现的主要学习算法。

幸运的是，可以通过引入定义如下的特殊梯度反转层(GRL)来实现这种缩减。梯度逆转层没有与之关联的参数(除了meta-parameter λ，不通过反向传播更新)。在正向传播过程中，GRL作为一个恒等变换。在反向传播，GRL梯度从随后的水平，增加了λ和将其传递给前面的层。使用现有的面向对象包实现这样的层来进行深度学习非常简单，比如为前向支持(标识转换)、后向支持(乘以常量)和参数更新(没什么)定义过程非常简单。

上面定义的GRL插入到特征提取器和域分类器之间，得到图1所示的体系结构。反向传播过程通过GRL,下游的偏导数的损失GRL (Ld) w.r.t.上游的GRL层参数(即 $\theta_{f}$ )乘以-λ，例如 $\frac{\partial L_{d}}{\partial \theta_{f}}$ 实际上是 $-\lambda \frac{\partial L_{d}}{\partial \theta_{f}}$ 所取代。因此,运行SGD在生成的模型实现了更新(4)-(6)和(1)的收敛于一个鞍点。在数学上，我们可以正式将梯度逆转层视为伪函数 $R_{\lambda}(\mathbf{x})$ 定义为两个(不相容)方程描述其向前和反向传播：

$\begin{array}{c}{R_{\lambda}(\mathbf{x})=\mathbf{x}} \\ {\frac{d R_{\lambda}}{d \mathbf{x}}=-\lambda \mathbf{I}}\end{array}$

其中I是一个单位矩阵。我们可以定义的客观“伪函数” $\left(\theta_{f}, \theta_{y}, \theta_{d}\right)$ 内被随机梯度下降优化我们的方法：

$\begin{array}{c}{\tilde{E}\left(\theta_{f}, \theta_{y}, \theta_{d}\right)=\sum_{i=1 . N \atop \overline{d}_{i}=N} L_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right)+} \\ {\sum_{i=1 . N} L_{d}\left(G_{d}\left(R_{\lambda}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right)\right) ; \theta_{d}\right), y_{i}\right)}\end{array}$

运行更新(4)-(6)可以实现为(9)做SGD，并导致同时出现域不变和有区别的特性。学习后，标签预测因子 $y(\mathbf{x})=G_{y}\left(G_{f}\left(\mathbf{x} ; \theta_{f}\right) ; \theta_{y}\right)$ 可以用来预测标签样本目标域(以及从源域)。

面概述的简单学习过程可以按照(Goodfellow et al., 2014)中的建议重新推导/概括(见附录A)。

3.3. Relation to 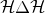$\mathcal{H} \Delta \mathcal{H}$ -distance

在本节中，我们从 $\mathcal{H} \Delta \mathcal{H}$ 距离的角度简要分析了我们的方法(Ben-David et al., 2010; Cortes & Mohri, 2011)，在非保守域适应理论中得到了广泛的应用。正式，

$\begin{array}{r}{d_{\mathcal{H} \Delta \mathcal{H}}(\mathcal{S}, \mathcal{T})=2 \sup _{h_{1}, h_{2} \in \mathcal{H}}\left|P_{\mathbf{f} \sim \mathcal{S}}\left[h_{1}(\mathbf{f}) \neq h_{2}(\mathbf{f})\right]-\right.} \\ {-P_{\mathbf{f} \sim \mathcal{T}}\left[h_{1}(\mathbf{f}) \neq h_{2}(\mathbf{f})\right] |}\end{array}$

定义了两个分布之间的差异距离 $\mathcal{S}$ 和 w.r.t.假设集h .使用这个概念可以获得概率约束(Ben-David et al., 2010)的性能 $\varepsilon_{\mathcal{T}}(h)$ 的一些分类器h 评估目标领域由于其性能 $\varepsilon_{\mathcal{S}}(h)$ 源域：

$\varepsilon_{\mathcal{T}}(h) \leq \varepsilon_{\mathcal{S}}(h)+\frac{1}{2} d_{\mathcal{H} \Delta \mathcal{H}}(\mathcal{S}, \mathcal{T})+C$

其中 $\mathcal{S}$ 和分别是源分布和目标分布，不依赖于特定的h。

在特征提取器 $G_{f}$ 和一组标签预测器 $\mathcal{H}_{p}$ 生成的表示空间上考虑固定的 $\mathcal{S}$ 和。我们假设域分类器 $\mathcal{H}_{d}$ 族足够丰富，可以包含 $\mathcal{H}_{p}$ 的对称差分假设集：

$\mathcal{H}_{p} \Delta \mathcal{H}_{p}=\left\{h | h=h_{1} \oplus h_{2}, h_{1}, h_{2} \in \mathcal{H}_{p}\right\}$

这并不是一个不切实际的假设，因为我们可以自由选择我们想要的 $\mathcal{H}_{d}$ 。例如，我们可以将域鉴别器的体系结构设置为标签预测器的两个副本逐层串联，然后是一个旨在学习or函数的两层非线性感知器。假设成立，可以很容易地看出， $G_{d}$ 的训练与 $d_{\mathcal{H}_{p} \Delta \mathcal{H}_{p}}(\mathcal{S}, \mathcal{T})$ 的估计密切相关。事实上，

$\begin{array}{l}{d_{\mathcal{H}_{p} \Delta \mathcal{H}_{p}}(\mathcal{S}, \mathcal{T})=} \\ {\quad=2 \sup _{h \in \mathcal{H}_{p} \Delta \mathcal{H}_{p}}\left|P_{\mathrm{f} \sim \mathcal{S}}[h(\mathrm{f})=1]-P_{\mathrm{f} \sim \mathcal{T}}[h(\mathrm{f})=1]\right| }\end{array}$

$\begin{array}{l}{ \leq 2 \sup _{h \in \mathcal{H}_{d}}\left|P_{\mathrm{f} \sim \mathcal{S}}[h(\mathrm{f})=1]-P_{\mathrm{f} \sim \mathcal{T}}[h(\mathrm{f})=1]\right|=} \\ {=2 \sup _{h \in \mathcal{H}_{d}}|1-\alpha(h)|=2 \sup _{h \in \mathcal{H}_{d}}[\alpha(h)-1]}\end{array}$

在 $\alpha(h)=P_{\mathrm{f} \sim \mathcal{S}}[h(\mathbf{f})=0]+P_{\mathrm{f} \sim \mathcal{T}}[h(\mathbf{f})=1]$ 是最大化的最佳 $G_{d}$ 。

因此，最优判别器给出了的上界 $d_{\mathcal{H}_{p} \Delta \mathcal{H}_{p}}(\mathcal{S}, \mathcal{T})$ 。逆转的同时，反向传播梯度变化表示空间，使 $\alpha\left(G_{d}\right)$ 成为小有效地减少设计 $d_{\mathcal{H}_{p} \Delta \mathcal{H}_{p}}(\mathcal{S}, \mathcal{T})$ ，导致更好的近似 $\varepsilon_{\mathcal{T}}\left(G_{y}\right) \text { by } \varepsilon_{\mathcal{S}}\left(G_{y}\right)$ 。

4. Experiments

我们对一些流行的图像数据集及其修改进行了广泛的评估。其中包括深受深度学习方法欢迎的小图像的大规模数据集，以及OFFICE数据集(Saenko et al., 2010)，后者实际上是计算机视觉领域适应的标准，但图像要少得多。

Baselines. 对于大多数实验，评估以下基线。只训练源模型而不考虑目标域数据(网络中没有包含域分类器分支)。训练-目标模型在目标域上训练，显示类标签。该模型是DA方法的一个上界，假设目标数据是丰富的，并且域之间的移动是相当大的。

此外，我们将我们的方法与最近提出的基于子空间对齐(SA)的无监督DA方法进行了比较(Fernando et al.， 2013)，该方法在新数据集上易于设置和测试，但在与其他浅层DA方法的实验比较中也表现得很好。为了提高这个基线的性能，我们从{2，…，60}使目标域上的测试性能最大化。为了在我们的设置中应用SA，我们训练了一个只包含源的模型，然后考虑标签预测器(在最终的线性分类器之前)中最后一个隐藏层的激活作为描述符/特征，并学习源和目标域之间的映射(Fernando et al.， 2013)。

因为SA基线需要训练新的分类器适应特性后，为了把所有的平等设置相比，我们重新训练的最后一层标签使用标准线性支持向量机预测(Fan et al., 2008)为所有四种考虑方法(包括我们的再训练后，目标域的性能基本保持不变)。

对于OFFICE数据集(Saenko et al.， 2010)，我们使用以前发表的结果直接比较了我们的全网络(特征提取器和标签预测器)与最近DA方法的性能。

CNN architectures. 一般来说，我们从两个或三个卷积层组成特征提取器，从以前的工作中选择它们的精确配置。我们在附录b中给出了准确的体系结构。对于域适配器，我们坚持使用三个完全连接的层 $(x \rightarrow 1024 \rightarrow 1024 \rightarrow 2)$ ，但是MNIST使用了一个更简单的 $(x \rightarrow 100 \rightarrow 2)$ 结构来加速实验。·

对于损失函数，我们将 $L_{y} \text { and } L_{d}$ 分别设为logistic回归损失和二项式交叉熵

CNN training procedure. 该模型在128个批次上进行了训练。图像经过平均减法预处理。每个批处理的一半由来自源域的示例填充(使用已知标签)，其余由目标域(使用未知标签)组成。为了抑制噪声信号域分类器的训练过程的早期阶段,而不是修复适应因子λ,我们逐渐改变它从0到1使用下面的时间表：

$\lambda_{p}=\frac{2}{1+\exp (-\gamma \cdot p)}-1$

Visualizations. 我们使用t-SNE (van der Maaten, 2013)投影可视化功能分布在不同的网络,而使用彩色编码域(图3)。我们观察强大的通信之间的成功改编的分类精度为目标域和之间的重叠域分布的可视化。

Choosing meta-parameters. 一般来说,良好的无监督DA方法应提供方法来设置metaparameters(如λ、学习速率、动量率,方法)的网络体系结构以一种无监督的方式,即没有指带安全标签的数据时在目标域。在我们的方法中，我们可以通过观察测试误差对源域和域分类器误差的影响来评估整个系统的性能(以及改变超参数的影响)。一般来说，我们观察到自适应的成功与这些错误之间有很好的对应关系(当源域测试错误较低时，自适应更成功，而域分类器错误较高时)。此外，根据(Tzeng et al.， 2014)中提出的计算均值之间的差值，可以选取所连接的域适配器所在的层。

4.1. Results

现在我们讨论实验设置和结果。在每种情况下，我们对源数据集进行训练，并在不同的目标域数据集上进行测试，这些数据集在域之间具有相当大的迁移(参见图2)。

MNIST → MNIST-M. 我们的第一个实验处理MNIST数据集(LeCun et al.， 1998) (source)。为了获得目标域(MNIST-M)，我们将从BSDS500的彩色照片中随机抽取的原始集合上的数字混合到patch上(Arbelaez et al.， 2011)。这个操作被正式定义为两个图像 $I^{1}, I^{2}$ ，因为 $I_{i j k}^{o u t}=\left|I_{i j k}^{1}-I_{i j k}^{2}\right|$ ，其中I, j是一个像素的坐标，k是一个通道索引。换句话说，输出示例是通过从照片中提取一个补丁生成的，将其像素移动到与数字像素对应的位置。对于人类来说，与原始数据集相比，分类任务只会变得稍微困难一些(数字仍然可以清楚地区分)，而对于接受MNIST训练的CNN来说，这个领域是相当不同的，因为背景和笔画不再是恒定的。因此，仅使用源代码的模型性能很差。我们的方法成功地对齐了特征分布(图3)，这导致了成功的适应结果(考虑到适应是无监督的)。与此同时，o

Synthetic numbers → SVHN. 为了解决合成数据训练和真实数据测试的常见场景，我们使用街景房号数据集SVHN (Netzer et al.， 2011)作为目标域，合成数字作为源。后者(SYN数字)由我们自己通过改变文本(包括不同的一位数、二位数和三位数)、位置、方向、背景和笔画颜色以及模糊度，从Windows字体生成的50万张图像组成。人工选取变异度来模拟SVHN，但两个数据集的差异较大，最大的差异是SVHN图像背景中的结构化杂波。提出的基于反向传播的训练方法，较好地解决了仅使用源数据训练与使用已知目标标签的目标域数据训练之间三分之二的差距。相比之下，SA (Fernando et al.， 2013)并没有显著提高分类精度，这凸显了适应任务比MNIST实验更具挑战性。

MNIST ↔ SVHN. 在本实验中，我们进一步增大了分布之间的差距，并对MNIST和SVHN进行了测试，两者在外观上存在显著差异。在前150个时代，即使没有适应能力，SVHN的训练也面临着分类错误居高不下的挑战。为了避免最终得到一个很差的局部极小值，因此，这里不使用学习率退火。显然，这两个方向(MNIST SVHN和SVHN MNIST)并不相同困难。由于SVHN的多样性，在SVHN上训练的模型具有一定的推广意义更通用，在MNIST数据集上执行得更合理。事实证明确实如此，特性分布的出现支持这种情况。我们观察到，当我们将这些域输入到只接受MNIST训练的CNN时，它们之间有相当强的分离，而对于接受svhn训练的网络，这些特性则更加混杂。这一差异可能解释了为什么我们的方法在SVHN→MNIST场景中通过自适应成功地提高了性能(见表1)，但不是在相反的方向(SA不能在这个c中执行自适应)。

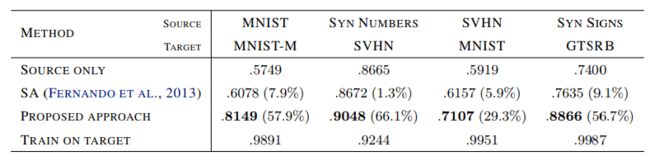DANN：Unsupervised Domain Adaptation by Backpropagation_第4张图片

表1。用于不同源和目标域的数字图像分类的分类精度。mist - m对应于非均匀背景下的差分混合数字。第一行对应较低的性能界限(即如果没有执行任何调整)。最后一行对应于使用已知类标签(DA性能的上限)对目标域数据进行训练。对于两种DA方法(我们的方法和(Fernando et al.， 2013))中的每一种，我们都展示了下界和上界之间的差距被覆盖了多少(在括号中)。在所有五种情况下，我们的方法都有显著的优势(Fernando et al.， 2013)，并覆盖了很大一部分差距。

Synthetic Signs → GTSRB. 总的来说，这个设置类似于SYN number SVHN实验，只是由于类的数量显著增加(43个而不是10个)，所以特性的分布更加复杂。对于源域，我们获得了100,000张模拟各种拍摄条件的合成图像(我们称之为SYN符号)。再次，我们的方法实现了性能的显著提高，再次证明了它适合于从合成到实际数据的适应。作为一个附加实验，我们也评估了半监督域自适应算法，即当一个额外提供了少量的标记目标数据。为此，我们将GTSRB分为火车集(带有标签的1280个随机样本)和验证集(数据集的其余部分)。验证部分仅用于评估，不参与适配。随着标签预测器现在暴露在目标数据中，训练过程略有变化。

图4显示了整个训练过程中验证错误的变化。虽然从图中可以清楚地看出，我们的方法可以应用于半监督设置中，但是对于半监督设置的验证还有待进一步的工作。

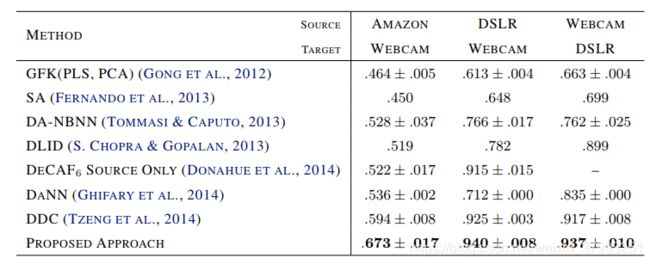
Office dataset. 最后，我们对OFFICE dataset上的方法进行了评估，该数据集由三个不同的域组成:AMAZON、DSLR和WEBCAM。与之前讨论过的数据集不同，OFFICE非常小，在最大域中只有2817张带标签的图像分布在31个不同类别中。可用数据的数量对于深度模型的成功训练至关重要，因此我们选择对在ImageNet上进行预训练的CNN进行微调(Jia et al.， 2014)，正如DA最近的一些工作(Donahue et al., 2014; Tzeng et al., 2014; Hoffman et al., 2013)。我们使用完全相同的网络架构，用域分类器替代基于域均值的正则化，从而使我们的方法更具有可比性(Tzeng et al.， 2014)。在之前的大部分工作中，我们使用5个随机分割来评估我们的方法，每个随机分割对应3个通常用于评估的传输任务。我们的训练方案接近(Tzeng et al., 2014; Saenko et al., 2010; Gong et al., 2012)，因为我们使用相同数量的标记源域图像每个类别。与那些作品不同，与DLID (S. Chopra & Gopalan, 2013)我们使用整个未标记目标域(我们方法的前提是目标域中未标记数据的丰富性)。在这种转换设置下，我们的方法能够极大地提高先前报道的最先进的无监督自适应精度(表2)，特别是在最具挑战性的AMAZON WEBCAM场景中(两个领域的领域迁移最大)。

DANN：Unsupervised Domain Adaptation by Backpropagation_第5张图片

表2。在标准OFFICE (Saenko et al.， 2010)数据集上对不同DA方法的准确性进行评估。我们的方法(最后一行)比竞争对手设置的最新技术更好。

5. Discussion

提出了一种新的基于深度前馈体系结构的无监督域自适应方法，该方法允许基于源域的大量带注释数据和目标域的大量无注释数据进行大规模训练。与以前的许多浅层和深层DA技术类似，通过调整这两个领域的特性分布来实现自适应。然而，与以前的方法不同，对齐是通过标准的反向传播训练完成的。因此，该方法具有相当的可伸缩性，可以使用任何深度学习包来实现。为此，我们计划发布梯度反转层的源代码，以及作为Caffe扩展的使用示例(Jia等，2014)。

对大规模任务和半监督环境的进一步评价构成今后的工作。同样有趣的是，该方法能否从特性提取器的良好初始化中获益。为此，一个自然的选择是使用 (Glorot et al., 2011; S. Chopra & Gopalan, 2013)，有效利用(Glorot et al., 2011; S. Chopra & Gopalan, 2013)，作为方法的初始化。

你可能感兴趣的:(transfer,learning,Transfer,Learning)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据 AIGC AGI LLM Java Python 架构设计 Agent 程序员实现财富自由
深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
初识HTTP（1） S1mple_easy 计算机网络学习笔记 http
HTTP基本概念HTTP是超⽂本传输协议，也就是HyperTextTransferProtocol超文本传输协议：HTTP是一个在计算机世界⾥专⻔在两点之间传输⽂字、图⽚、⾳频、视频等超⽂本数据的约定和规范。HTTP常见的状态码具体含义常见状态码1xx提示信息，表示目前是协议处理状态，还需后续操作2xx成功，报文已经收到并被正确处理200/204/2063xx重定向，资源位置发生变动，需要客户端重
云服务业界动态简报-20180128 Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
ResNet的半监督和半弱监督模型 Valar_Morghulis
Billion-scalesemi-supervisedlearningforimageclassificationhttps://arxiv.org/pdf/1905.00546.pdfhttps://github.com/facebookresearch/semi-supervised-ImageNet1K-models/权重在timm中也有：https://hub.fastgit.org/r
联邦学习 Federated learning Google I/O‘19 笔记努力搬砖的星期五笔记联邦学习机器学习机器学习 tensorflow
FederatedLearning:MachineLearningonDecentralizeddatahttps://www.youtube.com/watch?v=89BGjQYA0uE文章目录FederatedLearning:MachineLearningonDecentralizeddata1.DecentralizeddataEdgedevicesGboard:mobilekeyboa
PCL 怎样可视化深度图像 LeonDL168 PCL 计算机视觉人工智能视觉检测图像处理算法
本小节讲解如何可视化深度图像的两种方法，在3D视窗中以点云形式进行可视化（深度图像来源于点云），另一种是，将深度值映射为颜色，从而以彩色图像方式可视化深度图像。代码首先，在PCL（PointCloudLearning）中国协助发行的书提供光盘的第7章例2文件夹中，打开名为range_image_visualization.cpp的代码文件，同文件夹下可以找到相关的测试点云文件room_scan1.
【拖拽】自定义拖拽图标风露_
一、知识点设置被拖拽的元素draggable为true(HTML5新特性)关键方法：voiddataTransfer.setDragImage(img,xOffset,yOffset);注意点：Note:Ifthe[Element]isanexisting[HTMLElement],itneedstobevisibleintheviewportinordertobeshownasadragfeed
TCP实现FTP功能学不会のC tcp/ip linux c语言网络网络协议
文件传输协议（FileTransferProtocol，FTP）是一种在网络中进行文件传输的广泛使用的标准协议。作为网络通信中的基础工具，FTP允许用户通过客户端软件与服务器进行交互，实现文件的上传、下载和其他文件操作。FTP工作在OSI模型的应用层，通常使用TCP作为其传输协议，确保数据传输的可靠性和顺序性。项目要求有服务器和客户端代码，基于TCP写的。在同一路径下，将客户端可执行代码复制到其他
sftp上传和下载文件王小工 Linux linux
SFTP（SSHFileTransferProtocol）是一种基于SSH协议的文件传输协议，它提供了文件传输过程中的加密和验证功能，确保了数据的安全性。SFTP上传和下载文件的过程可以通过多种方式实现，包括使用SFTP客户端软件、命令行工具或编程SDK等。以下是SFTP上传和下载文件的基本步骤和方法：一、SFTP客户端软件操作软件选择与安装：FileZilla：一款广受欢迎的开源FTP客户端，支
http和https区别 m0_73882020 http
HTTP（超文本传输协议）和HTTPS（安全超文本传输协议）是用于在互联网上传输数据的协议。它们之间的主要区别在于安全性：HTTP（HypertextTransferProtocol）:加密:HTTP不对传输的数据进行加密，数据在传输过程中是以明文形式进行的。这意味着任何人都可以在网络中拦截并读取数据。端口:默认使用80端口。适用场景:适用于对安全要求不高的普通网页。HTTPS（Hypertext
Awesome TensorFlow weixin_30594001 人工智能移动开发大数据
AwesomeTensorFlowAcuratedlistofawesomeTensorFlowexperiments,libraries,andprojects.Inspiredbyawesome-machine-learning.WhatisTensorFlow?TensorFlowisanopensourcesoftwarelibraryfornumericalcomputationusin
【ShuQiHere】探索人工智能核心：机器学习的奥秘 ShuQiHere 人工智能机器学习
【ShuQiHere】什么是机器学习？机器学习（MachineLearning,ML）是人工智能（ArtificialIntelligence,AI）中最关键的组成部分之一。它使得计算机不仅能够处理数据，还能从数据中学习，从而做出预测和决策。无论是语音识别、自动驾驶还是推荐系统，背后都依赖于机器学习模型。机器学习与传统的编程不同，它不再依赖于人类编写的固定规则，而是通过数据自我改进模型，从而更灵活
综述论文“A Survey of Zero-Shot Learning: Settings, Methods, and Applications” 硅谷秋水机器学习机器学习神经网络深度学习
该零样本学习综述，发表于ACMTrans.Intell.Syst.Technol.10,2,Article13(January2019)摘要：大多数机器学习方法着重于对已经在训练中看到其类别的实例进行分类。实际上，许多应用程序需要对实例进行分类，而这些实例的类以前没有见过。零样本学习（Zero-ShotLearning）是一种强大而有前途的学习范例，其中训练实例涵盖的类别与想分类的类别是不相交的。
机器学习 VS 表示学习 VS 深度学习 Efred.D 人工智能机器学习深度学习人工智能
文章目录前言一、机器学习是什么?二、表示学习三、深度学习总结前言本文主要阐述机器学习,表示学习和深度学习的原理和区别.一、机器学习是什么?机器学习(machinelearning),是从有限的数据集中学习到一定的规律,再把学到的规律应用到一些相似的样本集中做预测.机器学习的历史可以追溯到20世纪40年代McCulloch提出的人工神经元网络,目前学界大致把机器学习分为传统机器学习和机器学习两个类别
端到端的自动驾驶论文与代码整理大别山伧父自动驾驶
LearningbyCheatinggithubcodearxivpaperconferenceonrobotlearning最新进展(May2021)Checkoutourlatestfollow-upwork:WorldonRails(2020)Checkoutoursubmissiontothe2020CARLAChallenge!pass
妙贼警探第1季第4集中英台词整理和单词统计 littleori
妙贼警探第1季第4集中英台词整理和单词统计英文中文Whatareyouthinking?你在想什么I'mthinkingitwastheaccountant.我想是那个会计Inthelawoffice.律师事务所里的那个Withtheillegalwiretransfer?非法电汇Eitherthat,orcolonelmustardinthelibrary.要么是他要么就是图书馆里的芥末上校[推
Lt-8 Multithreading yanlingyun0210 java
IntendedLearningOutcomesTounderstandtheconceptofconcurrency.Tounderstandthedifferenceofaprocessandathread.TodefineathreadusingtheThreadclassandRunnableinterface.TocontrolthreadswithvariousThreadmethod
如何使用Pytorch-Metric-Learning？鱼儿也有烦恼 PyTorch pytorch
文章目录如何使用Pytorch-Metric-Learning？1.Pytorch-Metric-Learning库9个模块的功能1.1Sampler模块1.2Miner模块1.3Loss模块1.4Reducer模块1.5Distance模块1.6Regularizer模块1.7Trainer模块1.8Tester模块1.9Utils模块2.如何使用PyTorchMetricLearning库中的
NIO笔记03-文件编程齐飞 nio 笔记后端 java
文章目录1FileChannel获取读取写入关闭位置大小强制写入2两个Channel传输数据3Path4Files检查文件是否存在创建一级目录创建多级目录用拷贝文件(和transferTo效率相仿)移动文件删除文件删除目录遍历目录文件拷贝多级目录1FileChannel⚠️FileChannel工作模式：FileChannel只能工作在阻塞模式下获取不能直接打开FileChannel，必须通过Fi
HTTPS和HTTP区别是什么？全真王重阳 #计算机网络 http https 网络协议网络 408 计算机网络
HTTP和HTTPS是两种协议，分别是HyperTextTransferProtocol和HyperTextTransferProtocolSecure。HTTPS还经常被称为HTTPoverSSL或者HTTPoverTSL，HTTPS经由HTTP进行通信，但利用SSL/TLS来加密数据包。他们的区别主要由以下几个方面：安全性:HTTP:HTTP是明文传输的，这意味着数据在传输过程中不加密，容易受
推荐开源项目：PyTorch-Metric-Learning 潘惟妍
推荐开源项目：PyTorch-Metric-Learningpytorch-metric-learningTheeasiestwaytousedeepmetriclearninginyourapplication.Modular,flexible,andextensible.WritteninPyTorch.项目地址:https://gitcode.com/gh_mirrors/py/pytorc
推荐：FastAPI驱动的稳定扩散LLMs演示项目褚知茉Jade
推荐：FastAPI驱动的稳定扩散LLMs演示项目FastAPI-for-Machine-Learning-Live-DemoThisrepositorycontainsthefilestobuildyourveryownAIimagegenerationwebapplication!OutlinedarethecorecomponentsoftheFastAPIwebframework,anda
【python】【Ray的概述】资源存储库 python 开发语言
Overview概述Rayisanopen-sourceunifiedframeworkforscalingAIandPythonapplicationslikemachinelearning.Itprovidesthecomputelayerforparallelprocessingsothatyoudon’tneedtobeadistributedsystemsexpert.Rayminimi
什么是监督学习（Supervised Learning）救救孩子把 AI AI 学习
一、监督学习概述监督学习（SupervisedLearning）是一种极具威力的机器学习方法，能够训练算法以识别数据中的模式，并据此进行精准的预测或分类。借助已有的标记数据，监督学习模型学会了从输入到输出的映射关系，进而在各类实际问题中实现自动化决策。无论是医疗诊断、金融市场分析、客户行为预测，还是提升生产效率以及个性化推荐系统等领域，监督学习都彰显出巨大的潜力与价值。随着技术的持续进步，监督学习
【已解决】如何打开ftp文件合集 moz与京 2024年报错/问题等整理服务器运维计算机网络
别人分享了一个文件夹，说需要的文件就在ftp://xx.xx.x.xxx:xxxx下面的文件目录中，一下子看蒙了。本来以为是常见的链接，但是发现开头是ftp协议。深感困惑，上网搜索以后才知道："FTP（FileTransferProtocol，文件传输协议）是一种用于在计算机网络上进行文件传输的标准协议。它主要用于在客户端和服务器之间传输文件。以下是一些关于FTP协议的关键知识点：1.基本概念：F
使用3DUNet训练自己的数据集（pytorch）— 医疗影像分割编程日记✧ 智能医疗 pytorch 人工智能 python 计算机视觉图像处理深度学习健康医疗
代码：lee-zq/3DUNet-Pytorch:3DUNetimplementedwithpytorch(github.com)文章<cicek16miccai.pdf(uni-freiburg.de)3DU-Net:LearningDenseVolumetricSegmentation
探索任务的隐秘世界：推荐Task2Vec 邓越浪Henry
探索任务的隐秘世界：推荐Task2Vecaws-cv-task2vecOfficialcodeforthepaper"Task2Vec:TaskEmbeddingforMeta-Learning"(https://arxiv.org/abs/1902.03545,ICCV2019)项目地址:https://gitcode.com/gh_mirrors/aw/aws-cv-task2vec在机器学习
论文阅读笔记: DINOv2: Learning Robust Visual Features without Supervision 小夏refresh 论文计算机视觉深度学习论文阅读笔记深度学习计算机视觉人工智能
DINOv2:LearningRobustVisualFeatureswithoutSupervision论文地址:https://arxiv.org/abs/2304.07193代码地址:https://github.com/facebookresearch/dinov2摘要大量数据上的预训练模型在NLP方面取得突破，为计算机视觉中的类似基础模型开辟了道路。这些模型可以通过生成通用视觉特征(即无
继之前的线程循环加到窗口中运行 3213213333332132 java thread JFrame JPanel
之前写了有关java线程的循环执行和结束，因为想制作成exe文件，想把执行的效果加到窗口上，所以就结合了JFrame和JPanel写了这个程序，这里直接贴出代码，在窗口上运行的效果下面有附图。 package thread; import java.awt.Graphics; import java.text.SimpleDateFormat; import java.util
linux 常用命令 BlueSkator linux 命令
1.grep 相信这个命令可以说是大家最常用的命令之一了。尤其是查询生产环境的日志，这个命令绝对是必不可少的。但之前总是习惯于使用（grep -n 关键字文件名）查出关键字以及该关键字所在的行数，然后再用（sed -n '100,200p' 文件名），去查出该关键字之后的日志内容。但其实还有更简便的办法，就是用（grep -B n、-A n、-C n 关键
php heredoc原文档和nowdoc语法 dcj3sjt126com PHP heredoc nowdoc
<!doctype html> <html lang="en"> <head> <meta charset="utf-8"> <title>Current To-Do List</title> </head> <body> <?
overflow的属性周华华 JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&q
《我所了解的Java》——总体目录 g21121 java
准备用一年左右时间写一个系列的文章《我所了解的Java》，目录及内容会不断完善及调整。在编写相关内容时难免出现笔误、代码无法执行、名词理解错误等，请大家及时指出，我会第一时间更正。 &n
[简单]docx4j常用方法小结 53873039oycg docx
本代码基于docx4j-3.2.0，在office word 2007上测试通过。代码如下: import java.io.File; import java.io.FileInputStream; import ja
Spring配置学习云端月影 spring配置
首先来看一个标准的Spring配置文件 applicationContext.xml <?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi=&q
Java新手入门的30个基本概念三 aijuans java 新手 java 入门
17.Java中的每一个类都是从Object类扩展而来的。　　18.object类中的equal和toString方法。　　equal用于测试一个对象是否同另一个对象相等。　　toString返回一个代表该对象的字符串,几乎每一个类都会重载该方法,以便返回当前状态的正确表示.(toString 方法是一个很重要的方法)　　 19.通用编程:任何类类型的所有值都可以同object类性的变量来代替。　
《2008 IBM Rational 软件开发高峰论坛会议》小记 antonyup_2006 软件测试敏捷开发项目管理 IBM 活动
我一直想写些总结,用于交流和备忘,然都没提笔,今以一篇参加活动的感受小记开个头,呵呵! 其实参加《2008 IBM Rational 软件开发高峰论坛会议》是9月4号,那天刚好调休.但接着项目颇为忙,所以今天在中秋佳节的假期里整理了下. 参加这次活动是一个朋友给的一个邀请书,才知道有这样的一个活动,虽然现在项目暂时没用到IBM的解决方案,但觉的参与这样一个活动可以拓宽下视野和相关知识.
PL/SQL的过程编程,异常,声明变量,PL/SQL块百合不是茶 PL/SQL的过程编程异常 PL/SQL块声明变量
PL/SQL; 过程; 符号; 变量; PL/SQL块; 输出; 异常; PL/SQL 是过程语言(Procedural Language)与结构化查询语言(SQL)结合而成的编程语言PL/SQL 是对 SQL 的扩展,sql的执行时每次都要写操作
Mockito(三)--完整功能介绍 bijian1013 持续集成 mockito 单元测试
mockito官网：http://code.google.com/p/mockito/，打开documentation可以看到官方最新的文档资料。一.使用mockito验证行为 //首先要import Mockito import static org.mockito.Mockito.*; //mo
精通Oracle10编程SQL(8)使用复合数据类型 bijian1013 oracle 数据库 plsql
/* *使用复合数据类型 */ --PL/SQL记录 --定义PL/SQL记录 --自定义PL/SQL记录 DECLARE TYPE emp_record_type IS RECORD( name emp.ename%TYPE, salary emp.sal%TYPE, dno emp.deptno%TYPE ); emp_
【Linux常用命令一】grep命令 bit1129 Linux常用命令
grep命令格式 grep [option] pattern [file-list] grep命令用于在指定的文件(一个或者多个,file-list)中查找包含模式串(pattern)的行,[option]用于控制grep命令的查找方式。 pattern可以是普通字符串，也可以是正则表达式，当查找的字符串包含正则表达式字符或者特
mybatis3入门学习笔记白糖_ sql ibatis qq jdbc 配置管理
MyBatis 的前身就是iBatis，是一个数据持久层(ORM)框架。 MyBatis 是支持普通 SQL 查询，存储过程和高级映射的优秀持久层框架。MyBatis对JDBC进行了一次很浅的封装。以前也学过iBatis，因为MyBatis是iBatis的升级版本，最初以为改动应该不大，实际结果是MyBatis对配置文件进行了一些大的改动，使整个框架更加方便人性化。
Linux 命令神器：lsof 入门 ronin47 lsof
lsof是系统管理/安全的尤伯工具。我大多数时候用它来从系统获得与网络连接相关的信息，但那只是这个强大而又鲜为人知的应用的第一步。将这个工具称之为lsof真实名副其实，因为它是指“列出打开文件（lists openfiles）”。而有一点要切记，在Unix中一切（包括网络套接口）都是文件。有趣的是，lsof也是有着最多
java实现两个大数相加，可能存在溢出。 bylijinnan java实现
import java.math.BigInteger; import java.util.regex.Matcher; import java.util.regex.Pattern; public class BigIntegerAddition { /** * 题目：java实现两个大数相加，可能存在溢出。 * 如123456789 + 987654321
Kettle学习资料分享，附大神用Kettle的一套流程完成对整个数据库迁移方法 Kai_Ge Kettle
Kettle学习资料分享 Kettle 3.2 使用说明书目录概述..........................................................................................................................................7 1.Kettle 资源库管
[货币与金融]钢之炼金术士 comsci 金融
自古以来,都有一些人在从事炼金术的工作.........但是很少有成功的那么随着人类在理论物理和工程物理上面取得的一些突破性进展...... 炼金术这个古老
Toast原来也可以多样化 dai_lm android toast
Style 1：默认 Toast def = Toast.makeText(this, "default", Toast.LENGTH_SHORT); def.show(); Style 2：顶部显示 Toast top = Toast.makeText(this, "top", Toast.LENGTH_SHORT); t
java数据计算的几种解决方法3 datamachine java hadoop ibatis r-langue r
4、iBatis 简单敏捷因此强大的数据计算层。和Hibernate不同，它鼓励写SQL，所以学习成本最低。同时它用最小的代价实现了计算脚本和JAVA代码的解耦，只用20%的代价就实现了hibernate 80%的功能,没实现的20%是计算脚本和数据库的解耦。复杂计算环境是它的弱项，比如：分布式计算、复杂计算、非数据
向网页中插入透明Flash的方法和技巧 dcj3sjt126com html Web Flash
将 Flash 作品插入网页的时候，我们有时候会需要将它设为透明，有时候我们需要在Flash的背面插入一些漂亮的图片，搭配出漂亮的效果……下面我们介绍一些将Flash插入网页中的一些透明的设置技巧。　　一、Swf透明、无坐标控制　　首先教大家最简单的插入Flash的代码，透明，无坐标控制：　　注意wmode="transparent"是控制Flash是否透明
ios UICollectionView的使用 dcj3sjt126com
UICollectionView的使用有两种方法，一种是继承UICollectionViewController，这个Controller会自带一个UICollectionView；另外一种是作为一个视图放在普通的UIViewController里面。个人更喜欢第二种。下面采用第二种方式简单介绍一下UICollectionView的使用。 1.UIViewController实现委托，代码如
Eos平台java公共逻辑蕃薯耀 Eos平台java公共逻辑 Eos平台 java公共逻辑
Eos平台java公共逻辑 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年6月1日 17:20:4
SpringMVC4零配置--Web上下文配置【MvcConfig】 hanqunfeng springmvc4
与SpringSecurity的配置类似，spring同样为我们提供了一个实现类WebMvcConfigurationSupport和一个注解@EnableWebMvc以帮助我们减少bean的声明。 applicationContext-MvcConfig.xml  <
解决ie和其他浏览器poi下载excel文件名乱码 jackyrong Excel
使用poi,做传统的excel导出，然后想在浏览器中，让用户选择另存为，保存用户下载的xls文件，这个时候，可能的是在ie下出现乱码（ie,9,10,11),但在firefox,chrome下没乱码，因此必须综合判断，编写一个工具类： /** * * @Title: pro
挥洒泪水的青春 lampcy 编程生活程序员
2015年2月28日，我辞职了，离开了相处一年的触控，转过身--挥洒掉泪水，毅然来到了兄弟连，背负着许多的不解、质疑——”你一个零基础、脑子又不聪明的人，还敢跨行业，选择Unity3D？“，”真是不自量力••••••“，”真是初生牛犊不怕虎•••••“，••••••我只是淡淡一笑，拎着行李----坐上了通向挥洒泪水的青春之地——兄弟连！这就是我青春的分割线，不后悔，只会去用泪水浇灌——已经来到
稳增长之中国股市两点意见-----严控做空，建立涨跌停版停牌重组机制 nannan408
对于股市，我们国家的监管还是有点拼的，但始终拼不过飞流直下的恐慌，为什么呢？笔者首先支持股市的监管。对于股市越管越荡的现象，笔者认为首先是做空力量超过了股市自身的升力，并且对于跌停停牌重组的快速反应还没建立好，上市公司对于股价下跌没有很好的利好支撑。我们来看美国和香港是怎么应对股灾的。美国是靠禁止重要股票做空，在
动态设置iframe高度(iframe高度自适应) Rainbow702 JavaScript iframe contentDocument 高度自适应局部刷新
如果需要对画面中的部分区域作局部刷新，大家可能都会想到使用ajax。但有些情况下，须使用在页面中嵌入一个iframe来作局部刷新。对于使用iframe的情况，发现有一个问题，就是iframe中的页面的高度可能会很高，但是外面页面并不会被iframe内部页面给撑开，如下面的结构： <div id="content"> <div id=&quo
用Rapael做图表 tntxia rap
function drawReport(paper,attr,data){ var width = attr.width; var height = attr.height; var max = 0; &nbs
HTML5 bootstrap2网页兼容（支持IE10以下） xiaoluode html5 bootstrap
<!DOCTYPE html> <html> <head lang="zh-CN"> <meta charset="UTF-8"> <meta http-equiv="X-UA-Compatible" content="IE=edge">