《算法》读书笔记（二）

第1章 基础

---

本书研究的是算法和数据结构，本章介绍的是学习算法和数据结构所需要的基本工具。它讲解了在随后的章节中用来实现、分析和比较算法的基本原则和方法，包括Java编程模型、数据抽象、基本数据结构、集合类的抽象数据类型、算法性能分析的方法和一个案例分析。

PS：算法式思考（algorithmic thinking），这词挺有趣的

1.1 基础编程模型

介绍了相关的语法、语言特性和库。
本书使用Java来实现算法。我们把描述和实现算法所用到的语言特性、软件库和操作系统特性总称为基础编程模型。另一本入门书籍An Introduction to Programming in Java: An Interdisciplinary Approach也使用了这个模型。

1.1.1 Java程序的基本结构

一段Java程序（类）要么是一个静态方法（函数）库，要么定义了一个数据结构。要创建静态方法库和定义数据类型，会用到如下几种语法：原始数据类型、语句（声明、赋值、条件、循环、调用和返回）、数组、静态方法、字符串、标准输入/输出、数据抽象。

1.1.2 原始数据类型与表达式

int、double、boolean、char、long、short、byte、float。

1.1.3 语句

声明、赋值、条件、循环（break和continue）、调用和返回语句。

1.1.4 简便记法

声明并初始化、隐式赋值、单语句代码段、for语句。

1.1.5 数组

创建、初始化、二维数组。
注意：数组名表示的是整个数组——如果我们将一个数组变量赋予另一个变量，那么两个变量将会指向同一个数组。在方法中使用的参数变量能够引用调用者的数组并改变其内容。Talk is cheap. Show me the code.

public class C1_1_6_Arrays {
    public static void main(String[] args) {
        int[] a = { 0, 1, 2, 3, 4 };
        change(a);
        System.out.println(a[0]);
    }

    private static void change(int[] a) {
        a[0] = 5;
    }
}

打印结果是5。

1.1.6 静态方法

static、递归。
// 此处介绍了二分查找的递归实现，只看代码的话理解起来还是不太容易的，此处存疑。

1.1.7 API

自定义标准库。
其中讲到了两个方法的源码，discrete()（返回i的概率为a[i]），和shuffle()（将数组a随机排序）。也把代码在这贴出来。

public class C1_1_7_StdRandom {
    // 出现i的概率为a[i]
    public static int discrete(double[] a) {
        // a[]中各元素之和必须等于1
        double r = StdRandom.random();
        double sum = 0.0;
        for (int i = 0; i < a.length; i++) {
            sum += a[i];
            if (sum >= r) {
                return i;
            }
        }
        return -1;
    }

    // 随机将 double 数组中的元素排序
    public static void shuffle(double[] a) {
        for (int i = 0; i < a.length; i++) {
            // 将 a[i] 和 a[i...N-1] 中任意一个元素交换
            int r = i + StdRandom.uniform(a.length - i);
            double temp = a[r];
            a[r] = a[i];
            a[i] = temp;
        }
    }
}

你应该将自己编写的每一个程序都当做一个日后可以重用的库。也可以想成你现在写的代码两年后甚至数十年后还会有人在维护，要对自己的代码负责。

1.1.8 字符串

String。

1.1.9 输入输出

标准输入输出、格式化输出、标准绘图库。
对于格式化输出还是很有趣的，我把相应的测试代码写在了“C1_1_9_PrintfTest”中。

1.1.10 二分查找

以二分查找作为例子简单回顾。

1.1.11 展望

1.2 数据抽象

介绍了用Java实现抽象数据类型的过程，包括定义它的应用编程接口（API）然后通过Java的类机制来实现它以供各种用例使用——自定义类。

1.2.1 使用抽象数据类型

为了编写一个使用Counter（计数器）的简单数据类型的程序，需要写一份API，并重写toString()方法。导包，创建对象，使用对象，将对象返回。
对象的数组。

1.2.2 抽象数据类型举例

介绍了很多Java内置的抽象数据类型：画图的、信息处理的、字符串、输入输出。

1.2.3 抽象数据类型的实现

介绍了类的相关知识，如构造函数、实例方法等。

1.2.4 更多抽象数据类型的实现

举例解释上一节：日期、累加器、可视化累加器。

1.2.5 数据类型的设计

封装、算法与抽象数据类型、接口、继承、字符串特点、等价性、内存管理、不可变形、异常、断言。

1.3 背包、队列和栈

用数组、变长数组和链表实现了背包、队列和栈的API，它们是全书算法实现的起点和样板。

1.3.1 API

无论做什么，先写API。每份API都含有一个无参数的构造函数、一个向集合中添加单个元素的方法、一个测试集合是否为空的方法和一个返回集合大小的方法。队列和栈都含有一个能够删除特定元素的方法。
泛型：我们定义一个集合，但不知道集合中储存数据的具体类型是什么，用 < T>表示。
自动装箱：int —> Integer
可迭代的集合类型：就是可以访问集合中的每一个元素的意思。
背包：一种元素之间没有相对顺序的集合，可以理解成一个背包中的弹球，每次迭代都是没有顺序的。我认为正是因为没有顺序，所以没有明确的办法区分出某一个元素，因此背包才不支持删除元素。
先进先出队列：好像没啥说的，就是队列呗。
下压栈：压栈弹栈，先进后出，基础概念。
算术表达式求值：用两个栈（一个用于保存运算符，一个用于保存操作数）实现表达式的运算。在不同的地方看过两次，真正用代码实现过一次，现在看来还跟陌生的东西一样。跟程序的机器级表示有神似之处。

1.3.2 集合类数据类型的实现

定容栈：作为热身，先来看一种表示容量固定的字符串栈的抽象数据类型，它只处理String值，要求用例指定容量且不支持迭代。在其构造函数中指定指定容量，用push()添加一个字符串，用pop()弹出一个字符串，用N的大小记录字符串数量，用N是否等于0判断栈是否为空。

public class FixedCapacityStackOfStrings {
    private String[] a; // stack entries
    private int N; // size

    public FixedCapacityStackOfStrings(int cap) {
        a = new String[cap];
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public int size() {
        return N;
    }

    public void push(String item) {
        a[N++] = item;
    }

    public String pop() {
        return a[--N];
    }
}

泛型：使用Item代替String，理论上就可以处理认识类型的数据了。
调整数组的大小：因为选择了用数组表示栈的容量，如果需要调整栈的大小，就需要调整数组的大小。说白了就是创建一个大小符合要求的新数组，然后把老数组的内容复制到新数组中，具体的代码比较简单就不贴了。
对象游离：说白了就是内存泄漏。
迭代：集合类数据类型的基本操作之一就是，能够使用Java的foreach语句通过迭代遍历并处理集合中的每个元素。我们决定使用Java的接口机制来实现迭代，即在类的声明中加入implements Iterable< Item>。当然，具体的方法实现在不同的需求中需要做不同的改动。

public interface Iterator {
boolean hasNext();
Item next();
void remove();
}

1.3.3 链表

结点记录：我们先用一个嵌套类来定义结点的抽象数据类型：

private class Node {
Item item;
Node next;
}

构造链表：要构造一条含有元素to、be和or的链表，我们首先为每个元素创造一个结点：

Node first = new Node();
Node second = new Node();
Node third = new Node();

并将每个结点的item域设为所需的值：

first.item = "to";
second.item = "be";
third.item = "or";

然后设置next域来构造链表：

first.next = second;
second.next = third;

链表表示的是一列元素，可以用以下数组表示同一列字符串：

String[] s = { "to", "be", "or" };

在表头插入结点：先创建一个结点oldfirst，把first保存在oldfirst中，再将一个新的结点赋给first，把它的item设为自己需要的内容，next指向oldfirst。

从表头删除结点：只需将first指向first.next。

在表尾插入节点：虽然操作简单，但不能草率的决定维护一个链接，如果不仔细斟酌，可能会出现问题。

其他位置的插入和删除操作：最好的解决方法是使用双向链表，没详讲。
遍历：

for (Node x = first; x != null; x = x.next)
{
// Process x.item.
}

栈的实现：先进后出，将栈保存为一条链表，栈的顶部即为表头，实例变量first指向栈顶，当使用push()压入一个元素时，即把一个元素添加到表头；当使用pop()删除一个元素时，即将该元素从表头删除。

public class Stack implements Iterable {
    private Node first; // 栈顶（最近添加的元素）
    private int N; // 元素数量

    private class Node { // 定义了结点的嵌套类
        Item item;
        Node next;
    }

    public boolean isEmpty() {
        return first == null;
    } // 或：N == 0

    public int size() {
        return N;
    }

    public void push(Item item) { // 向栈顶添加元素
        Node oldfirst = first;
        first = new Node();
        first.item = item;
        first.next = oldfirst;
        N++;
    }

    public Item pop() { // 从栈顶删除元素
        Item item = first.item;
        first = first.next;
        N--;
        return item;
    }
}

队列的实现：先进先出，将队列表示为一条从最早插入的元素到最近插入的元素的链表，实例变量first指向队列的开头，实例变量last指向队列的结尾。这样，要将一个元素入列，就把它添加到表尾；要将一个元素出列，就删除表头的结点。

public class Queue implements Iterable {
    private Node first; // 指向最早添加的结点的链接
    private Node last; // 指向最近添加的结点的链接
    private int N; // 队列中的元素数量

    private class Node { // 定义了结点的嵌套类
        Item item;
        Node next;
    }

    public boolean isEmpty() {
        return first == null; // 或：N == 0
    } 

    public int size() {
        return N;
    }

    public void enqueue(Item item) { // 向表尾添加元素
        Node oldlast = last;
        last = new Node();
        last.item = item;
        last.next = null;
        if (isEmpty())
            first = last;
        else
            oldlast.next = last;
        N++;
    }

    public Item dequeue() { // 从表头删除元素
        Item item = first.item;
        first = first.next;
        if (isEmpty())
            last = null;
        N--;
        return item;
    }
}

背包的实现：先进先出，不过不重要，要实现只需将栈中的push()改名为add()就行了，去掉多余的pop()。

public class Bag<Item> implements Iterable<Item> {
    private Node first; // 链表的首结点

    private class Node {
        Item item;
        Node next;
    }

    public void add(Item item) { // 和Stack的push()方法完全相同
        Node oldfirst = first;
        first = new Node();
        first.item = item;
        first.next = oldfirst;
    }

    public Iterator iterator() {
        return new ListIterator();
    }
    private class ListIterator implements Iterator<Item> {
        private Node current = first;
        public boolean hasNext() {
            return current != null;
        }
        public void remove() {
        }
        public Item next() {
            Item item = current.item;
            current = current.next;
            return item;
        }
    } // 为什么只有背包具体实现了迭代，之前的章节说在1.4里实现啊，存疑
}

1.3.4 综述

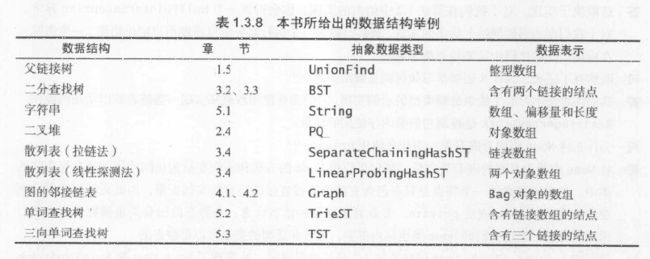
我们在本节中研究背包、队列和栈时描述数据结构和算法的方式是全书的原型（本书中的数据结构如图）。在研究一个新的应用领域时，我们将会按照以下步骤识别目标并使用数据抽象解决问题：

• 定义API；
• 根据特定的应用场景开发用例代码；
• 描述一种数据结构（一组值的表示），并在API所对应的抽象数据类型的实现中根据它定义类的实例变量；
• 描述算法（实现一组操作的方式），并根据它实现类中的实例方法；
• 分析算法的性能特点。
  

1.4 算法分析

性能是算法研究的一个核心问题。本节描述了分析算法性能的方法。

1.4.1 科学方法

可重现，可证伪。

1.4.2 观察

问题规模。
举例：以一个例子来说明预测程序运行时间的重要性。
计时器：创建一种表示计时器的抽象数据类型。
实验数据的分析：程序在不同的计算机上的运行时间之比通常是一个常数， T(N)=aN3 。

1.4.3 数学模型

近似：我们用-f(N)表示所有随着N的增大除以f(N)的结果趋近于1的函数。我们用g(N)~f(N)表示g(N)/f(N)随着N的增大趋近于1。
对增长数量级的猜想：ThreeSum（在N个数中找出三个和为0的整数元组的数量）的运行时间的增长数量级为 N3 。
成本模型：我们使用成本模型评估算法的性质，这个模型定义了我们所研究的算法中的基本操作。
总结：对于大多数程序，得到其运行时间的数学模型所需的步骤如下：

• 确定输入模型，定义问题的规模；
• 识别内循环；
• 根据内循环中的操作确定成本模型；
• 对于给定的输入，判断这些操作的执行频率。

1.4.4 增长数量级的分类

常数级别、对数级别、线性级别、线性对数级别、平方级别、立方级别、指数级别。

1.4.5 设计更快的算法

热身运动 2-sum：改进后的算法的思想是当且仅当-a[i]存在于数组中（且a[i]非零）时，然后对于数组中的每个a[i]，使用BinarySearch的rank()方法对-a[i]进行二分查找。
3-sum 问题的快速算法：和刚才一样，我们假设所有整数均各不相同。当且仅当-(a[i] + a[j]) 在数组中（不是a[i]也不是a[j]）时，整数对（a[i]和a[j]）为某个和为0的三元组的一部分。因此总运行时间和 N2logN 成正比。
下界：

• 实现并分析该问题的一种简单的算法。我们通常将它们成为暴力算法，例如ThreeSum和TwoSum。
• 考查算法的各种改进，它们通常都能降低算法所需的运行时间的增长数量级，例如 TwoSumFast 和 ThreeSumFast。
• 用实验证明新的算法更快。

1.4.6 倍率实验

下面这种方法可以简单有效地预测任意程序的性能并判断它们的运行时间大致的增长数量级。

• 开发一个输入生成器来产生实际情况下的各种可能的输入。
• 运行 DoublingRatio 程序，能够计算每次实验和上一次的运行时间的比值。
• 反复运行直到该比值趋近于极限 2b 。
• 它们的运行时间的增长数量级约为 Nb 。
• 要预测一个程序的运行时间，将上次观察得到的运行时间乘以 2b 并将N加倍，如此反复。

1.4.7 注意事项

大常数、非决定性的内循环、指令时间、系统因素、不分伯仲、对输入的强烈依赖、多个问题参量。

1.4.8 处理对于输入的依赖

对于许多问题，刚才所提到的注意事项中最突出的一个就是对于输入的依赖，因为在这种情况下程序的运行时间的变化范围可能非常大。因此如果我们想要预测它的性能，就需要对它进行更加细致的分析。
输入模型：一种方法是更加小心地对我们所要解决的问题所处理的输入模型。
对最坏情况下的性能的保证：在计算机系统中最坏情况是非常现实的忧虑，因此我们许多算法的设计已经考虑了为性能提供保证。
随机化算法、操作序列、均摊分析。

1.4.9 内存

1.4.10 展望

1.5 案例研究：union-find算法

用一个连通性问题作为例子结束本章。

1.5.1 动态连通性

问题的输入是一列整数对，其中每个整数都表示一个某种类型的对象，一对整数 p q 可以被理解为“p 和 q 是相连的”。如果已知的所有整数对都不能说明 p 和 q 是相连的，那么则将这一对整数写入到输出中。如果已知的数据可以说明 p 和 q 是相连的，那么程序应该忽略 p q 这对整数并继续处理输入中的下一对整数。

public class UF {
    private int[] id; // 分量id（以触点作为索引）
    private int count; // 分量数量

    public UF(int N) { // 初始化分量id数组
        count = N;
        id = new int[N];
        for (int i = 0; i < N; i++)
            id[i] = i;
    }

    public int count() {
        return count;
    }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    public int find(int p)

    public void union(int p, int q) 
    // 请见1.5.2.1节用例（quick-find）、1.5.2.3节用例（quick-union）和算法1.5（加权quick-union）
    public static void main(String[] args) { // 解决由StdIn得到的动态连通性问题
        int N = StdIn.readInt(); // 读取触点数量
        UF uf = new UF(N); // 初始化N个分量
        while (!StdIn.isEmpty()) {
            int p = StdIn.readInt();
            int q = StdIn.readInt(); // 读取整数对
            if (uf.connected(p, q))
                continue; // 如果已经连通则忽略
            uf.union(p, q); // 归并分量
            StdOut.println(p + " " + q); // 打印连接
        }
        StdOut.println(uf.count() + " components");
    }
}

1.5.2 实现

1.5.3

第2章 排序

---

深入研究各种排序算法，包括插入排序、选择排序、希尔排序、快速排序、归并排序和堆排序。同时我们还会讨论另外一些算法，它们用于解决几个与排序相关的问题，例如优先队列、选举以及归并。其中许多算法会成为后续章节中其他算法的基础。

2.1 初级排序算法

2.2 归并排序

2.3 快速排序

2.4 优先队列

2.5 应用

第3章 查找

---

讨论基本的和高级的查找算法，包括二叉查找树，平衡查找树和散列表。我们会梳理这些方法之间的关系并比较它们的性能。

3.1 符号表

3.2 二叉树查找

3.3 平衡树查找

3.4 散列表

3.5 应用

第4章 图

---

图的主要内容是对象和它们的连接，连接可能有权重和方向。利用图可以为大量重要而困难的问题建模，因此图算法的设计也是本书的一个主要研究领域。我们会研究深度优先搜索、广度优先搜索、连通性问题以及若干其他算法和应用，包括 Kruskal 和 Prim 的最小生成树算法、Dijkstra 和 Bellman-Ford 的最短路径算法。

4.1 无向图

4.2 有向图

4.3 最小生成树

4.4 最短路径

第5章 字符串

---

研究一系列处理字符串的算法，首先是对字符串键的排序和查找的快速算法，然后是子字符串查找、正则表达式模式匹配和数据压缩算法。此外，在分析一些本身就十分重要的基础问题之后，这一章对相关领域的前沿话题也作了介绍。

5.1 字符串排序

5.2 单词查找树

5.3 子字符串查找

5.4 正则表达式

5.5 数据压缩

第6章

---

这一章将讨论与本书内容有关的若干其他前沿研究领域，包括科学计算、运筹学和计算理论。我们会介绍性地讲一下基于事件的模拟、B树、后缀数组、最大流量问题以及其他高级主题，以帮助读者理解算法在许多有趣的前沿研究领域中所起到的巨大作用。最后，我们会讲一讲搜索问题、问题转化和NP完全性等算法研究的支柱理论，以及它们和本书内容的联系。