matlab入门---数值计算
matlab入门—数值计算
matlab的所有运算都是基于矩阵进行的,matlab中大多数数据几乎都是矩阵。在下面的介绍中主要从这几个方面介绍matlab基本的数值计算指令:
1.矩阵的创建
2.矩阵的运算
3.多项式的运算
4.线性插值
1.矩阵的创建
matlab中矩阵的创建主要有两种方式:
1.通过直接输入矩阵数据创建
2.通过调用矩阵创建函数创建
1.通过直接输入矩阵数据创建:
这是创建matlab矩阵最为常见的方式,直接输入的数据必须包括在[ ]中,数据间用空格或者逗号分隔,不同行的数据必须用分号分隔,矩阵中的每个元素可以是表达式,实数,复数等如:
(1)输入1×5的行矩阵,并赋给a:
用空格作为每行不同列数据之间的分隔符:
>> a=[1 2 3 4 5]
a =
1 2 3 4 5用“,”作为每行不同列数据之间的分隔符:
>> a=[1,2,3,4,5]
a =
1 2 3 4 5(2)创建2×3的行矩阵,并赋给a:
>> a=[2,3,4;1,5,7]
a =
2 3 4
1 5 7>> b=[1,6+7i,5;2,7.5,8]
b =
1.0000 6.0000 + 7.0000i 5.0000
2.0000 7.5000 8.0000 2.通过调用矩阵函数创建:
常用的矩阵创建函数如下:
rand(m,n)——————创建m行n列的随机矩阵
eye(m,n)——————-创建m行n列的单位矩阵
ones(m,n)—————–创建m行n列的全1矩阵
zeros(m,n)—————–创建m行n列的全零矩阵
另外还有稀疏矩阵、对角矩阵、魔方矩阵函数等,不一一举例。
>> rand(3,4)
ans =
0.8147 0.9134 0.2785 0.9649
0.9058 0.6324 0.5469 0.1576
0.1270 0.0975 0.9575 0.9706>> eye(3,3)
ans =
1 0 0
0 1 0
0 0 1>> ones(2,3)
ans =
1 1 1
1 1 1>> zeros(3,2)
ans =
0 0
0 0
0 03.矩阵的元素的修改
矩阵的元素可以通过索引的方式来修改,比如创建了一个3×3的随机矩阵a,现在想修改矩阵中第三行第3列的元素,将之修改为8,则可以通过a(3,3)=8来修改(注意,matlab的行列下标都是从0开始的,这一点不同于其他高级语言),具体过程如下:
>> a=rand(3,3)
a =
0.9572 0.1419 0.7922
0.4854 0.4218 0.9595
0.8003 0.9157 0.6557
>> a(3,3)=8
a =
0.9572 0.1419 0.7922
0.4854 0.4218 0.9595
0.8003 0.9157 8.0000
2.矩阵的运算
矩阵的运算类型比较多,常见的有:
矩阵的+、-、×、乘方、转置、左右上下翻转、求逆矩阵、求对角矩阵、矩阵开方、求矩阵的特征值和对角矩阵等,还有矩阵的数组运算等等。下面从一一介绍:
1.矩阵的+、-、×、乘方运算
(1)+、-运算
矩阵的+、-运算,要求参与运算的矩阵A与B必须有相同的行数和列数,在进行运算时,A与B两个矩阵对应位置上的元素各自相加得到最终结果,如果是单独的一个标量c与矩阵相加,则结果为该矩阵各个位置上的数各自加上该标量后的一个矩阵,具体如下。
两个矩阵A和B相加:
>> A=rand(2,2)
A =
0.0357 0.9340
0.8491 0.6787
>> B=ones(2,2)
B =
1 1
1 1
>> A+B
ans =
1.0357 1.9340
1.8491 1.6787矩阵A和一个标量5相加:
>> A
A =
0.0357 0.9340
0.8491 0.6787
>> A+5
ans =
5.0357 5.9340
5.8491 5.6787(2)矩阵×运算
矩阵A与B相乘时,A矩阵的列数必须等于B矩阵的行数才能相乘。其数学过程与意义不赘述。
>> A
A =
0.0357 0.9340
0.8491 0.6787
>> B
B =
1 1
1 1
>> A*B
ans =
0.9697 0.9697
1.5279 1.5279(3)矩阵乘方运算
矩阵的乘方运算,可以用A^b来表示,如果A表示矩阵,b表示一个标量,则表示b个矩阵进行矩阵乘法,如果A和b都表示矩阵,则运算无意义。
>> A
A =
0.0357 0.9340
0.8491 0.6787
>> b=2
b =
2
>> A^b
ans =
0.7944 0.6673
0.6067 1.25382.矩阵的数组运算
矩阵的数组的运算,用带“.”的运算符来进行运算,比如”.*”、”./”、”.^”等。矩阵的数组运算要求进行运算的矩阵数组A与B必须具备同样的维数大小,否则不能进行运算。
其运算结果为数组A与B的对应位置的数进行相应的*、/、^等运算,结果返回一个与A、B同等大小的数组。
A=rand(2,3)
A =
0.7547 0.6797 0.1626
0.2760 0.6551 0.1190
>> B=rand(2,3)
B =
0.4984 0.3404 0.2238
0.9597 0.5853 0.7513
>> A.*B
ans =
0.3761 0.2314 0.0364
0.2649 0.3834 0.0894
>> A./B
ans =
1.5143 1.9969 0.7266
0.2876 1.1193 0.1584
>> c=[1 2 0;1 1 1]
c =
1 2 0
1 1 1
>> A.^c
ans =
0.7547 0.4620 1.0000
0.2760 0.6551 0.1190
3.矩阵的其他运算
matlab中的矩阵运算除了以上的常用运算以外,还有不少的运算,这些运算大多是通过特定函数来实现的。
inv()——————求矩阵的逆矩阵
eig()—————-求矩阵的特征矩阵
det()——————求矩阵的行列式值
sqrt()—————–求矩阵的开方
diag()—————–求对角矩阵
‘———————求矩阵的转置
rot90()—————-将矩阵翻转90度
fliplr()—————–左右翻转
flipud()—————-上下翻转
tril()——————–抽取主下三角形
triu()——————–抽取主上三角形
reshape()—————实现矩阵的变维
>> a=magic(3)
a =
8 1 6
3 5 7
4 9 2
>> inv(a)
ans =
0.1472 -0.1444 0.0639
-0.0611 0.0222 0.1056
-0.0194 0.1889 -0.1028
>> det(a)
ans =
-360
>> diag(a)
ans =
8
5
2
>> sqrt(a)
ans =
2.8284 1.0000 2.4495
1.7321 2.2361 2.6458
2.0000 3.0000 1.4142
>> eig(a)
ans =
15.0000
4.8990
-4.8990
>> a'
ans =
8 3 4
1 5 9
6 7 2
>> a
a =
8 1 6
3 5 7
4 9 2
>> rot90(a)
ans =
6 7 2
1 5 9
8 3 4
>> fliplr(a)
ans =
6 1 8
7 5 3
2 9 4
>> flipud(a)
ans =
4 9 2
3 5 7
8 1 6
>> tril(a)
ans =
8 0 0
3 5 0
4 9 2
>> triu(a)
ans =
8 1 6
0 5 7
0 0 2
>> reshape(a,9,1)
ans =
8
3
4
1
5
9
6
7
2
3.多项式的运算
matlab中将多项式用其系数组成的向量来表示,从左到右依次表示多项式高阶系数到低阶系数。比如,4x^3+5x^2+6x+5可以表示为p=[4 5 6 5]。为了能够将这种向量化的多项式表示形象的表示成我们熟悉的多项式形式,如4x^3+5x^2+6x+5这种形式,可以用poly2str(p,’x’)将相应的向量表示成人们熟悉的数学表达形式。其中P代表多项式的向量,’x’表示我们要采用的未知数。当要对一个多项式表达式求根时,可以用roots(p)来对多项式求根,返回其求根结果。可以用poly(roots)从roots()函数求得的根中还原到原函数。matlab中还提供了polyder(p)函数求多项式的导数。
>> p=[4 5 6 5]
p =
4 5 6 5
>> poly2str(p,'x')
ans =
4 x^3 + 5 x^2 + 6 x + 5
>> roots(p)
ans =
-1.0000
-0.1250 + 1.1110i
-0.1250 - 1.1110i
>> poly(roots(p))
ans =
1.0000 1.2500 1.5000 1.2500
>> s=polyder(p)
s =
12 10 6
>> poly2str(p,'x')
ans =
4 x^3 + 5 x^2 + 6 x + 5
>> poly2str(s,'x')
ans =
12 x^2 + 10 x + 6
4.线性插值
在实际应用中,常常需要根据一些离散的数据点来估计出这些离散点之间的关联,以便用这种规律去预测后面的数据,这种运算称之为拟合,matlab中提供了polyfit(x,y,count)来进行,x,y表示要进行拟合的x与y坐标数据,count表示用最高次数为几次的多项式来拟合数据。polyval(p,x)提供了拟合后的函数进行计算的函数。拟合操作很方便,但是有时候在两个间隔的点之间,如果想要得到两点之间符合其他段多项式运算规律的数据的话,就要进行插值运算,在间断的两点之间模拟出相应的函数关系,据此推断出间断点之间的数据。matlab中包括interp1、interp2、spline三种插值操作,前两种分别表示一、二次插值,最后一种表示3次样条插值。
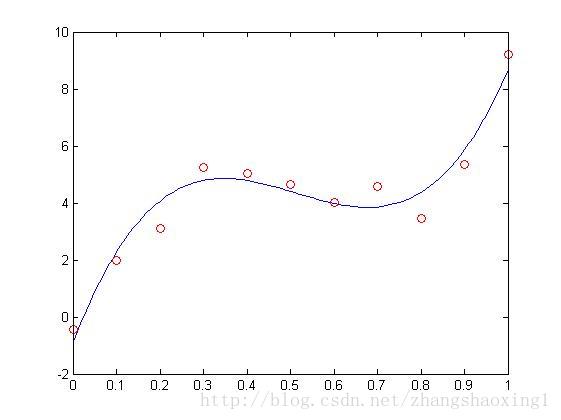
利用已知数据进行拟合:
>> x0=0:0.1:1;
>> y0=[-.447 1.978 3.11 5.25 5.02 4.66 4.01 4.58 3.45 5.35 9.22];
>> p=polyfit(x0,y0,3);
>> x=0:0.01:1;
>> y=polyval(p,x);
>> plot(x,y,'-b',x0,y0,'ro')