遗传算法解决二维排布（典型NP难题）（JS源码），详细探究GA原理

上源码百度云：

 

 

链接：https://pan.baidu.com/s/1gcbPTztzzdK1GkDN-bg3YQ
提取码：asuj
 

 之前写过完全解析版本的遗传算法相关内容，传送门：https://blog.csdn.net/qq_36187544/article/details/84027832

本篇文章对GA在进一步思考分析，不涉及基础内容。

 

首先把问题描述一下：在一定空间中有散落的零件，形状大小各异，想让其最紧凑的排布节省空间。比如下图

实际问题出自增材制造中零件二维贴装排布问题，是一种典型的NP难题。

 

问题的遗传算法三要素分析：

算法分析：

1.适应度函数

由于canvas不提供既有的面积计算或者重叠度分析，所以采用点阵方式进行搜索查询—将平面直角坐标系与边界条件构成一个区间范围，如200×200的区间范围内将其4万个整点作为计算点，遍历循环搜索每个点是否被覆盖。搜索被覆盖的点集最大值，作为最紧凑区域的坐标最小值，计算最紧凑面积，取面积的倒数作为适应度得分。

适应度函数是通过遍历整点坐标返回有无覆盖值来判定图样达到的最大坐标，得到最小紧凑面积。这样遍历的优势在于可以控制精度，比如，要求零件与零件之间最小距离为2mm，取点的时候就可以取以1为间隔取点，最小取点间隔为(正方形对角线长)。间距越小精度越好，得到的排布更加优秀，但是计算时间成倍增长。 

2.轮盘赌选择策略

每一个个体经过适应度函数都能计算出一个适应度分值，对分值采取轮盘赌选择的方式，让每个个体都有概率被选择，从而保留了基因多样性，同时得分高的个体被选中几率更大，符合优胜劣汰的原则。

对于遗传算法种选择阶段，一般有胜者为王策略，平均策略，轮盘赌策略，这里采用轮盘赌策略的原因是轮盘赌策略能保留基因的多样性同时维持优胜劣汰原则。对于二维贴装优化问题而言，种群的基因数据对得到最优解的影响是巨大的，通过概率我们知道在200×200的区域中尽可能的靠近原点、使排布紧凑是一件小概率事件，同时由于淘汰子代机制的存在，得到一个合格的、紧凑的局部最优解是不容易的，所以保持基因多样性是必要的，不可减少的。而平均策略更容易保证基因的多样性，甚至不会淘汰一个比较劣质的基因，但这样同样是不合常理的。就本例而言，坐标值越大对应的基因一定程度上是越劣质的基因，如果一直保留这种劣质基因，反而不容易得到更加优秀的局部最优解。

所以，从机理上出发，在进行二维贴装优化时，采用轮盘赌策略有助于保持基因多样性同时淘汰部分劣质基因，其目的都是为了更高效、更合理的贴近最紧凑布局即最优解。

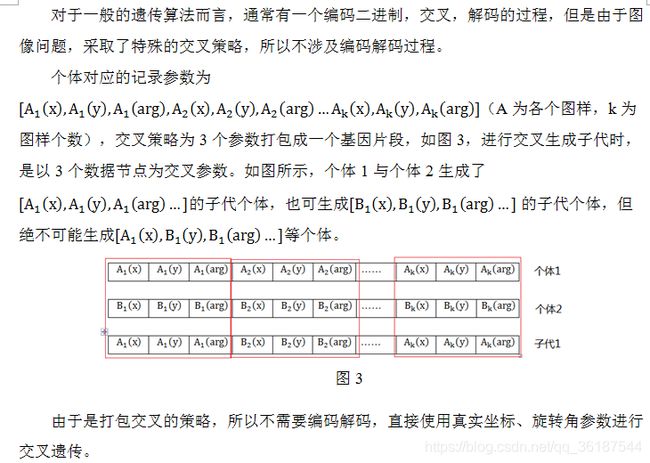
3.交叉

 

 

 

 

在TSP问题中将基因编码成二进制并交叉生成新基因，这样产生的基因会携带随机性，又因样本空间较小，所以具有良好的性质。但在该问题中，若以此方法产生新坐标位置，那就完全生成了新坐标参数变量的图样，使得每代随机性过大，且与父代关系较小。更重要的是，由于样本空间过大，所以随机生成的数据更具有不可预料性。

所以这里以图样为基本单位，视每个图样为一个基本基因，子代拥有父系节点部分图样拥有母系节点部分图样，组成完整基因型，同时，不需要编码解码过程。

4.变异策略的选择

变异是为了提供跳出局部最优解找到全局最优解的方法，这里的变异从图样为基本单位出发是为了以图样为基本单位做改变。若以图样的x,y,arg变量出发做改变将会带来弊端：只做x变动会使图样变成在y方向上平移变化，若只做y变动会使图样变成在x方向上平移变化，若只做旋转角arg变化会使图样绕中心旋转，都过于片面。所以采用用新的3个随机数代替图样基本坐标，以图样作为基本单位，使变异更加合理、全面。

同时，这种变异策略是比较保守的变异策略，变异时只改变某个个体的某组基因即某个图样，若采用激进的变异方法，可同时变异多组（多个图样），这样会使变异进程迅速提高，但同样，可能更容易丢失某些基因。 

5. 记录当前最优解策略的选择

定义一个全局变量，记录当前获取的最优解，这个最优解在选择交叉遗传变异中是不改变的，相当于子代中有一个个体就是父代最优个体。当子代中出现了比这个最优个体更加优秀的个体时，更新这个最优个体。这样就保证了子代的最优解至少不会劣于父代最优解。

因为交叉、变异策略的存在，所以可能导致子代劣于父代，但是这是被允许的，且是较小概率的事件，但是这样一来就可能存在由于交叉、变异将当前最佳个体即最优解迭代消失，这是不被允许的，所以结合禁忌搜索算法中禁忌表思想，将最优个体记录下来，不参加交叉变异等过程，即保证子代最优解至少与父代最优解相同。

 

 

遗传算法解决二维排布问题的局限和缺点：

（1）利用环境、工具的局限性：利用HTML中JS和canvas编写的内容，由于这是纯前端，这不是一种稳定的环境，且执行速度较慢，易崩溃，假死。在大量长时间计算后可能导致参数丢失，结果错误。

（2）适应度函数的局限性：由于不提供既有的算法进行面积计算，所以采用遍历点集的模式，但是这样每次的循环都要上万次，计算量过大，可以发现在改变适应度函数遍历点集个数后，运行时间变动非常大。

（3）遗传算法的局限性：遗传算法是一种基于种群的算法，所以就要求种群的基因型尽可能丰富，若基因型的全部可能数据量较小，那使用遗传算法就容易求得最优解。但是本问题模型的基因空间过于庞大，此时是200×200的空间，根据概率学的思想，穷尽每种情况近乎不可能，即使我们定义最小精度为1mm，4万个点集带来的计算量同样不容小觑。

同时，从概率的角度看待并行嵌套，以圆环和小圆为例，若想使圆环和小圆实现并行嵌套，要求圆环和小圆同心，或者近似同心，也就是说要求在随机生成点时，欲使两个点的坐标近似相等，假设在200×200空间中圆环半径为20，内部空心区域为15，小圆半径为10，则两圆心距离差不超过5，概率为25π/40000×100%=0.19634954%。这种概率是极小的，也就是说种群大小达到500时才会产生距离差不超过5的同心或近似同心情况。所以，并行嵌套时可能的情况，但是概率上较低。

遗传算法中种群大小对最后得到的局部最优解的影响是巨大的，在AM多件生产二维贴装问题上的GA是基于图样为基本单位的，所以如果初代种群能够穷尽图样的排布方式，甚至不

 

需要变异，在经过足够多的迭代次数后一定能获取最优解。问题就在这里，图样的排布在二维平面的方式过于多样化，数量过于庞大，在种群大小为30，精度为1mm的情况下，迭代一次需要10分钟，如果种群数量再增加，计算时间将超过预期。

 

这是整个算法中遇到的最大问题，种群大小与计算时间的冲突，种群大小过小，得到的最优解很差，种群过大，计算时间过长，且种群大就要求迭代次数越多，才能达到一定的收敛性的结果。

 

遗传算法作为解决组合优化问题的一种方法，是模拟进化论的一种方法，每一个步骤在实际问题中都有其隐含意义，多加思考才能对算法进行优化升级。