深度学习中的模型优化(SGD、Momentum、Nesterov、AdaGrad、Adadelta、RMSProp以及Adam)
随机梯度下降
Batch Gradient Descent(BGD)
BGD在训练中,每一步迭代都是用训练集中的所有数据,也就是说,利用现有参数对训练集中的每一个输入生成一个估计输出,然后跟实际输出比较,统计所有误差,求平均以后得到平均误差,并以此作为更新参数的依据.
- 优点: 由于每一步都利用了训练集中的所有数据,因此当损失函数达到最小值以后,能够保证此时计算出的梯度为0,换句话说,就是能够收敛(曲线比较平滑),因此,使用BGD时不需要逐渐降低学习率.
- 缺点: 由于每一步都要用到所有训练数据,因此随着数据集的增大,运行速度会越来越慢.
SGD与MBGD
MBGD是指在训练中,每次使用小批量(一个小批量训练m个样本)的随机采样进行梯度下降.训练方法与BGD一样,只是BGD最后对训练集的所有样本取平均,而MBGD只对小批量的m个样本取平均.SGD是指在训练中每次仅使用一个样本.MBGD与SGD统称为SGD.因为小批量不能代表整个训练集,使得梯度估计引入噪声源,因此SGD并不是每次迭代都向着整体最优化方向.虽然SGD包含一定的随机性(表现为损失函数的震荡),但是从期望来看,它是等于正确的导数的(表现为损失函数有减小的趋势).
- 优点: 训练速度比较快
- 优点: 在样本数量较大的情况下,可能只用到了其中一部分数据就完成了训练,得到的只是局部最优解.另外,小批量样本的噪声较大,所以每次执行梯度下降,并不一定总是朝着最优的方向前进.
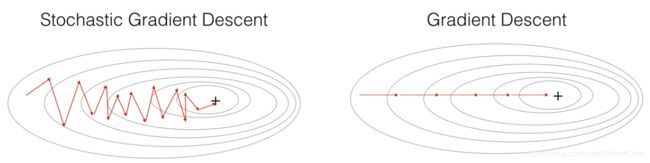
参数更新
{ v t = − η ▽ θ J ( θ t ) θ t = θ t − 1 + v t \left \{ \begin{array}{l}{\boldsymbol{v}_{t}=-\eta \triangledown_\theta J\left(\boldsymbol{\theta}_{t}\right) } \\ {\boldsymbol{\theta}_{t} =\boldsymbol{\theta}_{t-1}+\boldsymbol{v}_{t}}\end{array} \right. {vt=−η▽θJ(θt)θt=θt−1+vt
其中, η \eta η代表学习率, θ t \theta_t θt表示 t t t时刻的参数, ▽ θ J ( θ t ) \triangledown _\theta J(\theta_t) ▽θJ(θt)代表参数 θ \theta θ在 t t t时刻的导数, v t v_t vt代表参数的更新速度。
Momentum
在训练中,采取的策略与SGD一样,不同的是学习率的更新方式。动量的参数更新方式为:
{ v t = − η ▽ θ J ( θ t ) + α v t − 1 θ t + 1 = θ t + v t \left \{ \begin{array}{l}{\boldsymbol{v}_{t}=-\eta \triangledown_\theta J\left(\boldsymbol{\theta}_{t}\right)+\alpha \boldsymbol{v}_{t-1}} \\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. {vt=−η▽θJ(θt)+αvt−1θt+1=θt+vt
α \alpha α一般取值0.9.
直观理解为:
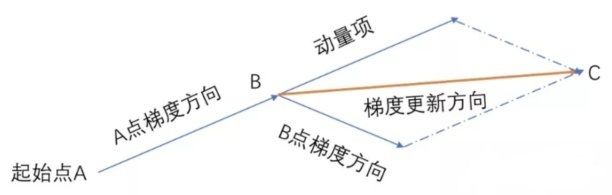
动量方法旨在加速学习(加快梯度的下降速度),特别是处理高曲率、小但一致的梯度,或是带噪声的梯度。动量算法累积了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。
|
|
动量SGD算法引入 α v t − 1 \alpha \boldsymbol{v}_{t-1} αvt−1使每一次的参数更新方向不仅仅取决于当前位置的梯度,还受到上一次参数更新方向的影响(如上图所示)。在某一维度上,当梯度方向不变时,更新速度变快,当梯度方向有所改变时,更新速度变慢,从而加快收敛速度,减少震荡。
带有动量的SGD的优点:
- 加快收敛速度
- 抑制梯度下降时上下震荡的情况
- 通过局部极小点
分析:假设任意时刻参数的梯度均为 g t = ▽ θ J ( θ t ) = g 0 g_t=\triangledown_\theta J\left(\boldsymbol{\theta}_{t}\right)=g_0 gt=▽θJ(θt)=g0,则使用SGD时, t t t时刻的梯度 g t S G D = g 0 g^{SGD}_t=g_0 gtSGD=g0,Momentum算法的梯度 g t m o m = ( α t − 1 + α t − 2 + . . . + α + 1 ) g 0 = 1 − α t 1 − α g 0 g^{mom}_t=(\alpha^{t-1}+\alpha^{t-2}+...+\alpha+1)g_0=\frac{1-\alpha^{t}}{1-\alpha}g_0 gtmom=(αt−1+αt−2+...+α+1)g0=1−α1−αtg0.当 t → + ∞ t\rightarrow +\infty t→+∞,因 α < 1 \alpha<1 α<1,所以 α t → 0 \alpha^t\rightarrow 0 αt→0,所以 g t m o m → 1 1 − α g 0 g_t^{mom}\rightarrow \frac{1}{1-\alpha}g_0 gtmom→1−α1g0,当 α = 0.9 \alpha=0.9 α=0.9时,Momentum更新速度是SGD的10倍
Nesterov(NAG)
Nesterov动量是Momentum的变种,即在计算参数梯度之前,前瞻一步,超前一个动量单位处: θ t + γ v t − 1 \theta_t + \gamma v_{t-1} θt+γvt−1,Nesterov动量可以理解为往Momentum动量中加入了一个校正因子。参数更新公式为:
{ v t = − η ▽ θ J ( θ t + γ v t − 1 ) + α v t − 1 θ t + 1 = θ t + v t \left \{ \begin{array}{l}{\boldsymbol{v}_{t}=-\eta \triangledown_\theta J\left(\boldsymbol{\theta}_{t}+\gamma \boldsymbol{v}_{t-1}\right)+\alpha \boldsymbol{v}_{t-1}} \\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. {vt=−η▽θJ(θt+γvt−1)+αvt−1θt+1=θt+vt
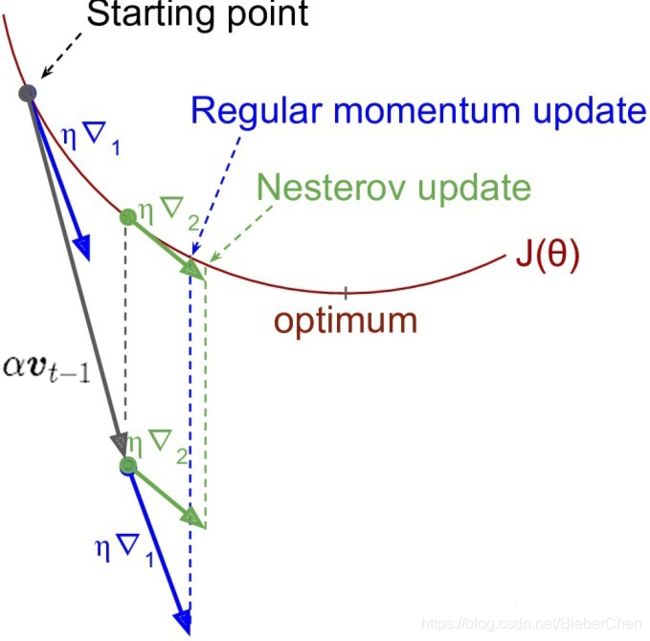
Momentum动量与Nesterov动量的对比如下图所示,其中 η ▽ 1 \eta \triangledown_1 η▽1代表A节点 ( θ t \theta_t θt)的梯度, η ▽ 2 \eta \triangledown_2 η▽2代表B节点( θ t + γ v t − 1 \theta_{t}+\gamma \boldsymbol{v}_{t-1} θt+γvt−1的梯度),灰色实线代表 t − 1 t-1 t−1时刻的速度 α v t − 1 \alpha v_{t-1} αvt−1.
|
|
注意:图中的 η ▽ 1 以 及 η ▽ 2 \eta \triangledown_1以及\eta \triangledown_2 η▽1以及η▽2应该为 − η ▽ 1 -\eta \triangledown_1 −η▽1、 − η ▽ 2 -\eta \triangledown_2 −η▽2因为梯度方向是增长速度最快的方向,而图中所示为梯度的反方向,所以应该为 − η ▽ 1 -\eta \triangledown_1 −η▽1、 − η ▽ 2 -\eta \triangledown_2 −η▽2.
Nesterov动量相对于Momentum多了一个本次梯度相对上次梯度的变化量,这个变化量本质上是对目标函数二阶导的近似,由于令了二阶导的信息,Nesterov动量算法才会比Momentum具有更快的收敛速度。
AdaGrad
AdaGrad其实是对学习率进行了约束,AdaGrad独立地适应所有模型参数的学习率,缩放每个参数反比于其它所有梯度历史平方值总和的平方根。损失较大偏导的参数相应地拥有一个快速下降的学习率,而较小偏导的参数在学习率上有相对较小的下降。净效果是在参数空间中更为平缓的倾斜方向会取得更大的进步。参数更新公式为:
{ g t = ▽ θ J ( θ t ) n t = n t − 1 + g t 2 v t = − η n t + ϵ g t θ t + 1 = θ t + v t \left \{ \begin{array}{l}{ g_t=\triangledown_\theta J(\theta_t)}\\ {n_t=n_{t-1}+g_t^2} \\ {\boldsymbol{v}_{t}=-\frac{\eta}{\sqrt{n_t+\epsilon}}g_t } \\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. ⎩⎪⎪⎨⎪⎪⎧gt=▽θJ(θt)nt=nt−1+gt2vt=−nt+ϵηgtθt+1=θt+vt
其中, ϵ \epsilon ϵ是个很小的数,用来保证分母非0。对 g t g_t gt从1到t进行一个递推形成一个约束项regularizer——- 1 n t + ϵ \frac{1}{\sqrt{n_t+\epsilon}} nt+ϵ1。
优点:
前期 g t g_t gt较小的时候, 1 n t + ϵ \frac{1}{\sqrt{n_t+\epsilon}} nt+ϵ1较大,梯度更新较大,可以解决SGD中学习率一直不变的问题;后期 g t g_t gt较大的时候, 1 n t + ϵ \frac{1}{\sqrt{n_t+\epsilon}} nt+ϵ1较小,能够约束梯度.适合处理稀疏梯度.
缺点:
由公式可以看出,AdaGrad依赖于人工设置一个全局学习率?,当 η \eta η设置过大时,使regularizer过于敏感,对梯度的调节太大。在中后期,分母上梯度平方的累加将会越来越大,gradient→0,网络的更新能力会越来越弱,学习率会变的极小,使得训练提前结束。为了解决这样的问题,又提出了Adadelta算法。
Adadelta
Adadelta是对AdaGrad的扩展,AgaGrad会累加所有历史梯度的平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。参数更新方式为:
{ g t = ▽ θ J ( θ t ) n t = γ n t − 1 + ( 1 − γ ) g t 2 v t = − η n t + ϵ g t θ t + 1 = θ t + v t \left \{ \begin{array}{l}{ g_t=\triangledown_\theta J(\theta_t)}\\ {n_t=\gamma n_{t-1}+(1-\gamma)g_t^2}\\ {\boldsymbol{v}_{t}=-\frac{\eta}{\sqrt{n_t+\epsilon}}g_t } \\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. ⎩⎪⎪⎨⎪⎪⎧gt=▽θJ(θt)nt=γnt−1+(1−γ)gt2vt=−nt+ϵηgtθt+1=θt+vt
但是,此时Adadelta其实仍然依赖于全局学习率,因此,又做了一些处理,新的参数更新方式为:
{ g t = ▽ θ J ( θ t ) E ∣ g 2 ∣ t = ρ × E ∣ g 2 ∣ t − 1 + ( 1 − ρ ) × g t 2 v t = − ∑ r = 1 t − 1 v r E ∣ t 2 ∣ t + ϵ g t θ t + 1 = θ t + v t \left \{ \begin{array}{l}{ g_t=\triangledown_\theta J(\theta_t)}\\ {E|g^2|_t=\rho \times E|g^2|_{t-1}+(1-\rho)\times g_t^2}\\ {v_t=-\frac{\sqrt{\sum_{r=1}^{t-1}}v_r}{\sqrt{E|t^2|_t+\epsilon}}g_t}\\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧gt=▽θJ(θt)E∣g2∣t=ρ×E∣g2∣t−1+(1−ρ)×gt2vt=−E∣t2∣t+ϵ∑r=1t−1vrgtθt+1=θt+vt
新的参数更新方式,不依赖于全局学习率,并且,训练初中期,加速效果不错,很快;训练后期,反复在局部最小值附近抖动。
RMSprop
RMSprop可以算作Adadelta的一个特例:当 ρ = 0.5 \rho=0.5 ρ=0.5时, E ∣ g 2 ∣ t = ρ × E ∣ g 2 ∣ t − 1 + ( 1 − ρ ) × g t 2 E|g^2|_t=\rho \times E|g^2|_{t-1}+(1-\rho)\times g_t^2 E∣g2∣t=ρ×E∣g2∣t−1+(1−ρ)×gt2就变为了求梯度平方和的平均数。
如果再求根的话,就变成了RMS(均方根): R M S ∣ g ∣ t = E ∣ g 2 ∣ t + ϵ RMS|g|_t=\sqrt{E|g^2|_t+\epsilon} RMS∣g∣t=E∣g2∣t+ϵ。RMSprop的参数更新方式为:
{ g t = ▽ θ J ( θ t ) E ∣ g 2 ∣ t = ρ × E ∣ g 2 ∣ t − 1 + ( 1 − ρ ) × g t 2 R M S ∣ g ∣ t = E ∣ g 2 ∣ t + ϵ v t = − η R M S ∣ g ∣ t g t θ t + 1 = θ t + v t \left \{ \begin{array}{l}{ g_t=\triangledown_\theta J(\theta_t)}\\ {E|g^2|_t=\rho \times E|g^2|_{t-1}+(1-\rho)\times g_t^2} \\ {RMS|g|_t=\sqrt{E|g^2|_t+\epsilon}}\\ {\boldsymbol{v}_{t}=-\frac{\eta}{RMS|g|_t }g_t} \\ {\boldsymbol{\theta}_{t+1} =\boldsymbol{\theta}_{t}+\boldsymbol{v}_{t}}\end{array} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧gt=▽θJ(θt)E∣g2∣t=ρ×E∣g2∣t−1+(1−ρ)×gt2RMS∣g∣t=E∣g2∣t+ϵvt=−RMS∣g∣tηgtθt+1=θt+vt
特点: (1)RMSprop依然依赖于全局学习率;(2)RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间;(3)适合处理非平稳目标 - 对于RNN效果很好
Adam
Adam优化器结合了AdaGrad与RMSProp两种算法的优点。对梯度的一阶距估计 m t m_t mt(即梯度的均值)和二阶距估计 n t n_t nt(即梯度的未中心化的方差)进行综合考虑,计算出更新步长。更新方式为:
{ g t = ▽ θ J ( θ t ) m t = β 1 m t − 1 + ( 1 − β 1 ) g t v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 m t ^ = m t 1 − β 1 t v ^ t = v t 1 − β 2 t θ t + 1 = θ t − η v ^ t + ϵ m ^ t \left \{ \begin{array}{l}{ g_t=\triangledown_\theta J(\theta_t)}\\ {m_t=\beta_1m_{t-1}+(1-\beta_1)g_t}\\ {v_t=\beta_2v_{t-1}+(1-\beta_2)g_t^2}\\ {\hat{m_t}=\frac{m_t}{1-\beta_1^t}}\\ {\hat{v}_t=\frac{v_t}{1-\beta_2^t}}\\ {\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_{t}-\frac{\eta}{\sqrt{\hat{v}_t+\epsilon}}\hat{m}_t}\\ \end{array} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧gt=▽θJ(θt)mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2mt^=1−β1tmtv^t=1−β2tvtθt+1=θt−v^t+ϵηm^t
注:所有的 t t t均表示 t t t时刻。 m t m_t mt、 n t n_t nt分别是梯度的一阶距估计和二阶距估计,可以看做是对期望 E ∣ g t ∣ 、 E ∣ g t 2 ∣ E|g_t|、E|g_t^2| E∣gt∣、E∣gt2∣的估计; m ^ t 、 n ^ t \hat{m}_t、\hat{n}_t m^t、n^t是对 m t m_t mt、 n t n_t nt的校正,这样可以近似为对期望的无偏估计。
优点:
- 实现简单,计算高效,对内存需求少
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有很好的解释性,且通常无需调整或仅需很少的微调
- 更新的步长能够被限制在大致的范围内(初始学习率)
- 能自然地实现步长退火过程(自动调整学习率)
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
参考资料:
https://zhuanlan.zhihu.com/p/73264637
https://zhuanlan.zhihu.com/p/60088231
https://blog.csdn.net/u012759136/article/details/52302426