机器学习笔记(吴恩达)(一)--单变量线性回归
机器学习笔记(吴恩达)(一)--单变量线性回归
- 场景描述
- 概念介绍
- 假设函数
- 代价函数
- 代价函数详解
- 代价函数与参数$\Theta$的关系
- 梯度下降法
个人blog https://verbf.github.io/
场景描述
我们有关于房屋面积和房屋价格的数据集,现在想拟合一条直线通过房屋的面积来预测房屋价格。这条直线应该尽可能的符合已有的数据。
概念介绍
假设函数
这里我们简单的假设该直线的方程为
h ( x ) = Θ x h(x) = \Theta x h(x)=Θx
其中x表示房屋的面积,h(x) 表示预测出的房价。有了这个假设函数我们就可以预测房价了。
那么参数 Θ \Theta Θ应该怎么确定呢?这里我们需要用到代价函数。
代价函数
这里先给出代价函数的表达式
J ( Θ ) = 1 2 m ∑ i = 1 m ( h Θ ( x ( i ) ) − y ( i ) ) 2 J(\Theta)=\frac{1}{2m}\sum_{i=1}^{m}{({h_\Theta}({x}^{(i)})-{y}^{(i)})}^{2} J(Θ)=2m1i=1∑m(hΘ(x(i))−y(i))2
其中
x ( i ) {x}^{(i)} x(i)表示第i个数据样本中房屋的面积
h Θ ( x ( i ) ) {h_\Theta}({x}^{(i)}) hΘ(x(i))表示使用假设函数预测房屋面积 x ( i ) {x}^{(i)} x(i)的得到的房屋价格
y ( i ) {y}^{(i)} y(i)表示真实的房屋价格
这里我们选择使用均方误差作为衡量预测结果与真实值的偏差。最前面的 1 2 \frac{1}{2} 21 只是为了计算方便无需在意。
我们所要做的就是改变 Θ \Theta Θ的值,使得代价函数J ( Θ ) (\Theta) (Θ)的值最小,当找到一个 Θ \Theta Θ使得代价函数的值最小时,我们就确定了参数 Θ \Theta Θ。即我们的优化目标:
m i n i m i z e J ( Θ ) minimizeJ(\Theta) minimizeJ(Θ)
为什么说我们要找的 Θ \Theta Θ会使代价函数取得最小值呢?接下来举例说明。
代价函数详解
代价函数与参数 Θ \Theta Θ的关系
假设我们的数据集中有三个样本点 (1,1) , (2,2) , (3,3)
我们可以使用无数条直线来拟合这些样本,但很显然只有当 Θ = 1 \Theta = 1 Θ=1时,即 y = x y=x y=x 这条直线有最好预测效果。
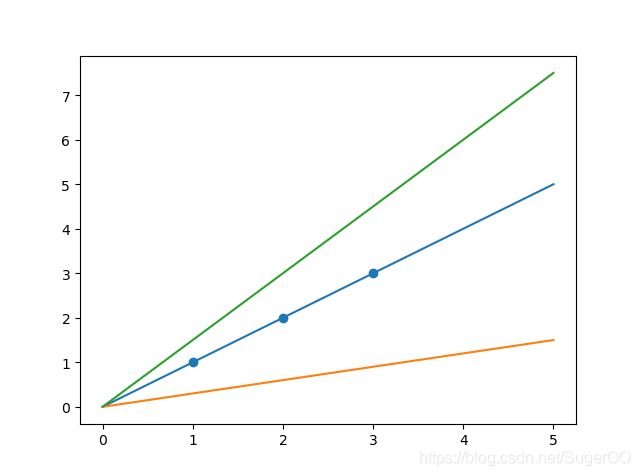
然后我们将不同的 Θ \Theta Θ值带入代价函数,计算其结果:
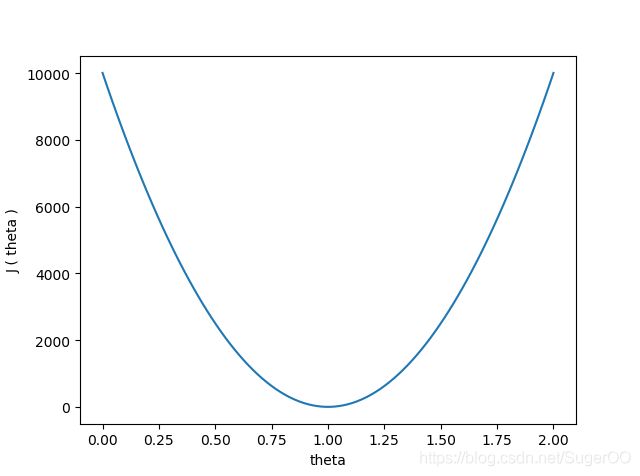
从图像上可知,当代价函数的图像在最低点时,对应 Θ \Theta Θ的值,就是最佳的结果。
通过这个例子不难发现,只要我们求出代价函数的最小值,就可找到我们想要的参数 Θ \Theta Θ的值。
那么代价函数的最小值应该怎么求呢?在数学上有许多方法可以解决这个问题,这里我们使用梯度下降法来求代价函数的最小值。
梯度下降法
下图是使用梯度下降法求解 Θ \Theta Θ的步骤,开始时我们随机赋给 Θ \Theta Θ一个初值,重复执行下面的步骤更新 Θ \Theta Θ的值。执行一定次数,当 Θ \Theta Θ的值基本不再变化时,我们就求出了 Θ \Theta Θ的最后结果。
Θ = Θ − α ∂ J ( Θ ) ∂ Θ \Theta = \Theta - \alpha\frac{\partial{J(\Theta)}}{\partial\Theta} Θ=Θ−α∂Θ∂J(Θ)
其中关键的步骤是对代价函数求 Θ \Theta Θ的偏导,这可以理解为在求某一点的斜率。
当 Θ \Theta Θ的值大于最终结果时, Θ \Theta Θ的取值在最终结果的右边,对应点的斜率大于0,即求出的偏导值大于0, Θ \Theta Θ减去一个大于0的数变小。
当 Θ \Theta Θ的值小于最终结果时, Θ \Theta Θ的取值在最终结果的左边,对应点的斜率小于0,即求出的偏导值小于0, Θ \Theta Θ减去一个小于0的数后变大。
当 Θ \Theta Θ的值越接近最终结果时,导数越接近0, Θ \Theta Θ变化的速度也越慢。
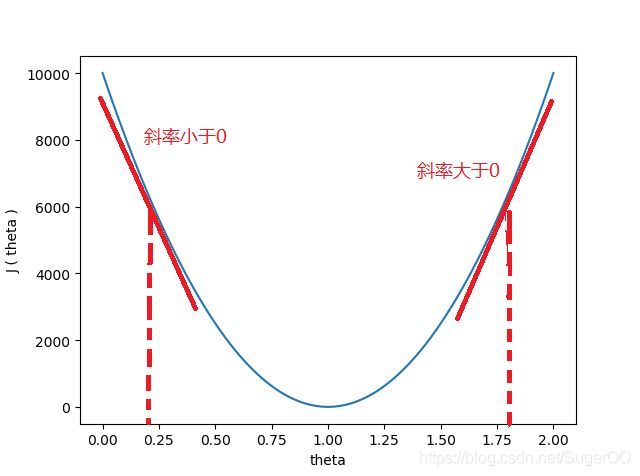
其中 α \alpha α 是学习率,它的大小会改变 Θ \Theta Θ的改变速度,但取值不能太大,否则会造成 Θ \Theta Θ无法收敛。