模多项式求逆python实现
模多项式求逆python实现
1、原理:
2、编程要求
不使用科学计算库
3、代码:
"""
在Zp域上实现模多项式求逆
Date:2019/12/24
@author:Zhai
"""
#提取多项式的方幂信息及对应系数,返回对应列表,形如:[2,3,1,0,1]对应多项式2x^4+3x^3+x^2+1
def extract_info(str_polynimial):
length=len(str_polynimial)
add=1 #记录加号位置
for i in range(length):
if i==0: #获取x的最高次幂指数及其系数
j=0
while(j!=length and str_polynimial[j]!='x'):
j+=1
if j+1==length or str_polynimial[j+1]!='^':
index_list = [0] *2
str_coefficient = "".join([str(item) for item in str_polynimial[0:j]])
if str_coefficient=="":
str_coefficient='1'
index=1
index_list[index] = int(str_coefficient)
elif str_polynimial[j+1]=='^':
k=j+2
while(k!=length and str_polynimial[k]!='+' and str_polynimial[k]!='-'):
k+=1
str_index = "".join([str(item) for item in str_polynimial[j+2:k]])
highest_index = int(str_index) # 获取最高次幂指数
index_list = [0] * (highest_index + 1)
index = highest_index
if j == 0: # 首项系数为1的情况下
index_list[index] = 1
else:
str_coefficient = "".join([str(item) for item in str_polynimial[0:j]])
index_list[index] = int(str_coefficient)
elif str_polynimial[i]!='+' and str_polynimial[i]!='-':
continue
else:
j = i
while (j!=length and str_polynimial[j] != 'x'):
j += 1
#截取x某一方幂前的系数
str_coefficient = "".join([str(item) for item in str_polynimial[i+1:j]])
if str_coefficient=="": #如果str_coefficient未截取到字符串,证明该项系数为1,令str_coefficient='1'
str_coefficient='1'
if str_polynimial[i]=='-': #如若系数为负,更正系数
str_coefficient="-"+str_coefficient
#下面确定并截取x的方幂次数
if j==length: #如果已遍历至字符串末位,证明x对应方幂为0
str_index='0'
elif (j+1)==length or str_polynimial[j+1]=='+'or str_polynimial[j+1]=='-': #如果x紧接着的字符为’+‘或此时x为最后一个字符,则证明该x对应的方幂次数为1
str_index = '1'
else:
k=j+2
while(k!=length and str_polynimial[k]!='+' and str_polynimial[k]!='-'):
k+=1
#while语句执行完后,str_polynimial[k]='+'
str_index="".join([str(item) for item in str_polynimial[j+2:k]]) #截取x对应的方幂次数
#修改列表对应参数
index_list[int(str_index)]=int(str_coefficient)
index_list.reverse()
return index_list
#将列表转换为多项式,如[2,1,0,12]将被转换为字符串"2x^3+x^2+12"
def translation(list):
str_polynimial=""
for i in range(len(list)):
if list[i]==0:
continue
index=len(list)-i-1 #获取方幂次数
coefficient=list[i] #获取对应x某一方幂的系数
if index==0:
string=str(coefficient)
elif index==1:
if coefficient==1:
string = 'x'
else:
string=str(coefficient)+'x'
else:
if coefficient==1:
string = 'x' + '^' + str(index)
else:
string=str(coefficient)+'x'+'^'+str(index)
if i==0 or list[i]<0:
str_polynimial=str_polynimial+string
elif list[i]>0:
str_polynimial=str_polynimial+'+'+string
if str_polynimial=="":
str_polynimial="0"
return str_polynimial
#定义多项式列表与数的乘法,参数list为被乘的多项式列表,a为int型的乘数。计算数域为Zp
def Multiplication(list,a,p):
result=[]
for i in range(len(list)):
result.append(list[i]*a%p)
return result
#定义多项式与多项式的乘法,参数list1,list2均为多项式的列表表示法。计算数域为Zp
def Multiplication2(list1,list2,p):
a=list1.copy()
b=list2.copy()
result=[0]
for i in range(len(b)):
product=Multiplication(a,b[i],p)
product.extend([0]*(len(b)-1-i))
result=Add(result,product,p)
return result
#定义多项式列表表示的减法,要求参数list1与list2等长,返回结果仍为等长的列表。计算数域为Zp
def Subtraction(list1,list2,p):
a=list1.copy()
b=list2.copy()
result=[]
for i in range(len(a)):
result.append((a[i]-b[i])%p)
return result
#计算数域为Zp
def Subtraction2(list1,list2,p):
a=list1.copy()
b=list2.copy()
if len(a)<len(b):
a.reverse()
a.extend([0]*(len(b)-len(a)))
a.reverse()
elif len(a)>len(b):
b.reverse()
b.extend([0] * (len(a) - len(b)))
b.reverse()
result=Subtraction(a,b,p)
return result
#定义多项式的加法,默认参数list1、list2不等长
def Add(list1,list2,p):
a=list1.copy()
b=list2.copy()
result=[]
if len(a)>len(b):
b.reverse()
b.extend([0]*(len(a)-len(b)))
b.reverse()
max=len(a)
else:
a.reverse()
a.extend([0]*(len(b)-len(a)))
a.reverse()
max=len(b)
for i in range(max):
result.append((a[i]+b[i])%p)
for j in range(len(result)): # 除去列表最左端无意义的0
if result[0] == 0:
result.remove(0)
else:
break
return result
#实现多项式带余除法,参数list1、list2均为列表,返回多项式商q的列表与余式r的列表
def Division(list1,list2,p):
#此处注意要深拷贝,浅拷贝会修改传进来的参数值
r=list1.copy()
b=list2.copy()
length=len(r) #记录初始被除多项式位数
if len(r)<len(b):
return [0],list1
q=[0]*(len(r)-len(b)+1)
for i in range(len(q)):
if len(r)>=len(b):
index=len(r)-len(b)+1 #确定所得商是商式的第index位
q[-index] = int(r[0] / b[0])
# 更新被除多项式
b_=b.copy()
b_.extend([0] * (len(r) - len(b)))
b_=Multiplication(b_,q[i],p)
r = Subtraction(r ,b_,p)
for j in range(len(r)): #除去列表最左端无意义的0
if r[0]==0:
r.remove(0)
else:
break
else:
break
return q,r
#扩展欧几里得算法,输入两个多项式列表list1、list2,返回二者的最大公因式列表d,以及满足d=u*list1+v*list2的u和v
#默认list1、list2不等于0
def Extend_Euclid(list1,list2,p):
f=list1.copy()
g=list2.copy()
u_2=[1]
u_1=[0]
v_2=[0]
v_1=[1]
while(g!=[]):
q,r=Division(f,g,p)
u=Subtraction2(u_2,Multiplication2(q,u_1,p),p)
v=Subtraction2(v_2,Multiplication2(q,v_1,p),p)
f,g=g,r
u_2,u_1=u_1,u
v_2,v_1=v_1,v
d,u,v=f,u_2,v_2
return d,u,v
def test():
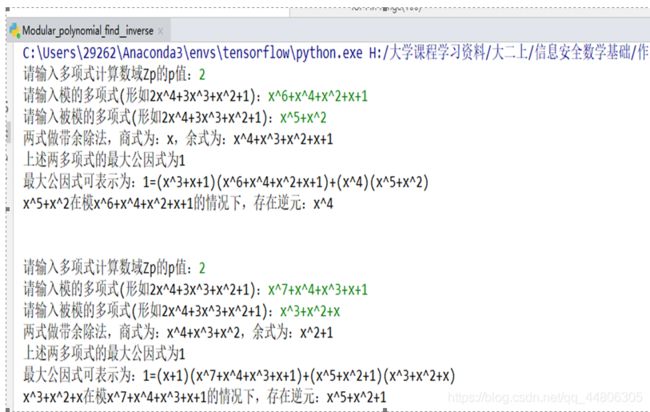
p = int(input("请输入多项式计算数域Zp的p值:"))
str_polynimial = input("请输入模的多项式(形如2x^4+3x^3+x^2+1):")
list1 = extract_info(str_polynimial)
str1 = translation(list1)
str_modular = input("请输入被模的多项式(形如2x^4+3x^3+x^2+1):")
list2 = extract_info(str_modular)
str2 = translation(list2)
q, r = Division(list2,list1 ,p)
str_q = translation(q)
str_r = translation(r)
print("两式做带余除法,商式为:"+str_q + ",余式为:" + str_r)
d,v,u=Extend_Euclid(list2,list1,p)
str_d=translation(d)
str_u=translation(u)
str_v=translation(v)
print("上述两多项式的最大公因式为"+str_d )
print("最大公因式可表示为:"+str_d+"=("+str_u+")("+str1+")+("+str_v+")("+str2+")")
print(str2+"在模"+str1+"的情况下,存在逆元:"+str_v)
# for i in range(100):
# test()
# print("\n")
if __name__ == '__main__':
test()