二叉树的遍历
二叉树是半线性结构,通过按照事先约定的某种规则,即在二叉树的节点之间定义某种线性次序,转化为线性结构,手法就是遍历。
遍历:按照某种次序访问树中的各节点,每个节点被访问恰好一次。

二叉树结点结构
public class BinNode {
int value;
BinNode left;
BinNode right;
public BinNode(int value) {
this.value = value;
}
@Override
public String toString(){
return "value: "+value;
}
}
访问函数
public void visit(BinNode node){
System.out.print(node.value+" ");
}
一、二叉树的先序遍历
先序遍历的顺序是::先自上而下访问左侧链上的节点,再自下而上访问它们的右子树
递归遍历
二叉树的定义就是递归,按照定义很容易写出递归代码。
public class BinNode {
int value;
BinNode left;
BinNode right;
public BinNode(int value) {
this.value = value;
}
@Override
public String toString(){
return "value: "+value;
}
public void visit(BinNode node){
System.out.print(node.value+" ");
}
public static void preOrderRecursive(BinNode node) {
if (node == null) {//如果为空树则返回
return;
}
visit(node);
preOrderRecursive(node.left);
preOrderRecursive(node.right);
}//T(n)=O(1)+T(a)+T(n-a-1) = O(n)
}
此算法时间复杂度是:T(n)=O(1)+T(a)+T(n-a-1) = O(n)
这已经是不能再好的结果了,然而只具有渐进(recursing)意义,在实际的运行过程当中因为递归程序的普遍机制并不可能做到针对具体的问题来量体裁衣,而只能采用通用的方法,在云兄栈中尽管每一个递归实例都的确对应于一帧,但是因为他们必须具有通用格式,所以不能做到足够的小。而针对于具体的问题,只有我们能够进行精巧的设计完全可以使得每一帧足够小,尽管从递归的意义上面讲,这两种策略所对应的每一帧时间复杂度都可以认为是常数O(1),但是这个常数的差异是巨大的。因此作为树算法的一个重要基石,遍历算法非常有必要从递归形式改写为迭代形式,同时从学习者角度经过这样的改写之后我们也可以对整个遍历算法的过程及原理获得更加深刻的认识。
稍加观察发现此处的两处递归调用都非常类似于我们常用的尾(tail)递归。**其特征是递归调用出现在整个递归实例体的尾部。这种递归是很容易化简为迭代形式的。**为此我们只需要引入一个栈。
迭代遍历
改写后的第一个迭代版本如下所示:
public static void preOrderIterate1(BinNode x) {
if (x == null) {//如果为空树则返回
return;
}
Stack s = new Stack<>();//辅助栈
s.push(x);
while (!s.isEmpty()) {
x = s.pop();
visit(x);
if (x.right != null) {
s.push(x.right);
}
if (x.left != null) {
s.push(x.left);
}
}
}
作为初始化我们引入一个辅助栈S,用以存放树节点的位置,即存放对他们的引用
左右孩子的入栈次序:先右后左,因为包括先序遍历在内的所有遍历都必然先遍历左子树,再遍历右子树在这样一个算法模式中对每个节点都是弹出栈的时刻才接受访问,所以根据栈后进先出(LIFO)的特性,自然也就将希望后出栈的右子树先入栈了。
迭代2新思路:先自上而下访问左侧链上的节点,再自下而上访问它们的右子树。

对于任何一颗子树,在起始的若干拍中,接受访问的节点分别是谁,首先是根,然后根的左孩子,根的左孩子的左孩子…一直到null,再进行转移。
定义:对于任何一颗子树,起始于树根的接下来总是沿着左侧分支不断下行的这样一条链称为当前这颗子树的左侧链。迭代2的算法就是沿着这条左侧链展开。
public static void preOrderIterate2(BinNode x) {
if (x == null) {//如果为空树则返回
return;
}
Stack s = new Stack<>();//辅助栈
while (true) {//以(右)子树为单位,逐批访问节点
visitAlongLeftBranch(x, s);
if (s.isEmpty()) {//栈空即退出
break;
}
x = s.pop();//弹出下一子树的根
}
}
public static void visitAlongLeftBranch(BinNode x, Stack s) {
while (x != null) {
visit(x);//访问当前节点
s.push(x.right);//右子树入栈(将来逆序输出)
x = x.left;//沿左侧链下行
}//只有右孩子、null可能入栈-增加判断以删除后者,是否值得?
}
此种写法更容易记忆:
public static void preOrderIterate3(BinNode x) {
Stack s = new Stack<>();//辅助栈
while (true) {//以(右)子树为单位,逐批访问节点
while (x != null) {
visit(x);//访问当前节点
s.push(x.right);//右子树入栈(将来逆序输出)
x = x.left;//沿左侧链下行
}
if (s.isEmpty()) {//栈空即退出,就是没有右子树了
break;
}
x = s.pop();//弹出下一右子树的根
}
}
注意:理解以(右)子树为单位,逐批访问节点,Td-T0。
测试代码如下:
public static void main(String args[]) {
BinNode root = new BinNode(6);
BinNode node0 = new BinNode(0);
BinNode node1 = new BinNode(1);
BinNode node2 = new BinNode(2);
BinNode node4 = new BinNode(4);
BinNode node5 = new BinNode(5);
BinNode node8 = new BinNode(8);
BinNode node9 = new BinNode(9);
node0.left = null;
node0.right = node1;
node4.left = null;
node4.right = node5;
node8.left = null;
node8.right = node9;
node2.left = node0;
node2.right = node4;
root.left = node2;
root.right = node8;
preOrderIterate2(root);
}
二、二叉树的中序遍历
一些定义建立在先序遍历文章的基础之上。
递归遍历:
//中序遍历
public static void inOrderRecursive(BinNode node) {
if (node == null) {//如果为空树则返回
return;
}
inOrderRecursive(node.left);
visit(node);
inOrderRecursive(node.right);
}
迭代遍历:
相对于先序遍历,从递归遍历改写为迭代要难了几分?
因为:此处的递归不是尾递归,对于右子树的遍历还可以称为尾递归。但是对左子树的递归调用因为中间嵌套了对于根节点的访问而严格的不是尾递归。
迭代思路:
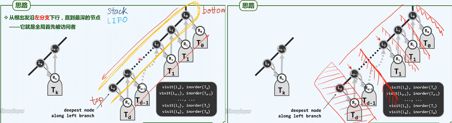
可以理解为左下方侧的节点Ld(和它的右子树)未曾出现过或者已经被访问过,然后访问权被Ld-1…接管。y一句话描述为:访问最左下方节点,访问它的右子树,向上移动一层,再继续重复之。访问它的整个过程存在逆序性,整个访问的起点在根节点处,接受访问的缺少根节点所在的左侧链的末端节点。整个谦让过程是自顶向下的,各节点实际被访问的次序整体而言是一种自下而上的过程。
public static void inOrderIterate(TreeNode x) {
Stack s = new Stack<>();
while (true) {
goAlongLeftBranch(x, s); //从当前节点触发,逐批入栈
if (s.isEmpty()) {//直至所有节点处理完毕
break;
}
x = s.pop(); // node的左子树为空,或者已经遍历(等效于空),故可以
visit(x); // 立即访问之
x = x.right; // /再转向右子树(可能为空,留意处理手法)
}
}
public static void goAlongLeftBranch(TreeNode x, Stack s) {
while (x != null) {//反复入栈沿左分支深入
s.push(x);
x = x.left;
}
}
各种二叉树的迭代遍历算法时间复杂度仍然是O(n),可采用分摊分析判断。
先中后序都不能保证所有的节点按照深度次序进行访问,这三种都有后代先于祖先被访问的现象,称之为逆序。实现这些遍历的时候都借助的栈结构。
三、层次遍历
层次遍历的次序是:自上而下访问各个深度的节点,同样深度的节点中自左向右 。
前提:有根有序树。
在垂直方向按照节点可以划分成若干个等价类,有根性对应的是垂直方向的次序。位于同一深度属于同一等价类内部的所有节点,如何定义次序呢。对于二叉树根据左右的明确定义给出所有的同辈节点的相对次序。这样水平方向和垂直方向的次序都有了,可以在所有的节点之间定义一个整体的次序,进而对其进行遍历。自高向底,自左向右,逐一的访问树中每一个节点,严格满足顺序性。如此定义的遍历策略即层序遍历。
这样的场合与栈对应的数据结构队列就大显身手了。
//层次遍历
public static void levelOrder(BinNode node) {
Queue queue = new LinkedList();//引入辅助队列
queue.offer(node);//根节点入队
while (!queue.isEmpty()) {
BinNode x = ((LinkedList) queue).pollFirst();
visit(x);
if (x.left != null) {
queue.offer(x.left);
}
if (x.right != null) {
queue.offer(x.right);
}
}
}