1.算法入门必知必会：时间复杂度和空间复杂度

时间复杂度分析

时间复杂度与系数无关

如何判断一段代码的时间复杂度，就是直接看他会执行多少次

一、常见的时间复杂度

O(1) Constant Complexity  常数复杂度

下面的都是常数复杂度，与系数无关。打印三次sysout他的时间复杂度也是O(1)

int n = 1
System.out.println("abc is"+n);

int n = 2
System.out.println("abc is"+n);
System.out.println("bdc is"+n);
System.out.println("cdf is"+n);

O(n) Linear Complexity 线性时间复杂度

下面的代码的时间复杂度就是跟随n线性变化的，所以是线性复杂度。

假设下面的有两个并行的for循环，虽然会执行2n次，但是时间复杂度还是O(n),与系数无关

for(int i=1; i<=n; i++){
    System.out.println("i is"+i);
}

O(n^2) N square Complexity 平方复杂度

如下面代码所示：双层嵌套就是 平方时间复杂度

for(int i=1; i<=n; i++){
    for(int j=1; j<=n; j++){
        System.out.println("i" + i + "j" + j);
    }
}

O(n^3) N cubic Complexity 立方复杂度

for(int i=1; i<=n; i++){
    for(int j=1; j<=n; j++){
        for(int k=1; k<=n; j++){
            System.out.println("i" + i + "j" + j);
        }
    }
}

O(K^n) Exponential Growth 指数复杂度

k是一个常数。例如下面的求斐波那契数列的第n项代码，他的时间复杂度就是2的n次方。就属于指数复杂度的。

如果按照下图所示采用了递归的形式，那么他的时间复杂度就是指数级的，非常慢。下面我们会具体分析为什么然是指数级的时间复杂度。

int fib(int n){
    if(n<2) return n;
    return fib(n-1) + fib(n-2)
}

O(log n) Logarithmic Complexity 对数复杂度

如下图代码所示，如果n=4的话下面的代码就只会执行两次，所以这段代码的时间复杂度就是O(log n)

for(int i=1; i

O(n!) Factorial 阶乘复杂度

 

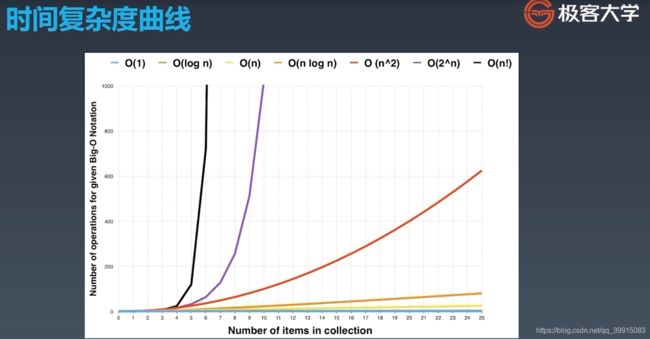
二、常见时间复杂度曲线比较

如下图所示，当N比较小的时候，5以内的时候，不同的时间复杂度都是差不多的。当N开始扩大的时候，指数级的时间复杂度是增长的非常快的。所以说我们在平时工作中写代码的时候，就应该着重注意我们写的代码的时间复杂度情况。如果我们能够通过优化，将时间复杂度从O(n^2)降到O(n)的话，当n非常大的时候，我们能够获得到的收益是非常大的。

1、养成一个习惯：在写完一段程序的时候，去分析自己代码的时间复杂度和空间复杂度。

2、努力让自己成为一个可以用很小时间复杂度去实现代码。

三、例题验证时间复杂度

例题：计算1+2+3+...+n。不同的算法的对应的复杂度

方法一：暴力求解，从1 到n的循环累加.根绝代码可以看到时间复杂度为O(n)

int sum = 0;
for (int i = 1; i <= num ; i++) {
     sum += i;
 }

方法二：求和公式sum = n(n+1)/2.时间复杂度是O(1)。

int sum = n(n+1)/2;

程序的不同方法，最后得到结果一样，但是时间复杂度确实完全不一样的。

因此拿到一个面试题的时候，结局思路可以分为以下四步骤

1、与面试官，确认题目中的所有信息无误

2、想所有可能的解决办法，通过比较找出时间复杂度空间复杂度最有的结果

3、开始写代码

4、测试验证

四、详细分析递归算法的时间复杂度

一般的程序我们在分析时间复杂度的时候，就是看n的大小，总共执行了多少次，但是递归不一样，因为递归是层层嵌套的。那我们这次就通过把递归的执行情况画出来一个树形结构（递归状态树），来分析一下他的时间复杂度。

如下图所示，求菲波那切数列的第n项的值

我们按照上的代码来分析，假设我们现在计算n=6的时候是多少，按照代码的逻辑我们发现，计算6的话，首先我需要计算一个f（5）和f(4),那么我们现在把这个计算过程展开如下图所示：

根据图示我们可以发现有两个特点：

1、每多展开一层，运行的节点数就是上面一层的两倍。

第一层是运行2次-->f(5)、f(4)

第二层就是运行4次-->f(4)、f(3)、f(3)、f(2)

第四层就是运行8次-->f(3)、f(2)、f(2)、f(1)、f(2)、f(1)、f(1)、f(0)

所以我们可以得出，简单的递归求斐波那契数列第N项他的时间复杂度是2^n。指数级的时间复杂度

2、有非常多的重复的节点。

即f(4)、f(3)等都被计算了很多次。所以我们平时写这个算法题的时候不要这么写，可以加上一个缓存。把求出来的结果都缓存起来，就不用这么麻烦了。

五、主定理

主定理的作用是：任何一个递归函数的时间复杂度都可以用主定理来算出来

下面的这四种是一般面试中常见的四个主定理公式，大家记住这四种就可以了。

第一种：二分查找,把有序数列一分为二，每次只查一边。时间复杂度为O(logn)

第二种：二叉树的遍历。通过主定理的计算公式推算可以计算出来时间复杂度为O(n).简单的理解，我们会访问到二叉树的每一个节点且只会访问一次，所以事件复杂度是O(n)。

第三种：在一个排好序的二维矩阵中进行二分查找，通过主定理公司计算的话也是O(n).这个大家对比着一位数组二分查找，记住就好了。

第四种：归并排序。时间复杂度是O(nLogn) .这也是常用排序算法中时间复杂度最高的。

 

六、思考题

1、二叉树的遍历，中序、后序、前序的时间复杂度是多少？

答：都是O(n)。因为不管怎么遍历他的每一个节点都是访问仅访问 一次的。所以是线性变化。O(n)

2、图的遍历时间复杂度是多少？

答：也是O(n).n指的是图的里面的节点总数。因为图的遍历也是每一个节点仅访问一次。

3、搜索算法：DFS（深度优先）、BFS（广度优先）时间复杂度是 多少？

答：也是O(n)。n指的是搜索空间里面的节点总数。

 

空间复杂度分析

空间复杂度的分析就遵循两个原则

1、如果代码中开辟了数组，那么数组的长度基本上就是代码的空间复杂度。

例如开了一维数组，长度就是O()

2、如果代码中有递归的话，递归深度的最大值就是代码的空间复杂度。

具体的空间复杂度和时间复杂度的分析实例，我们可以去LeetCode上爬楼梯问题的官方题解的分析，可以有所了解

 

相关链接

爬楼梯问题：https://leetcode-cn.com/problems/climbing-stairs/solution/

时间复杂度理解：https://www.zhihu.com/question/21387264