2014 - ICPC - Beijing 补

把训练时没过的题补了一下

E - Everlasting L （HDU - 5116）
训练的时候因为没给数据组数，一直不敢写的做法其实是正解…

这题问的是有多少对不相交的优秀的L，优秀的L定义为竖的长度和横的长度互质
我们把L左下角那个点定义为关键点
考虑两个关键点的关系
手画一下其实就

1. 两个关键点y坐标相同
   
   2.两个关键点x坐标相同
   
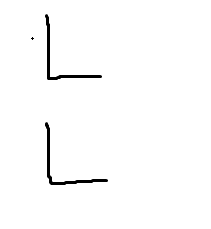
   3.A关键点在B关键点的左下方
   
   4.B关键点在A关键点的右下方，且B的x坐标<=A的L最右端
   
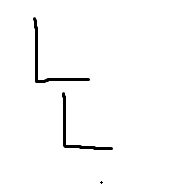
   5.B关键点在A关键点右下方，且B的x坐标>A的L最右端
   
   其中第1类可以并入第5类，第二类可以并入第4类，所以只需要考虑3,4,5类情况
   第3类可以枚举B关键点坐标，对左下方矩阵做个前缀和
   第4类情况我们需要求一个add[x][y]表示关键点横坐标为x，L上端坐标为y的所有L的个数，然后再对这个add做个前缀和，统计的时候枚举A关键点的坐标，再枚举A的L的右端，通过add的前缀和数组可以统计这类情况的个数
   第5类可以枚举A关键点的坐标和A的L的右端，直接用第3类中用到的前缀和数组统计
   其实这题就是考虑一下各种情况然后前缀和搞搞

code：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ll long long
#define pb push_back
#define SZ(X) (int)X.size()
using namespace std;

int gcd(const int a,const int b){
      return !a?b:gcd(b%a,a); }
const int maxn = 204;

int s[maxn][maxn];

int v[maxn][maxn],tr[maxn][maxn],tu[maxn][maxn];
ll ini[maxn][maxn],sum[maxn][maxn],add[maxn][maxn],sum2[maxn][maxn];
int n;

int main()
{
     
    //freopen("tmp.in","r",stdin);
    
    for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) 
    {
     
        s[i][j]=s[i][j-1];
        if(gcd(i,j)==1) s[i][j]++;
    }
    
    int Tcase; scanf("%d",&Tcase);
    for(int tcase=1;tcase<=Tcase;tcase++)
    {
     
        memset(sum,0,sizeof sum);
        memset(ini,0,sizeof ini);
        memset(add,0,sizeof add);
        memset(v,0,sizeof v);
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
     
            int x,y;scanf("%d%d",&x,&y);
            v[x][y]=1;
        }
        for(int i=maxn-1;i>=1;i--)
        {
     
            for(int j=maxn-1;j>=1;j--)
            {
     
                if(v[i][j]) tu[i][j]=tu[i][j+1],tr[i][j]=tr[i+1][j];
                else tu[i][j]=j-1,tr[i][j]=i-1;
            }
        }
        for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) if(v[i][j])
        {
     
            int r=tr[i][j]-i;
            for(int k=j+1;v[i][k];k++)
                ini[i][j]+=s[k-j][r],add[i][k]+=s[k-j][r];
            sum[i][j]=ini[i][j];
        }
        for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) sum[i][j]+=sum[i][j-1];
        for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) sum[i][j]+=sum[i-1][j];
        for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) sum2[i][j]=sum2[i][j-1]+add[i][j];
        
        ll ans=0;
        for(int i=1;i<maxn;i++) for(int j=1;j<maxn;j++) if(v[i][j])
        {
     
            ans+=sum[i-1][j-1]*ini[i][j];
            ll now=sum2[i][j-1];
            for(int k=i+1;v[k][j];k++)
            {
     
                ans+=(sum[maxn-1][j]-sum[k][j])*s[k-i][tu[i][j]-j];
                now+=sum2[k][j-1];
                ans+=now*s[k-i][tu[i][j]-j];
            }
        }
        printf("Case #%d: %lld\n",tcase,ans<<1);
    }
    
    return 0;
}

G - GRE Words Once More! （HDU - 5118）
这题给了一个DAG，标记了一些特殊点，边上有值，Q个询问，问你从1出发的所有路径中字典序第ki小的路径的长度，两个路径比较字典序的方法是一条边一条边的比较权值

一开始我想dp每个点往后走有多少条路，然后每个询问去逐边确定这条路径，复杂度大概是$O(mq)$的但是我想着说不定卡不掉，然后就被卡T了

注意到询问的ki<=1e8，所以我们可以把字典序第1~1e8的所有路径长度搜出来
我们用ans[i]表示第i小的路径长度
这里有个保证了复杂度的优化：因为从每个点x出发到达能到的特殊点的所有路径是已经确定了的，假设有k条，所以如果之前已经搜过了点x，我再搜x的时候就可以利用之前搜得的k条路径直接更新我的ans，具体来说，如果我第一次搜到x时我已经搜得了firvis[x]条路径，当前1走到x的路径长度为L，点x搜完后我总计搜得了sum条路径，那么x这个点出发的路径有sum-firvis[x]条，他们的长度分别是ans[firvis[x]+1~sum]-L，所以我之后再搜到x的时候可以直接用这些路径去更新ans数组，就不用搜下去，这样保证了每个点只会被搜到一次，保证了复杂度是$O(n+m+1e8）$的

code：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ll long long
#define mp make_pair
#define pb push_back
#define SZ(X) (int)X.size()
using namespace std;

const int maxn = 210000;
const int maxk  = 1e8;

int n,m,Q;
vector< pair<int,int> >V[maxn];

int v[maxn];
int ans[maxk+1];
int firvis[maxn],firl[maxn],f[maxn],now;
void dfs(const int x,const int L)
{
     
    if(firvis[x]!=-1)
    {
     
        for(int i=1;now<maxk&&i<=f[x];i++)
            ans[++now]=ans[firvis[x]+i]+L-firl[x];
        return;
    }
    firvis[x]=now;
    firl[x]=L;
    if(v[x]) ans[++now]=L;
    for(int i=0;i<SZ(V[x])&&now<maxk;i++) dfs(V[x][i].second,L+1);
    f[x]=now-firvis[x];
}

int main()
{
     
    //freopen("tmp.in","r",stdin);
    
    int Tcase; scanf("%d",&Tcase);
    for(int tcase=1;tcase<=Tcase;tcase++)
    {
         
        printf("Case #%d:\n",tcase);
        
        scanf("%d%d%d",&n,&m,&Q);
        for(int i=1;i<=n;i++) V[i].clear();
        for(int i=1;i<=n;i++) firvis[i]=-1,firl[i]=f[i]=0;
        
        for(int i=2;i<=n;i++) scanf("%d",&v[i]);
        for(int i=1;i<=m;i++)
        {
     
            int u,v,w;scanf("%d%d%d",&u,&v,&w);
            V[u].pb(mp(w,v));
        }
        
        for(int i=1;i<=n;i++) sort(V[i].begin(),V[i].end());
        now=0;
        dfs(1,0);
        
        for(int i=1;i<=Q;i++)
        {
     
            int k;scanf("%d",&k);
            if(k>now) puts("-1");
            else printf("%d\n",ans[k]);
        }
    }
    
    return 0;
}

J - Just A Mistake （HDU - 5121）
给一棵树点编号1~n
对于一个n的排列，按顺序将点加入集合S，如果一个点x能被加入当且仅当加入x时集合S里面没有x相邻的点
问n的全排列对应的集合S的大小之和

这题其实不是很难，想通了就挺好做的
当一个点x因为和集合S中的y相邻不能加入集合时，我们称x被y顶出了集合
肯定要dp，那要考虑的就是子树之间的合并，合并时会产生影响的只是这两棵子树的树根在排列中的先后关系

我们定义f[i][0/1/2][j]代表对于当前i的子树里点的所有排列，点i位于排列中第j个，集合S的大小之和，其中的0/1/2
0：i已经被排列里的点顶出集合；
1：i一定在集合里；
2：排列中i前面的点还没有能把i顶出集合的，但是i会被之后加入子树的点或者i的父亲顶出集合
再定义一个g数组，对上面每个状态记录有多少种排列满足这个状态
之所以要定义g数组是因为f和f之间不能直接合并，要通过g数组算两棵子树分别的贡献再合并起来

然后就dp一下，怎么转移懒得写了，大概就是排列合并一下，乘个组合数什么的，不是很难
复杂度$O(n^3)$

code：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define ll long long
using namespace std;

const int maxn = 210;
const int mod  = 1e9+7;
inline void add(int &a,const int &b){
      a+=b;if(a>=mod)a-=mod; }
inline void dec(int &a,const int &b){
      a-=b;if(a<0)a+=mod; }

int n;
int C[maxn][maxn];
struct edge
{
     
    int y,nex;
}a[maxn<<1]; int len,fir[maxn];
inline void ins(const int x,const int y){
      a[++len]=(edge){
     y,fir[x]};fir[x]=len; }

int siz[maxn];
int f[maxn][3][maxn],g[maxn][3][maxn],tempf[3][maxn],tempg[3][maxn];
void init(const int x)
{
     
    siz[x]=1;
    f[x][0][1]=g[x][0][1]=0;
    f[x][1][1]=g[x][1][1]=1;
    f[x][2][1]=0,g[x][2][1]=1;
}
void merge(const int x,const int y)
{
     
    int all=siz[x]+siz[y];
    for(int k=0;k<3;k++) for(int i=0;i<=all;i++) tempf[k][i]=tempg[k][i]=0;
    
    //0+0 0+1 1+0 2+0
    for(int c1=0;c1<3;c1++) for(int c2=0;c2<2;c2++) 
        if(c1+c2<=1||(c1==2&&c2==0))
        {
     
            for(int i=1;i<=siz[x];i++) for(int j=1;j<=siz[y];j++) for(int k=i;k<=i+siz[y];k++)
                add(tempf[c1][k],(ll)f[x][c1][i]*g[y][c2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
                add(tempf[c1][k],(ll)g[x][c1][i]*f[y][c2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
                add(tempg[c1][k],(ll)g[x][c1][i]*g[y][c2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod);
        }
    //1+2->1
    for(int i=1;i<=siz[x];i++) for(int j=1;j<=siz[y];j++) for(int k=i;k<=i+j-1;k++)
        add(tempf[1][k],(ll)f[x][1][i]*g[y][2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempf[1][k],(ll)g[x][1][i]*f[y][2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempg[1][k],(ll)g[x][1][i]*g[y][2][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod);
    //2+1->0
    for(int i=1;i<=siz[x];i++) for(int j=1;j<=siz[y];j++) for(int k=j+i;k<=siz[y]+i;k++)
        add(tempf[0][k],(ll)f[x][2][i]*g[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempf[0][k],(ll)g[x][2][i]*f[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempg[0][k],(ll)g[x][2][i]*g[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod);
    //2+1->2
    for(int i=1;i<=siz[x];i++) for(int j=1;j<=siz[y];j++) for(int k=i;k<=i+j-1;k++)
        add(tempf[2][k],(ll)f[x][2][i]*g[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempf[2][k],(ll)g[x][2][i]*f[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod),
        add(tempg[2][k],(ll)g[x][2][i]*g[y][1][j]%mod*C[k-1][i-1]%mod*C[all-k][siz[x]-i]%mod);
        
    for(int k=0;k<3;k++) for(int i=1;i<=all;i++)
        f[x][k][i]=tempf[k][i],g[x][k][i]=tempg[k][i];
    
    siz[x]+=siz[y];
}
void dp(const int x,const int fa)
{
     
    init(x);
    for(int k=fir[x],y=a[k].y;k;k=a[k].nex,y=a[k].y) if(y!=fa)
        dp(y,x),merge(x,y);
}

int main()
{
     
    //freopen("tmp.in","r",stdin);
    //freopen("tmp.out","w",stdout);
    
    C[0][0]=1;
    for(int i=1;i<maxn;i++)
    {
     
        C[i][0]=1;
        for(int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
    }
    
    int Tcase; scanf("%d",&Tcase);
    for(int tcase=1;tcase<=Tcase;tcase++)
    {
     
        scanf("%d",&n);
        len=0;for(int i=1;i<=n;i++) fir[i]=0;
        for(int i=1;i<n;i++)
        {
     
            int x,y; scanf("%d%d",&x,&y);
            ins(x,y),ins(y,x);
        }
        
        dp(1,0);
        int ans=0;
        for(int i=1;i<=n;i++) add(ans,f[1][0][i]),add(ans,f[1][1][i]);
        printf("Case #%d: %d\n",tcase,ans);
    }
    
    return 0;
}