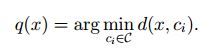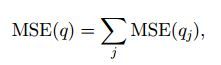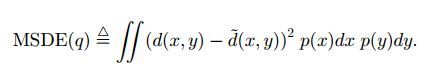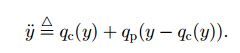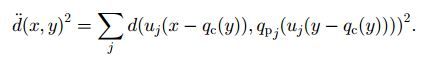图像检索之product quantization 算法解析

        图像搜索首先需要提取图像的特征信息。由于全局信息具有不稳定性和敏感性，鲁棒性较差。所以现在一般都提取图像的局部信息，如SIFT，SUFT等。这样，一副图像就可以用许多特征点组成。每个特征点用一个向量表示，对于SIFT，SUFT，这个向量是128维的。在提取出特征向量之后。因为一般每幅图像都可以提取几百上千个特征点，为了方便图像匹配，一般还需要将这些特征向量聚合成一个向量，方便比较。当然，也不是所有的算法都需要将特征向量进行聚合。

      

       因此可以看到图像匹配的本质就是比较向量的相似程度。现在主要是通过比较向量的欧式距离来比较他们的相似程度。比较过程就是对于一个输入向量，在数据库中找到与其在欧式空间上距离最近的向量。因此，朴素的算法是对数据库中的特征向量进行遍历。因为要找到最邻近的匹配值，起码都要把所有的向量比较一遍。但有两个问题，一个是数据库中一般含有的特征向量数目非常多，起码都是千万级别的。因此遍历一遍会花很多时间；其次，计算向量之间的欧氏距离也是一个花销非常大的过程。

      为了解决最邻近算法的这些问题，现在提出了近似最邻近算法(approximate nearest neighbor-ANN)。ANN算法目的不是寻找最邻近向量，而是近似最邻近向量。

     ANN算法的核心思想是先建立codebook,，然后将特征向量量化到code word上。最后通过比较对应的code word的距离即可。可以认为被量化到同一个code word上的特征是近似最邻近的。因此前面的距离算法到这里就编程了量化算法。但是量化算法也有一些缺点，就是存在量化误差-可能会把欧式空间中相邻的特征量化到不同的code word上。毕竟量化过程会丢失特征向量的某些特征。为了弥补这些误差，各种算法都提出了一些优化措施。

     本文主要是介绍量化算法中的一种叫做product quantization。目前有许多很有名的ANN算法，product quantization是其中比较好的算法。相关详细信息可以参考论文：Jegou, Herve, Matthijs Douze, and Cordelia Schmid. "Product quantization for nearest neighbor search." Pattern Analysis and Machine Intelligence, IEEE Transactions on 33.1 (2011): 117-128

      1.背景知识

     首先介绍一下向量量化的一些背景知识。向量量化的目标是为了减少空间结构的复杂度。因为经过量化，任何空间中的点都可以用有限的几个code word来表示。假设存在量化函数q，和词汇 C，则对于空间中的任何一个向量x都有

     

       其中i=1,2,...,k。即codebook中code word的数目。

      所以一个code word中所包含的特征向量集合(vi)可以用下式表示

                                                                         

       因此量化过程直观上的理解就是对特征空间进行分割。为了对量化进行评价，我们引入均方误差(Mean Squared Error)：

                                                        

       式中的p(X)表示X的分布函数。因此对于特定的x，p(x)表示X落在该点的概率。

       可以看到MSE(q)是通过计算空间中所有点到其量化点的距离的期望值对量化函数q进行评价。可以很直观地看出，对于所有的q，MSE(q)的值越小，说明此量化函数的量化误差越小，量化效果越好。

        既然量化函数是可以进行量化评价的，那么肯定就存在一个量化函数，对于一些特定的点可以训练得到最小的MSE。亦即存在最优的量化函数。下面利用Lloyd optimality conditions定义量化函数的最优化条件。

                                                                        

                                                                                    

            式一是对量化函数的描述，表示向量x一定要量化到离他最近的code word上面。

         式二是对code word的定义。可以看出这是一个需要反复修正的训练过程。

 

         可以把满足以上两个最优化条件的量化算法称为Lloyd 量化器。我们熟知的k-means算法就是一个Lloyd量化器。它是一个接近最优化的量化算法，难怪如此深入人心。

        为了后面的讨论，再定义均方失真函数

                                                                    

         式子中，pi(x)表示x被量化到ci上面的概率分布。

       

         2.Product Quantizer

            本节详细介绍product  quantization。

             product  quantization是一种常用的编码方法。它允许将一个向量的各个部分进行分开量化。

                                                                                                            

                    如图，将一个向量分成m等份进行分开量化。这样，每个量化函数都相对简单，因为它只需要处理维数比较少的子向量即可。算法还分别为每个子量化器分配了一个codebook，假设为量化器qi，分配的codebook是ci。则原向量最终的量化空间将是这些codebook的笛卡尔乘积

                                                                                 

              假设每个子量化器都有k*个code word，则对于原向量，可选的codeword一共有

                                                                                           

              product quantization的优势在于，通过对将较小的几个code book连接形成一个规模足够大的codebook。而且对于小的codebook，训练复杂度相对直接训练大的codebook是低的多的。所以根据这个原理，直接存储C个codebook是没必要的，且相反会降低最终的量化速率。因此在存储的时候，我们采用的是分别存储m个大小为k*的codebook的方式。

                   所以剩下的问题就是如何确定参数k* 和 m了。k*和m是通过MSE函数为指标确定的，MSE函数值越小越好。因为现在量化是分步进行，最后再将量化结果整合，因此需要重新定义MSE函数

                                                                       

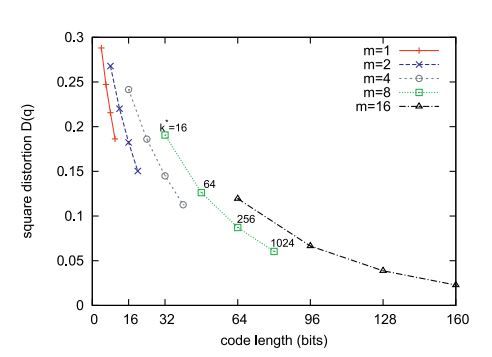
            下图是论文中描绘的MSE函数值与(k*,m)的函数关系图

                                              

             其中code length可由m,k*计算得到 :codelength = m*log2(k*)。

             通过图可以看出，对于一个 codelength，m越小，k*越大，则MSE的值会越小。比如当m=1时，算法就进化为满足最优化条件的k-means算法。只是由于k-means算法对高维复杂度比较高，因此不予以考虑。所以m和k*的选取是一个trade off的问题。

             3.利用product quantization进行检索

              正如前面说的一样，检索本质上是一个比较欧式距离的问题。因此现在主要看看如何通过量化后的code word 对向量进行efficient的比较。

                                        

              如图所示，计算待查询向量和数据库中的向量的距离有两种方法。一种是，先将待查询向量进行量化，然后计算对应的量化子和数据库中的量化子的距离(SDC)；另一种是不需要对待查询向量进行量化，而直接计算它和数据库中的量化子的距离(ADC)。两种方法可分别用下面两个式子说明

                                                     

                                                      

               可以看到SDC相对于ADC，只有一个优点，就是不需要在内存中存储query vector，因为它已经被量化到codeword上了，直接用这个code word表示它就可以，而code code本省是存在内存中的。所以下面只考虑ADC算法。

               但是需要注意的是，这里进行距离计算时还是需要遍历数据库中的m*(k*)个code book的。只是相对来说，这个值要小的多。下面着重分析一下ADC算法的距离误差。(PS：这个分析方法具有普遍性，并不是只适合于分析product  quantizer)

                 

               4.误差分析

               首先定义平均距离方差指标(Mean Squared Distance Error) - MSDE

                                                     

               根据三角不等式

                                                  

                于是有

                                                                 

                因此由MSDE函数定义可得到下面的不等式

                                                      

              式中的MSE(q)是前面已定义的。

              由以上不等式表明，我们的量化方法误差上界是MSE(q)，而我们的quantizer是用k-means算法进行学习的，因此可以保证MSE(q)满足进行虽有条件。这样，我们的最终算法的误差控制是比较好的。

             但是不管怎么样，用量化值进行距离计算总是免不了偏差的。如下图，分别比较了实际的距离和ADC,SDC的距离之间的函数关系

                                           

      可以看到整体来说，量化距离和实际距离是呈正相关关系的，但是误差也是不可避免的。同时也可以看到，量化距离一般比实际距离的值要偏小一些，并且SDC算法的偏差相对ADC的偏差更大。原论文对偏差做了一定的修正。在这里就不赘述了。因为在实际应用中，可以不进行校正。不过从上图也可以看出用ADC算法会更加好一些。下面我们直接看一下检索过程。

                                         

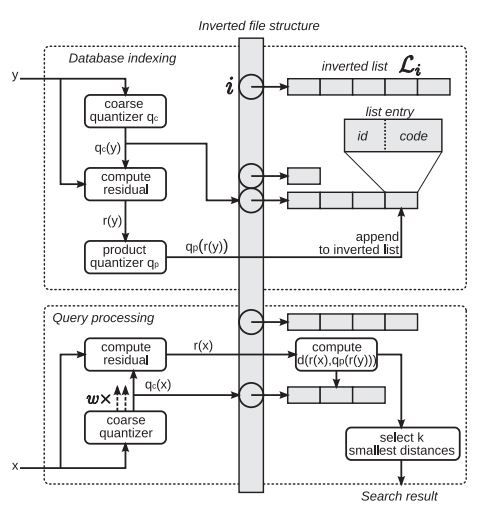
为了快速检索，不例外地这里用到了倒排索引结构(inverted index)。上图可以进行说明，在实际检索中分两个步骤

                         1.用数据库中特征建立索引结构(图的上部分)

 2.对输入的待检测特征进行检索(图的下部分)

        从图中可以看到。在建立索引时，先用k-means算法对数据库特征进行粗量化，得到K'个索引项；粗量化之后，由于会存在较大的量化误差。为了保存这个信息，这里计算query vector和粗量化的code word之间的residual vecto-r。这里的residual vector就是将使用本文所讲的product quantization 算法进行量化，最后将量化后得到的quantiza-tion code 存储在该索引项对应的列表项中，同时列表项中还存储中图片的identifier。这样一个向量y就可以用下面的向量近似：

                                                                   

         因此d(x,y)可以用下面的近似算法进行计算：

                                                     

         将计算任务分配到product quantization的各个subquantizers中可得到下式

                                                   

          需要注意的是，x项是粗量化的code word，因此是precomputed，因此该式子第一部分是可以离线计算的。

不过这里得存储粗量化所有的code word的sub vector到所有的product quantization的code word 的距离，也是非常耗内存的。为了减少量化误差，论文中还应用了multiple assignment的方法，就是将一个特征映射到多个索引上。

         

           以上就是product quantization的一些基本思想。具体的算法流程可以查阅相关论文。