第二周任务：主层次分析法（原理，代码，实例）
引言：在许多实际问题中，多个变量之间是具有一定的相关关系的。因此，我们就会很自然地想到，能否在各个变量之间相关关系研究的基础上，用较少的新变量代替原来较多的变量，而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信息？事实上，这种想法是可以实现的，这里介绍的主成分分析方法就是综合处理这种问题的一种强有力的方法。
1.主成分分析法步骤：
-
对原始数据进行标准化处理。
-
计算样本相关系数矩阵。
-
计算相关系数矩阵R的特征值和相应的特征向量。
-
选择重要的主成分，写出主成分表达式。
-
相应的代码（以实例说明）：
%主成分分析 PAC 的Matlab实现
%------------------------
% % 数据的输入及处理
clc
clear all
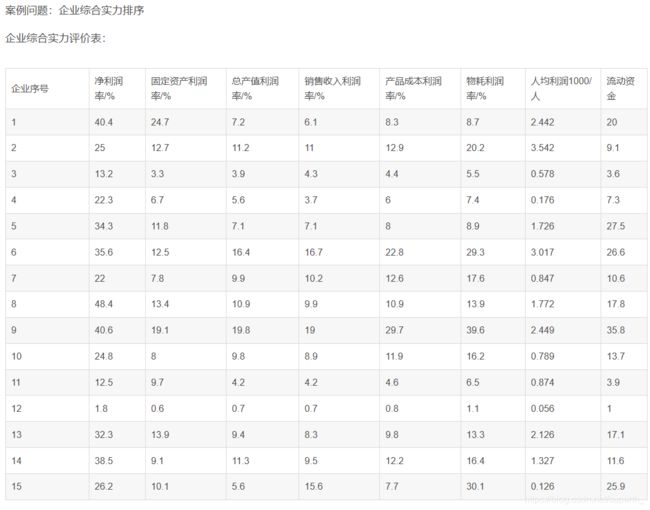
A=xlsread('D:\evaluation.xlsx',1,'B2:I16');
%数据的标准化处理
a=size(A,1);%获得矩阵A的行大小
b=size(A,2);%获得矩阵A的列大小
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));%std函数是用来求向量的标准差
end
% %计算相关系数矩阵的特征值和特征向量
CM=corrcoef(SA);%计算相关系数矩阵
[V,D]=eig(CM);%计算特征值和特征向量
for j=1:b
DS(j,1)=D(b+1-j,b+1-j);%对特征值按降序排列
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));%贡献率
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率
end
% % 选择主成分及对应的特征向量
T=0.9;%主成分信息保留率
for k=1:b
if DS(k,3)>=T
Com_num=k;
break;
end
end
%提取主成分对应的特征向量
for j=1:Com_num
PV(:,j)=V(:,b+1-j);
end
% % 计算各评价对象的主成分得分
new_score=SA*PV;
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
result_report=[new_score,total_score];%将各主成分得分与总分放在同一个矩阵中
result_report=sortrows(result_report,-4);%按总分降序排序
% % 输出模型及结果报告
disp('特征值及其贡献率，累加贡献率：')
DS
disp('信息保留率T对应的主成分数与特征向量：')
Com_num
PV
disp('主成分得分及排序（按第四列的总分进行排序，前三列为个主成分得分，第五列为企业编号）')
result_score
特征值及其贡献率，累加贡献率：
DS =
5.7361 0.7170 0.7170
1.0972 0.1372 0.8542
0.5896 0.0737 0.9279
0.2858 0.0357 0.9636
0.1456 0.0182 0.9818
0.1369 0.0171 0.9989
0.0060 0.0007 0.9997
0.0027 0.0003 1.0000
信息保留率T对应的主成分数与特征向量：
Com_num =
3
PV =
0.3334 0.3788 0.3115
0.3063 0.5562 0.1871
0.3900 -0.1148 -0.3182
0.3780 -0.3508 0.0888
0.3853 -0.2254 -0.2715
0.3616 -0.4337 0.0696
0.3026 0.4147 -0.6189
0.3596 -0.0031 0.5452
主成分得分及排序（按第四列的总分进行排序，前三列为个主成分得分，第五列为企业编号）
result_report =
5.1936 -0.9793 0.0207 4.2350 9.0000
0.7662 2.6618 0.5437 3.9717 1.0000
1.0203 0.9392 0.4081 2.3677 8.0000
3.3891 -0.6612 -0.7569 1.9710 6.0000
0.0553 0.9176 0.8255 1.7984 5.0000
0.3735 0.8378 -0.1081 1.1033 13.0000
0.4709 -1.5064 1.7882 0.7527 15.0000
0.3471 -0.0592 -0.1197 0.1682 14.0000
0.9709 0.4364 -1.6996 -0.2923 2.0000
-0.3372 -0.6891 0.0188 -1.0075 10.0000
-0.3262 -0.9407 -0.2569 -1.5238 7.0000
-2.2020 -0.1181 0.2656 -2.0545 4.0000
-2.4132 0.2140 -0.3145 -2.5137 11.0000
-2.8818 -0.4350 -0.3267 -3.6435 3.0000
-4.4264 -0.6180 -0.2884 -5.3327 12.0000
相应的方法在代码里都能找到。
3.主成分分析函数：
[coeff,score,letent]=princomp(x);
x：为要输入的n维原始数据。带入这个matlab自带函数，将会生成新的n维加工后的数据（即score）。此数据与之前的n维原始数据一一对应。
score：生成的n维加工后的数据存在score里。它是对原始数据进行的解析，进而在新的坐标系下获得的数据。他将这n维数据按供献率由大到小分列。（即在改变坐标系的景象下，又对n维数据排序）
latent：是一维列向量，每一个数据是对应score里响应维的供献率，因为数占领n维所以列向量有n个数据。由大到小分列（因为score也是按供献率由大到小分列）。
coef：是系数矩阵。经由过程cofe可以知道x是如何转换成score的。但这个转换不是单纯的转换，必须使用下列计算方法，即score（：，i）=coef*（x（：，i）-mean（x（：，i））），这样才能得到。
用你的原矩阵x*coeff(:,1:n)才是你要的的新数据，其中的n是你想降到多少维。而n的取值取决于对特征值的累计贡献率的计算。
参考：https://blog.csdn.net/sungaochao/article/details/46959607