POJ 1920 :Towers of Hanoi
Towers of Hanoi
| Time Limit: 3000MS | Memory Limit: 16000K | |
| Total Submissions: 2239 | Accepted: 999 | |
| Case Time Limit: 1000MS | ||
Description
Surely you have already come across the Towers of Hanoi problem: Wooden disks of different sizes are stacked on three pegs, and initially, all disks are stacked on the same peg sorted by size, with the largest disk at the bottom. The objective is to transfer the entire tower to one of the other pegs, moving only one disk at a time and never putting a larger disk onto a smaller one.
According to an old myth, the monks at an ancient Tibetian monastery have been trying to solve an especially large instance of this problem with 47 disks for thousands of years. Since this requires at least 2 47 - 1 moves and the monks started out without a strategy, they messed it all up while still following the rules. Now they would like to have the disks stacked up neatly on any arbitrary peg using the minimum number of moves. But they all took a vow which forbids them to move the disks contrary to the rules. They want to know on which peg they should best stack the disks, and the minimum number of moves needed.
Write a program that solves this problem for the monks. Your program should also be able to handle any number N (0 < N <= 100 000) of disks. The numbers involved in the computation can become quite large. Because of that, the monks are only interested in the number of moves modulo 1 000 000.
Example
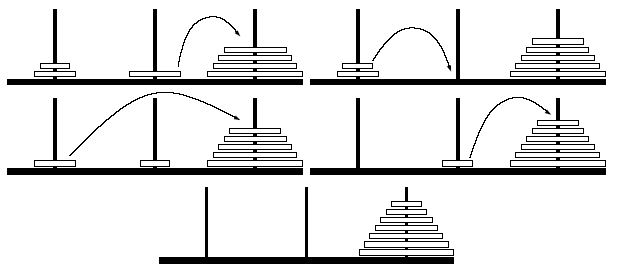
The following example can be solved in four moves.
According to an old myth, the monks at an ancient Tibetian monastery have been trying to solve an especially large instance of this problem with 47 disks for thousands of years. Since this requires at least 2 47 - 1 moves and the monks started out without a strategy, they messed it all up while still following the rules. Now they would like to have the disks stacked up neatly on any arbitrary peg using the minimum number of moves. But they all took a vow which forbids them to move the disks contrary to the rules. They want to know on which peg they should best stack the disks, and the minimum number of moves needed.
Write a program that solves this problem for the monks. Your program should also be able to handle any number N (0 < N <= 100 000) of disks. The numbers involved in the computation can become quite large. Because of that, the monks are only interested in the number of moves modulo 1 000 000.
Example
The following example can be solved in four moves.

Input
The first line of the input file hanoi.in consists of the number N (N <= 100000) of disks. The second line consists of three integers s1, s2, s3 with 0 <= s1, s2, s3 <= N and s1+s2+s3 = N, the number of disks on each of the three pegs. Lines three to five each contain the sizes of the disks for one peg. More precisely:
The (i + 2)-th line of the input file consists of integer numbers m i,1 . . .m i,si with 1 <= m i,j <= N, the sizes of the disks on peg i. The disks are given from bottom to top, thus m i,1 > m i,2 > . . . > m i,si .
Note that an empty stack is given by an empty line. The set of N disks have different sizes. All numbers are separated by a single space.
The (i + 2)-th line of the input file consists of integer numbers m i,1 . . .m i,si with 1 <= m i,j <= N, the sizes of the disks on peg i. The disks are given from bottom to top, thus m i,1 > m i,2 > . . . > m i,si .
Note that an empty stack is given by an empty line. The set of N disks have different sizes. All numbers are separated by a single space.
Output
The first line of the output file hanoi.out consists of the number d in {1, 2, 3} of the peg onto which the disks can be stacked using the minimum number of moves. The second line consists of the number M of required moves modulo 1 000 000.
Sample Input
7 2 1 4 2 1 3 7 6 5 4
Sample Output
3 4
这个汉诺塔与之前的Hackerrank那道题是有着相当相当大的不同,一开始为了解决Hakerrank那道题特意做了一下这道题,然后用这个3个柱子的思路去往4个柱子的思路上面套。
总体思路是一致的,都是倒过来想,看最原始的状态如何能够到达目标状态。
当时问题在于3个柱子的拿出来的时候状态是固定的,即其他比这个小的一定摞在另一个柱子上,而四维的情况下,你是没有办法判断这个状态的。所以那道题n最多是10,让你自己去枚举状态。
这个题就是从最大的那个盘子开始到目标的盘子,然后其余比这个小的盘子一定在3个柱子的另外一个空柱子上面,然后这个柱子就作为下一次的起始柱子了。
代码:
#pragma warning(disable:4996)
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include