leetcode_887_鸡蛋掉落

参考链接1：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/gao-lou-reng-ji-dan-wen-ti

参考链接2：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/gao-lou-reng-ji-dan-jin-jie

参考链接3：https://leetcode-cn.com/problems/super-egg-drop/solution/zhi-xing-yong-shi-0-ms-zai-suo-you-java-ti-jia-121/

解法一：递归版    动态规划+备忘录+二分优化

函数dp(K,N)表示此时有K个鸡蛋，楼层有N层需要测试多少次。

base case:

K==1时，即手中只有一个鸡蛋，需要测试N次

N==0时，即处于0层，需要测试0次

在第i层楼扔了鸡蛋之后会出现鸡蛋碎了和鸡蛋没碎两种情况。

如果鸡蛋碎了，那么鸡蛋的个数 K 应该减一，搜索的楼层区间应该从 [1..N] 变为 [1..i-1] 共 i-1 层楼；

如果鸡蛋没碎，那么鸡蛋的个数 K 不变，搜索的楼层区间应该从 [1..N] 变为 [i+1..N] 共 N-i 层楼。

因为我们要求的是最坏情况下扔鸡蛋的次数，所以鸡蛋在第 i 层楼碎没碎，取决于那种情况的结果更大：

所以下面求res（最坏情况下的最少扔鸡蛋次数）时，因该先对dp(K-1,i-1)和dp(K,N-i)求一下最大值然后加1再与res比较求最小值。

 

二分优化是因为：

dp(K-1,i-1)单调递增，dp(K,N-i)单调递减（具体为什么看参考链接1，作者写得很清楚），利用二分求这俩函数的交点

下面代码中，带注释的是没用二分优化求res的代码，也能通过。二分优化的代码没注释掉。

class Solution:
    def superEggDrop(self, K: int, N: int) -> int:
        memo=dict()
        def dp(K,N)->int :
            if(K==1):return N
            if(N==0):return 0

            if(K,N) in memo:
                return memo[(K,N)]
            res=float('INF')
            #for i in range(1,N+1):
             #   res=min(res,
              #  max(dp(K-1,i-1),dp(K,N-i))+1
               # )
            ###二分优化，见labuladong
            l,r=1,N
            while(l<=r):
                mid=(r+l)//2
                broken=dp(K-1,mid-1)
                notbroken=dp(K,N-mid)
                if(notbroken>broken):
                    l=mid+1
                    res=min(res,notbroken+1)
                else:
                    r=mid-1
                    res=min(res,broken+1)

            memo[(K,N)]=res

            return res
        return dp(K,N)

解法二：非递归版动态规划

修改 dp 数组的定义，确定当前的鸡蛋个数和最多允许的扔鸡蛋次数(m)，就知道能够确定 F 的最高楼层数（参考链接2)

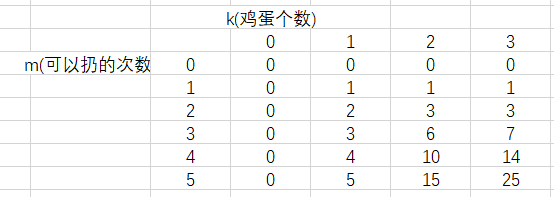
dp[k][m] = n
# 当前有 k 个鸡蛋，可以尝试扔 m 次鸡蛋
# 这个状态下，最坏情况下最多能确切测试一栋 n 层的楼

# 比如说 dp[1][7] = 7 表示：
# 现在有 1 个鸡蛋，允许你扔 7 次;
# 这个状态下最多给你 7 层楼，
# 使得你可以确定楼层 F 使得鸡蛋恰好摔不碎
# （一层一层线性探查嘛）

我们最终要求的其实是扔鸡蛋次数 m，但是这时候 m 在状态之中而不是 dp 数组的结果，可以这样处理：

int superEggDrop(int K, int N) {

    int m = 0;
    while (dp[K][m] < N) {
        m++;
        // 状态转移...
    }
    return m;
}

1、无论你在哪层楼扔鸡蛋，鸡蛋只可能摔碎或者没摔碎，碎了的话就测楼下，没碎的话就测楼上。

2、无论你上楼还是下楼，总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1（当前这层楼）。

根据这个特点，可以写出下面的状态转移方程：

dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1

dp[k][m - 1] 就是楼上的楼层数，因为鸡蛋个数 k 不变，也就是鸡蛋没碎，扔鸡蛋次数 m 减一；

dp[k - 1][m - 1] 就是楼下的楼层数，因为鸡蛋个数 k 减一，也就是鸡蛋碎了，同时扔鸡蛋次数 m 减一。

 

优化二维的解法就是利用一维，将dp改成一维，这是因为二维dp更新时每次用到了上方元素和左上方元素，所以更新一维时要从后往前更新，这样上方和左上方的元素才没有被更改过。（参考链接3）

下面代码中被注释的是二维解法

class Solution {
    public int superEggDrop(int K, int N) {
        //int [][]dp=new int[K+1][N+1];

        int []dp=new int [K+1];

        int ans=0;
        while(dp[K]=1;i--)//一维数组反向遍历
                dp[i]=dp[i]+dp[i-1]+1;
        }
        return ans;

        /*int m=0;//二维数组正向遍历
        while(dp[K][m]