【数据结构知识】串（主要是KMP算法讲解）【一看就懂】

前言

        这一节主要针对字符串的包含算法KMP做详细介绍，关于求next数组有一点在这里要事先说明一下，就是关于需要匹配串的下标问题，在很多书本里面都是以1开始的，在这里为了和程序中下标一致，都是从0开始算起的，所以可能求出来的最后结果与你在其他地方看到的结果有冲突，开头看到这句话，可能还没理解。没关系，当你看完整篇博客，发现有疑问时，可以回过来看这句话。在写这篇博客之前，我也看过其他人写的关于这个算法，但都不是特别理解，在看完书本上介绍这个算法后，一步步手动计算，终于算是明白了，在此写下特别详细版，希望可以帮助大家理解KMP。

        最后，如果有写的不对的地方，希望大家不吝赐教，谢谢！

【数据结构系列】【前一章：栈和队列】【后一章：树】

四、串

串是由0个或多个字符组成的有限序列，也叫字符串。

存储结构：顺序存储和链式存储。

1、KMP模式匹配算法

例如有两个字符串：S=abcdefg，T=abcdex，对T和S进行匹配。

原始做法：

                                                                                        图1 原始匹配法 

如图1所示，两个字符串分别从头开始遍历，依次匹配，若匹配成功，则都向后移一位，进行下一次匹配，当不匹配时，则S串回溯到原始起点的下一个，而T串则回溯到开头的位置，重新进行第二轮匹配。。。这样重复下去，当T串遍历到末尾时，即匹配成功，否则在S串已经遍历到末尾，而T串未到末尾，则匹配失败。

这个方法很容易理解，但你会发现有很多重复的地方，比如在第一轮匹配时，T串的前5个字符都与S串的前5个字符匹配成功，即S[0-4]=T[0-4]，对于T串的第一个字符不与T串后面四个字符任何一个相等，即S[0]!=S[1-4]，由S[0-4]=T[0-4]推出S[1-4]=T[1-4]，所以S[0]!=T[1-4]，所以T串可以跳过从S串第二轮到第五轮的匹配，直接i从i=5开始，即第一轮断掉的地方开始。

博主注：为了方便理解，以S[0-4]代表S字符串的前五个字符，T[0-4]同样的道理，而S[0]!=S[1-4]即表示S串的第一个字符与后面的四个字符都不相等

我们会发现，这样匹配即用到了前一次匹配的信息，这里有个条件即是当前字符与后面已匹配的字符都不想等，这是非常重要的条件。那当有相等的情况又该如何处理呢？

例如：S=abcabcd，T=abcabx

第一轮匹配：当i=0、1、2、3、4，j=0、1、2、3、4时匹配成功，当i=5和j=5匹配失败，有S[0-5]=T[0-5]，但同时也有

T[0-1]=T[3-4]，即也有T[0-1]=S[3-4]所以进行第二轮匹配时，T串可以跳过对T[0-1]的匹配，j可以从j=2开始，同样i就从i=5开始。

第二轮匹配：i从i=5开始与j=2进行匹配

...

这就是KMP匹配法：i不断向前，j也是一直回溯，只是回溯的步数不是每次都回溯到开头了。关于回溯的具体位置，用next[j]来表示，我们要首先引用一个概念即前缀和后缀。

字符串：abcde

前缀：a,ab,abc,abcd

后缀：e,de,cde,bcde

对于T串abcabx来讲有前缀：a,ab,abc,abca,abcab，后缀：x,bx,abx,cabx,bcabx，所以：

                                                                            图2 next[j]计算方法

next[j]即与当前j位置的前面字符串中最长相等的前后缀长度相等。

再举几个例子计算一下：

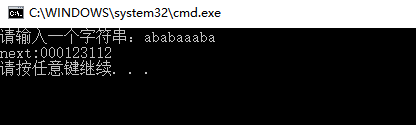
j           012345678

T         ababaaaba

next[j]  000123112

j          0123456789

T         aaaaaaaab

next[j] 001234567

 前面介绍了那么多，现在开始来写得到next数组的程序：

以串ababaaaba为例讲解规律，以i代表后缀元素下标，以j代表前缀下标：

a  b  a  b  a  a  a  b  a

0  1   2  3  4  5  6  7  8

初始化：next[0]=0,next[1]=0                                                                           规律：

i=1   j=0   s[0]!=s[1]  next[2]=0                                                                         1、当相等时：i++，j++

i=2   j=1   s[1]!=s[2]   j=next[1]=0   s[0]=s[2]  next[3]=1                                    2、当不等时：i不变，j回溯，j=next[j]

i=3   j=1   s[1]=s[3]  next[4]=2                                                                           3、除了i=1时，不等情况发生，而j没有回溯，

i=4   j=2   s[2]=s[4]  next[5]=3                                                                                 因为此时j=0，所以next[2]=0，其他情况

i=5   j=3   s[3]!=s[5]   j=next[3]=1  s[1]!=s[5]   j=next[1]=0   s[0]=s[5]   next[6]=1    都是next[i+1]=j+1

i=6   j=1   s[1]!=s[6]   j=next[1]=0  next[7]=2

i=7   j=1   s[1]=s[7]  next[8]=2

最后结果：000123112

 程序：

vector get_next(string s, vector next)
{
	int i = 1;
	int j = 0;
	next.push_back(0);
	next.push_back(0);
	while (i < s.length()-1)
	{
		if (s[i] == s[j]) //相等则i++,j++,同时next=j+1
		{
			next.push_back(++j);
			++i;
		}
		else
		{
			if (i == 1)  //若s[0]!=s[1]，则next[2]=0
			{
				next.push_back(j++);
				i++;
			}	
			else  //当不等时，j需要回溯到next[j]
				j = next[j];
		}
	}
	return next;
}

结果：

                                                                                   图3  next结果 

接下来开始写KMP算法，和原始算法不同的地方就是当j需要回溯时，是根据next[j]的值进行回溯，程序如下：

int KMP(string s1,string s2)
{
	vector next;
	next = get_next(s2, next);
	int i, j;

	for (i = 0, j = 0; i < s1.length(), j < next.size();)
	{
		if (s1[i] == s2[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
			i++;
		}
	}
	
	if (j ==next.size())
		return (i - next.size());
	else
		return 0;
}

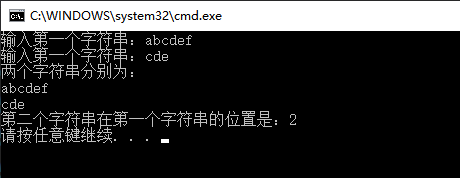
结果：

                                                                                 图4   KMP算法的结果 

到这里，貌似都很顺利，但后来发现还有点缺陷，就是当S=aaaabcde，T=aaaaad时，next=001234，当i从0开始遍历，j从0开始遍历，当遍历到4时，发现不匹配，如是回溯，根据next数组值，回溯到j=3，会发现还是不匹配，这样一直下去，最终j还是要回溯到0重新开始遍历，其实当T[4]!=S[4]时，由于T[0-3]=T[4]，所以很容易知道这样继续回溯回去都将是不匹配，那这样就相当于重复了好多步骤，我们需要对next数组进行修改下，来解决这个问题，即当此后缀与比较的前缀相等时，即把前缀的next值作为后缀的next值。

程序如下，做了改变地方已经标出：

vector get_next(string s, vector next)
{
	int i = 1;
	int j = 0;
	next.push_back(0);
	next.push_back(0);
	while (i < s.length()-1)
	{
		if (s[i] == s[j]) //相等则i++,j++,同时next=j+1
		{
			++j;
			++i;
			//下面是做了改变的地方
			if (s[i] != s[j])
				next.push_back(j);
			else
				next.push_back(next[j]); //若与前缀字符相同，则赋予前缀字符的回溯值
		}
		else
		{
			if (i == 1)  //若s[0]!=s[1]，则next[2]=0
			{
				next.push_back(j++);
				i++;
			}	
			else  //当不等时，j需要回溯到next[j]
				j = next[j];
		}
	}
	return next;
}

结果：

                                                                                    图5 改造后的next 

以上即是字符串的主要内容，关于字符串的应用还有很多。