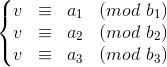中国剩余定理与扩展模板
中国剩余定理:
解决模数互质的线性同余方程组:
中国剩余定理给出了这类方程的解法:
(1)先求 X1 使得 X1 整除5、7 并且 X1%3==2,再求 X2 使得 X2 整除3、7并且 X2%5==3,最后求 X3 使得 X3 整除3、5 并且 X3%7==2
(2)那么 X = X1 + X2 + X3 必然是上述同余方程组的一个解,验证第一个方程:X2%3==0,X3%3==0,X%3==X1%3==2(符合题意)
(3)求X1:X1整除5、7,设X1 = 35y,则有 35y = 2 (mod 3),由于gcd(35,3)==1;那么利用扩展欧几里得容易解出方程:35yy = 1 (mod 3) 的解yy,即 35*yy%3==1,但此方程的余数为1,不难发现35*yy*2%3==2,所以 X1= 35*yy*2;在模数互质的情况下,利用扩展欧几里得算法就可解得X1、X2、X3.....
(4)X + k*lcm(3,5,7) 必然为上述同余式的通解,那么最小正整数解为:X%lcm
模板:
///要求模数两两互质
void Ex_gcd(int a,int b,int &x,int &y) //扩欧
{
if(b==0){x = 1;y = 0;return ;}
Ex_gcd(b,a%b,x,y);
int t = x;
x = y;
y = t - a/b*y;
}
int Crt()
{
int a,b,x,y,res=0,M=1;
for(int i=1;i<=n;++i) M = M*mod[i];
for(int i=1;i<=n;++i)
{
int a = M/mod[i]; //相当于上文中的35
int b = mod[i];
Ex_gcd(a,b,x,y);
x = (x%b+b)%b; //yy的最小正整数解
x = x*a*r[i]; //一组方程的解
res = (x+res)%M;
}
return res == 0 ? M : res;
}
扩展中国剩余定理:
解决线性同余方程组(不讨论模数)
不难得出:
![]()
![]()
![]()
同样利用欧几里得算法求解上式的 x,那么前两个同余方程组的解 v1 = b1x + a1;通解为:v = k*lcm(b1,b2) + v1
又可以得到一个同余方程:
![]()
那么前两个方程合并成了一个方程,依次这样合并下去,得到最终解
模板:
int Ex_gcd(int a,int b,int &x,int &y)
{
if(b==0){x=1;y=0;return a;}
int d = Ex_gcd(b,a%b,x,y);
int t = x;
x = y;
y = t - a/b*y;
return d;
}
int Ex_Crt()
{
int aa = b[1],rr=a[1],x,y;
for(int i=2;i<=n;++i)
{
int bb = b[i];
int c = a[i]-rr;
int d = Ex_gcd(aa,bb,x,y);
if(c%d) return -1; //c不能整除d,不存在整数解
c = c/d; bb = bb/d;
x = (x*c%bb+bb)%bb;
int lcm = aa*bb;
rr = (x*aa%lcm+rr)%lcm;
aa = lcm ;
}
return rr==0? aa:rr;
}应用
(1)洛谷3868(模板+快速乘)
///数据大了,先乘再取模,乘法就容易溢出,当然__int128可以避免
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e3+55;
ll aa[MAXN];
ll m[MAXN];
int n;
ll qmul(ll a,ll b,ll mod) //快速乘
{
ll ans = 0;
while(b>0)
{
if(b&1) ans=(ans+a)%mod;
a = (a+a)%mod;
b>>=1;
}
return ans;
}
void Ex_gcd(ll a,ll b,ll &x,ll &y)
{
if(b==0){x = 1;y = 0;return ;}
Ex_gcd(b,a%b,x,y);
ll tep = x;
x = y;
y = tep-a/b*y;
}
ll Crt()
{
ll M = 1,res = 0;
ll x,y;
for(int i=1;i<=n;++i) M = M*m[i];
for(int i=1;i<=n;++i)
{
ll tp = M/m[i];
Ex_gcd(tp,m[i],x,y);
x = (x%m[i]+m[i])%m[i];
res = (res+qmul(qmul(tp,x,M),aa[i],M))%M;
}
return res==0? M:res;
}
int main()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>aa[i];
for(int i=1;i<=n;++i) cin>>m[i];
for(int i=1;i<=n;++i) aa[i]=(aa[i]%m[i]+m[i])%m[i];//余数不能比模数大
cout< (2) 洛谷 4777(模板+_int128)
#include
#include
typedef __int128 ll;
const int MAXN = 1e5+55;
ll m[MAXN],r[MAXN];
int n;
inline ll read()
{
ll x=0,f=1;
char c = getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c = getchar();}
while(c>='0'&&c<='9'){x = c-'0'+x*10;c = getchar();}
return x*f;
}
inline void write(ll x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
ll Ex_gcd(ll a,ll b,ll &x,ll &y)
{
if(b==0){x=1;y=0;return a;}
ll d = Ex_gcd(b,a%b,x,y);
ll t = x;
x = y;
y = t - a/b*y;
return d;
}
ll Ex_Crt()
{
ll a = m[1],rr=r[1],x,y;
for(int i=2;i<=n;++i)
{
ll b = m[i];
ll c = r[i]-rr;
ll d = Ex_gcd(a,b,x,y);
c = c/d; b = b/d;
x = (x*c%b+b)%b;
ll lcm = a*b;
rr = (x*a%lcm+rr)%lcm;
a = lcm ;
}
return rr==0? a:rr;
}
int main()
{
n = read();
for(int i=1;i<=n;++i)
{
m[i] = read();
r[i] = read();
}
write(Ex_Crt());
return 0;
} (3)POJ 1006
(4)POJ 2891