最短路径Dijkstra算法原理通俗详解及Matlab代码分析
一、Dijkstra算法：两个指定顶点之间的短路径
不同点之间的邻接矩阵，为无向图，a(i，j) 表示从i点到j点的距离，两点不相通则用无穷表示，具体示例如下表所示
算法原理按照本人理解是将n个节点之间的查找（复杂度
）转化为两个n个节点的集合（查找集合和未查找集合）之间的查找（复杂度
），具体过程：从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
再具体一点如下图（与程序案例不同），查找节点1到节点6的所有最短路线
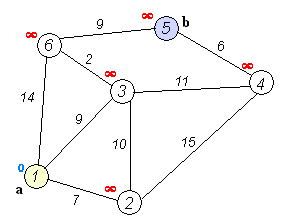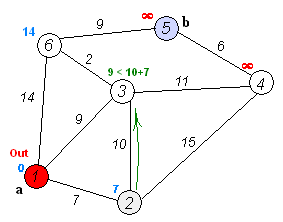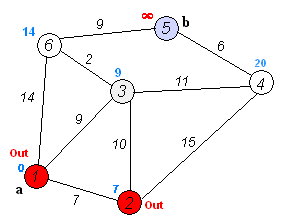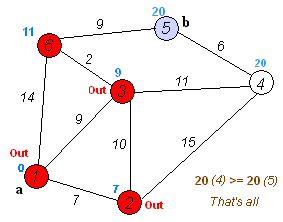
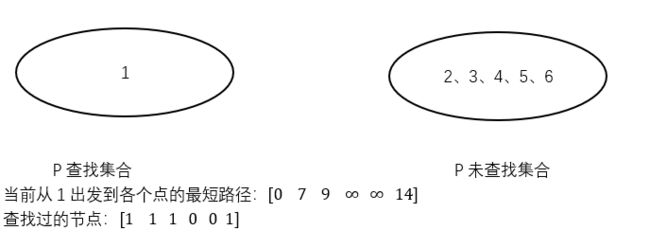
1.从节点1开始查找，将节点1放入查找集合P，剩余的节点2、3、4、5、6放入未查找集合W
2.寻找未查找集合W中与集合P相邻的集合中离节点1最近的节点（从上图能看到节点2、3、4、5、6对应的距离为7、9、
、、14中7最小，加入节点2，更新节点3、4），将最近节点2加入P，并将节点1到各个节点的距离更新，这里更新与2相连的节点3、4的最短距离：
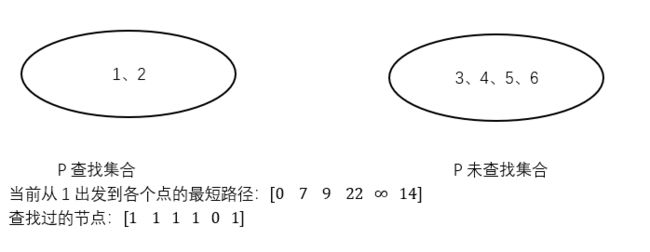
由于节点3：1→2的最短距离为7。从节点2出发，2→3的最短距离为10。因此节点1到3的最短路径为新老两种路径对比
1→2→3：原最短距离，1→3：9；步骤2产生新路径最短距离7+10=17；因此取最小值为9
由于节点4：1→2的最短距离为7。从节点2出发，2→4的最短距离为15。因此节点1到4的最短路径为新老两种路径对比
1→2→3：原最短距离，1→4：；步骤2产生新路径最短距离7+15=22；因此取最小值为22
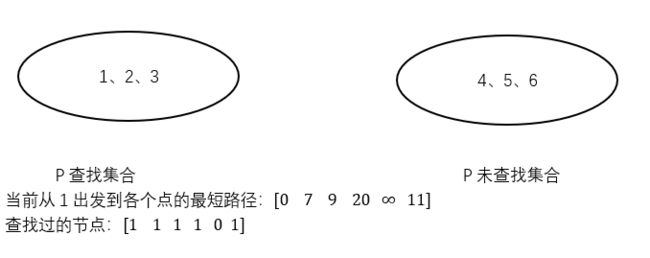
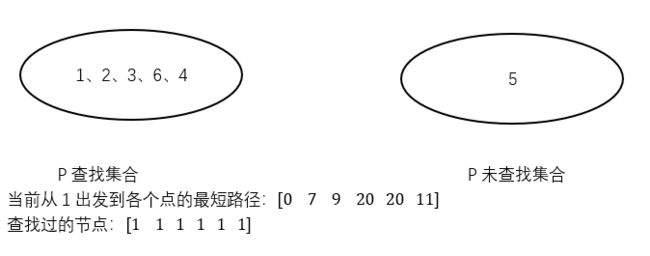
3.重复步骤2直到结束（从上图中能看到节点3、4、5、6对应的距离为9、22、、14中9最小，加入节点3，更新4和6）
（从上图中能看到20、、14中14最小，加入节点6，更新5）
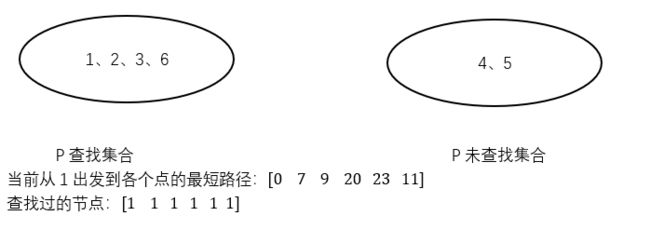
（从上图中能看到20、23中20最小，加入节点4，更新5）
最后加入5，此时未查找集合元素为0，结束！
二、Matlab代码及解析
主函数：
主函数构建邻接矩阵，首先从节点1开始找到其与2、3、4、5、6的距离，然后找到节点2到3、4、5、6的距离，依次向下直至节点6。 执行子函数dijkstra找到节点1到节点4的最短路径并输出
clc;
close all
clear all
a=zeros(6); a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10; a(2,3)=15;
a(2,4)=20;a(2,6)=25; a(3,4)=10;a(3,5)=20; a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(a==0)=inf;
[distance,path]=dijkstra(a,1,4);
p=num2str(path);
sprintf('最短距离为%d\n具体路线为%s。',distance,p)子函数：
function [mydistance,mypath]=dijkstra(a,sb,db);
% 输入：a—邻接矩阵(aij)是指i到j之间的距离，无向矩阵
% sb—起点的标号, db—终点的标号
% 输出：mydistance—短路的距离, mypath—短路的路径
n=size(a,1); %找出节点个数n
visited(1:n)=0; %构建初步的查找矩阵visited，0代表未查找，1代表查找过
distance(1:n)=inf; %保存起点到各顶点的短距离
distance(sb)=0; %从起点sb到起点的距离为0
parent(1:n)=0;
for i=1:n-1 %循环查找n-1次
temp=distance; %将distance中的值赋给temp，避免运算时丢失原值
id1=find(visited==1); %查找已经标号的点
temp(id1)=inf; %已标号点的距离换成无穷
[t,u]=min(temp); %找标号值小的顶点
visited(u)=1; %标记已经标号的顶点
id2=find(visited==0); %查找未标号的顶点
for v=id2
if a(u,v)+distance(u)代码为书中的案例，具体见姜启源. 数学模型(第二版)[M]// 数学模型（第二版）. 高等教育出版社, 1987.